Дисперзија (физика)

Дисперсија светлости, у ширем смислу, јесте зависност оптичких особина једне средине од фреквенције светлости која пролази кроз ту средину, тј. зависност индекса преламања те средине од кружне фреквенције дате светлости.^[1]

У дисперзивној призми, дисперзија материјала (индекс преламања који зависи од таласне дужине) узрокује преламање различитих боја под различитим угловима, раздвајајући белу светлост у спектар.

Компактна флуоресцентна лампа виђена кроз Амицијеву призму

Разлагање светлости призмом.

Крива која показује ту зависност назива се крива дисперсије, у којој интервали и чине област нормалне дисперсије у којој индекс преламања n расте са порастом кружне фреквенције, а интервал II је област аномалне дисперсије у којој индекс преламања са порастом кружне фреквенције опада.

У истој средини, различите монохроматске светлости (тј. монохроматске светлости различитих таласних дужина) имају различите брзине и различите индексе преламања.

Разлагање беле светлости на спектар

Разлагање беле светлости се лако уочава ако се њен сноп усмери на једну од бочних страна тростране стаклене призме (Њутнов оглед). После преламања кроз призму, на заклону се добија спектар дугиних боја (стакло иначе прелама у области нормалне дисперсије, па за већу кружну фреквенцију светлости, односно за њену мању таласну дужину, скретни угао светлости је већи).

Због тога црвена светлост, која има мању фреквенцију, има и мањи скретни угао, обележен са δcr, од љубичасте светлости веће фреквенције, чији је угао скретања обележен са δlj. Ове две боје су граничне боје дисперзионог спектра. Угао између њихових праваца назива се дисперзиони угао D, и он је једнак разлици скретних углова љубичасте и црвене светлости, дакле D = δlj - δlj.

По изразу уа преламање монохроматске светлости кроз танку призму, то је даље D = (nlj - ncr) • α, при чему су nlj и ncr индекси преламања призме за љубичасту и црвену боју, а α је угао призме. Разлика ова два наведена индекса обично се узима као квантитативно обележје дисперсије неке провидне средине. Осим разлагања беле светлости на спектар, могуће је постићи и обрнуту појаву слагања беле светлости од компоненти њеног спектра тако што се друга призма стави иза прве, тако да се налази на путу разложене беле светлости.

Дисперзија вишег реда у широком пропусном опсегу

Када је широк опсег фреквенција (широка ширина опсега) присутан у једном таласном пакету, као што је ултракратки импулс или чирпусан импулс или други облици преноса проширеног спектра, можда неће бити тачно да се дисперзија апроксимира константом преко целог пропусног опсег, а сложенији прорачуни су потребни за израчунавање ефеката као што је ширење импулса.

Конкретно, горе дефинисани параметар дисперзије D се добија из само једног извода групне брзине. Виши деривати су познати као дисперзија вишег реда.^[2][3] Ови појмови су једноставно проширење у Тејлоров ред дисперзионе релације β(ω) средине или таласовода око неке одређене фреквенције. Њихови ефекти се могу израчунати нумеричком проценом Фуријеове трансформације таласног облика, интеграцијом апроксимација омотача вишег реда са спорим варирањем, методом подељених корака (која може користити тачну релацију дисперзије уместо Тејлоровог низа), или директном симулацијом пуних Максвелових једначина уместо приближне једначине омотача.

Генерализована формулација високог реда дисперзије – Лах-Лeгерова оптика

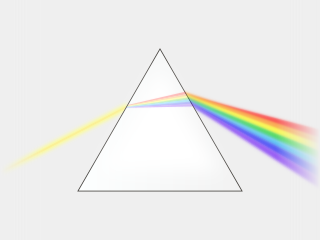
Опис хроматске дисперзије на пертурбативан начин преко Тејлорових коефицијената је повољан за проблеме оптимизације где дисперзију из неколико различитих система треба избалансирати. На пример, код ласерских појачивача са чирпом импулса, импулси се прво растежу у времену помоћу носила да би се избегло оптичко оштећење. Затим у процесу појачања, импулси неизбежно акумулирају линеарну и нелинеарну фазу пролазећи кроз материјале. И на крају, импулси бивају компримовани у разним типовима компресора. Да би ст уклониле сви резидуални виши редови у акумулираној фази, обично се мере и балансирају појединачни редови. Међутим, за униформне системе, такав пертурбативни опис често није потребан (тј. ширење у таласоводима). Редоследи дисперзије су генерализовани на рачунски прихватљив начин, у облику трансформација Лах-Лeгерovog tipa.^[4][5]

Редослед дисперзије је дефинисан Тејлоровом експанзијом фазе или таласног вектора.

${\displaystyle {\begin{array}{c}\varphi \mathrm {(} \omega \mathrm {)} =\varphi \left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial \varphi }{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}\varphi }{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}\varphi }{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}$

${\displaystyle {\begin{array}{c}k\mathrm {(} \omega \mathrm {)} =k\left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial k}{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}k}{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}k}{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}$

The dispersion relations for the wavector ${\displaystyle k\mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}n\mathrm {(} \omega \mathrm {)} }$ and the phase ${\displaystyle \varphi \mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}{\it {OP}}\mathrm {(} \omega \mathrm {)} }$ can be expressed as:

${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}k\mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}n\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}n\mathrm {(} \omega \mathrm {)} \right)\ \end{array}}}$, ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}\varphi \mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} \right)\end{array}}(1)}$

Релације дисперзије за таласни талас ${\displaystyle f\mathrm {(} \omega \mathrm {|} \lambda \mathrm {)} }$ у простору таласне дужине и фреквенције је специфицирана путем Лахове трансформације као:

${\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}$ ${\displaystyle ,}$ ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}(2)}$

Матрични елементи трансформације су Лахови коефицијенти: ${\displaystyle {\mathcal {A}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {1)!} }{\mathrm {(} m\mathrm {-} \mathrm {1)!} }}}$

Написан за GGD, горњи израз налаже да ће константа са таласном дужином GGD, имати нула виших редова. Виши редови који се процењују из GGD су: ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}GDD\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}GDD\mathrm {(} \lambda \mathrm {)} }\end{array}}}$

Замена једначина (2) изражена за индекс преламања ${\displaystyle n}$ или оптички пут ${\displaystyle OP}$ у једначину (1) резултира изразима затвореног облика за редослед дисперзије. Генерално, ${\displaystyle p^{th}}$ ред дисперзије POD је Легеров тип трансформације од негативног реда два:

${\displaystyle POD={\frac {d^{m}\varphi (\omega )}{d\omega ^{m}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}OP(\lambda )}{d\lambda ^{m}}}}$ ${\displaystyle ,}$ ${\displaystyle POD={\frac {d^{m}k(\omega )}{d\omega ^{m}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}n(\lambda )}{d\lambda ^{m}}}}$

Матрични елементи трансформација су неозначени Лагерови коефицијенти реда минус 2 и дати су као: ${\displaystyle {\mathcal {B}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {2)!} }{\mathrm {(} m\mathrm {-} \mathrm {2)!} }}}$

Првих десет редова дисперзије, експлицитно написаних за таласни вектор, су:

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {GD}}}={\frac {\partial }{\partial \omega }}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \omega \mathrm {)} +\omega {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \lambda \mathrm {)} -\lambda {\frac {\partial n\mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\right)=v_{gr}^{\mathrm {-} \mathrm {1} }\end{array}}}$

Групни индекс преламања ${\displaystyle n_{g}}$ је дефинисан као: ${\displaystyle n_{g}=cv_{gr}^{\mathrm {-} \mathrm {1} }}$.

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {GDD}}}={\frac {{\partial }^{2}}{\partial {\omega }^{\mathrm {2} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {2} {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}+\omega {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}\right)={\frac {\mathrm {1} }{c}}\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)\left({\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {TOD}}}={\frac {{\partial }^{3}}{\partial {\omega }^{\mathrm {3} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {3} {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}+\omega {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }{\Bigl (}\mathrm {3} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {FOD}}}={\frac {{\partial }^{4}}{\partial {\omega }^{\mathrm {4} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {4} {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}+\omega {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }{\Bigl (}\mathrm {12} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {8} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {FiOD}}}={\frac {{\partial }^{5}}{\partial {\omega }^{\mathrm {5} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {5} {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}+\omega {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {60} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {60} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {15} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {SiOD}}}={\frac {{\partial }^{6}}{\partial {\omega }^{\mathrm {6} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {6} {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}+\omega {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {360} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {480} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {180} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {24} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+{\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {SeOD}}}={\frac {{\partial }^{7}}{\partial {\omega }^{\mathrm {7} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {7} {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {6} }}}+\omega {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {2520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {2100} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {420} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {35} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {EOD}}}={\frac {{\partial }^{8}}{\partial {\omega }^{\mathrm {8} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {8} {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}+\omega {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {20160} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {40320} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {25200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {6720} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {840} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {48} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+{\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {NOD}}}={\frac {{\partial }^{9}}{\partial {\omega }^{\mathrm {9} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {9} {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}+\omega {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {181440} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {423360} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {317520} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {105840} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {17640} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {1512} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {63} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\boldsymbol {\it {TeOD}}}={\frac {{\partial }^{10}}{\partial {\omega }^{\mathrm {10} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {10} {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}+\omega {\frac {{\partial }^{10}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {1814400} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4838400} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4233600} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{1693440}{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\\+\mathrm {352800} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {40320} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {2520} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {80} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}$

Експлицитно, написано за фазу ${\displaystyle \varphi }$, првих десет редова дисперзије може се изразити као функција таласне дужине користећи Лахову трансформацију (једначина (2)) као:

${\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}$ ${\displaystyle ,}$ ${\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}={-}\left({\frac {\mathrm {2} \pi c}{{\omega }^{\mathrm {2} }}}\right){\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \lambda }}={-}\left({\frac {{\lambda }^{\mathrm {2} }}{\mathrm {2} \pi c}}\right){\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{2}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}={\frac {\partial }{\partial \omega }}\left({\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }\left(\mathrm {2} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+{\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{3}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }\left(\mathrm {6} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {6} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}\right)\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{4}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {24} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {36} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{\mathrm {5} }\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {120} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {240} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {20} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{6}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {720} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1800} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {300} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {30} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}\mathrm {\ +} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{7}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {7} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {5040} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {15120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12600} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {630} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {42} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{8}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {40320} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {141120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {141120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {58800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {11760} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {1176} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {56} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\\+{\lambda }^{\mathrm {8} }{\frac {\partial ^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}$ ${\displaystyle {\begin{array}{l}{\frac {{\partial }^{9}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {362880} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1451520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1693440} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {846720} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {211680} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {28224} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {2016} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {72} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {\partial ^{\mathrm {9} }\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}$

${\displaystyle {\begin{array}{l}{\frac {{\partial }^{10}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {10} }{\Bigl (}\mathrm {3628800} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {16329600} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {21772800} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {12700800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {3810240} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {635040} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {60480} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {3240} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {90} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}$

Референце

1. Born, Max; Wolf, Emil (октобар 1999). Principles of Optics. Cambridge: Cambridge University Press. стр. 14–24. ISBN 0-521-64222-1.CS1 одржавање: Формат датума (веза)
2. Chromatic Dispersion, Encyclopedia of Laser Physics and Technology (Wiley, 2008).
3. Mai, Wending; Campbell, Sawyer D.; Whiting, Eric B.; Kang, Lei; Werner, Pingjuan L.; Chen, Yifan; Werner, Douglas H. (2020-10-01). „Prismatic discontinuous Galerkin time domain method with an integrated generalized dispersion model for efficient optical metasurface analysis”. Optical Materials Express (на језику: енглески). 10 (10): 2542—2559. Bibcode:2020OMExp..10.2542M. ISSN 2159-3930. doi:10.1364/OME.399414 .
4. Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (2022-10-24). „Analytical Lah-Laguerre optical formalism for perturbative chromatic dispersion”. Optics Express (на језику: енглески). 30 (22): 40779—40808. Bibcode:2022OExpr..3040779P. doi:10.1364/OE.457139 .CS1 одржавање: Датум и година (веза)
5. Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (2020-08-30). „Theory of the Chromatic Dispersion, Revisited”. arXiv (на језику: енглески). Bibcode:2020arXiv201100066P. doi:10.48550/ARXIV.2011.00066 .

Спољашње везе

• Дисперсија
• О дисперсији