Funksioni i anasjelltë

Në matematikë, funksioni i anasjelltë i një funksioni ${\displaystyle f}$ (i quajtur edhe inversi i ${\displaystyle f}$ ) është një funksion që zhbën veprimin e ${\displaystyle f}$ . Inversi i ${\displaystyle f}$ ekziston nëse dhe vetëm nëse ${\displaystyle f}$ është bijektiv, dhe nëse ekziston, shënohet me ${\displaystyle f^{-1}.}$

Një funksion ${\displaystyle f}$ dhe inversi i tij ${\displaystyle f^{-1}}$ . Për shkak se ${\displaystyle f}$ pasqyron a në 3, inversi ${\displaystyle f^{-1}}$ e paraqet 3 në a .

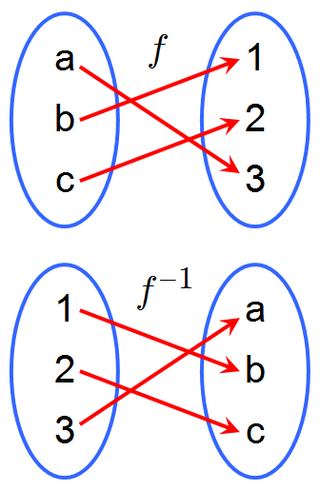
Për një funksion ${\displaystyle f\colon X\to Y}$, e anasjellta e saj ${\displaystyle f^{-1}\colon Y\to X}$ pranon një përshkrim të qartë: ai dërgon çdo element ${\displaystyle y\in Y}$ tek elementi unik ${\displaystyle x\in X}$ e tillë që ${\displaystyle f(x)=y}$ .

Si shembull, merrni parasysh funksionin me vlerë reale të një ndryshoreje reale të dhënë nga ${\displaystyle f(x)=5x-7}$ . Mund të mendohet ${\displaystyle f}$ si funksioni i cili shumëzon hyrjen e tij (${\displaystyle x}$)me 5 dhe më pas zbret 7 nga rezultati. Për ta zhbërë këtë, shtohet 7 në hyrje, pastaj rezultati pjesëtohet me 5. Prandaj, inversi i ${\displaystyle f}$ është funksioni ${\displaystyle f^{-1}\colon \mathbb {R} \to \mathbb {R} }$ përcaktuar nga ${\displaystyle f^{-1}(y)={\frac {y+7}{5}}.}$

Përkufizimet

Nëse ${\displaystyle f}$ hartëzon ${\displaystyle X}$ në ${\displaystyle Y}$, atëherë ${\displaystyle f^{-1}}$ hartëzon ${\displaystyle Y}$ përsëri në ${\displaystyle X}$ .

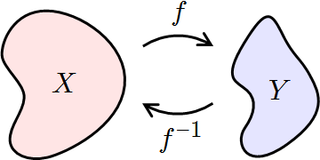
Le të jetë ${\displaystyle f}$ një funksion domeni i të cilit është bashkësia ${\displaystyle X}$ dhe kodomani i të cilit është bashkësia ${\displaystyle Y}$ . Atëherë ${\displaystyle f}$ është i kthyeshëm nëse ekziston një funksion ${\displaystyle g}$ nga ${\displaystyle Y}$ në X i tillë që ${\displaystyle g(f(x))=x}$ per te gjithe ${\displaystyle x\in X}$ dhe ${\displaystyle f(g(y))=y}$ për të gjitha ${\displaystyle y\in Y}$ . ^[1]

Nëse ${\displaystyle f}$ është i kthyeshëm, atëherë ekziston saktësisht një funksion ${\displaystyle g}$ që plotëson këtë veti. Funksioni ${\displaystyle g}$ quhet inversi i ${\displaystyle f}$, dhe zakonisht shënohet si ${\displaystyle f^{-1}}$, një shënim i prezantuar nga John Frederick William Herschel në 1813.

Funksioni f është i kthyeshëm nëse dhe vetëm nëse është bijektiv. Kjo për shkak se kushti ${\displaystyle g(f(x))=x}$ për të gjitha ${\displaystyle x\in X}$ nënkupton që ${\displaystyle f}$ është injektiv, dhe kushti ${\displaystyle f(g(y))=y}$ për të gjitha ${\displaystyle y\in Y}$ do të thotë se ${\displaystyle f}$ është syrjektiv .

Funksioni i anasjelltë f −1 në f mund të përshkruhet në mënyrë eksplicite si funksion

${\displaystyle f^{-1}(y)=({\text{elementi unik }}x\in X{\text{ i tillë që }}f(x)=y)}$ .

I anasjellti dhe përbërja

Kujtoni se nëse ${\displaystyle f}$ është një funksion i kthyeshëm me fytyrë ${\displaystyle X}$ dhe shëmbëllim ${\displaystyle Y}$, atëherë

${\displaystyle f^{-1}\left(f(x)\right)=x}$, për çdo ${\displaystyle x\in X}$ dhe ${\displaystyle f\left(f^{-1}(y)\right)=y}$ për çdo ${\displaystyle y\in Y}$ .

Duke përdorur përbërjen e funksioneve, kjo shpallje mund të rishkruhet në ekuacionet e mëposhtme midis funksioneve:

${\displaystyle f^{-1}\circ f=\operatorname {id} _{X}}$ dhe ${\displaystyle f\circ f^{-1}=\operatorname {id} _{Y},}$