From Wikipedia, the free encyclopedia
සාපේක්ෂතා වාදය (ඉංග්රීසි: Theory of Relativity) යනු ඇල්බට් අයින්ස්ටයින් විසින් හඳුන්වාදුන් භෞතික විද්යාව හා බැඳි න්යායකි. සාපේක්ෂතා න්යායට ඇල්බට් අයින්ස්ටයින් විසින් පිළිවෙලින් 1905 දී සහ 1915 දී ඉදිරිපත් කෙරුණු සාමාන්ය සාපේක්ෂතාවාදය සහ විශේෂ සාපේක්ෂතාවාදය යන සිද්ධාන්ත දෙක ඇතුළත් ය.

20 වෙනි ශතවර්ෂයේ දී සෛද්ධාන්තික භෞතික විද්යාව සහ තාරකා විද්යාව යන ක්ෂේත්ර වල විප්ලවීය වෙනසක් සිදු කිරීමට සාපේක්ෂතාවාදයට හැකි විය. සාපේක්ෂතාවාදය මගින් චතුර්මාන කාල අවකාශය, සමකාලිකතා සාපේක්ෂතාව, ප්රගතික සහ ගුරුත්වජ කාල විස්තාරණය, සහ දිගෙහි සංකෝචනය වැනි සංකල්ප ඉදිරිපත් කරනු ලැබීය. භෞතික විද්යා ක්ෂේත්රයේදී, මූලික අංශු සහ ඒවායේ මූලික අන්තර්ක්රියා ගැන දැනුම වැඩි දියුණු කිරීමට සාපේක්ෂතාවාදය උපකාරී වූ අතර න්යෂ්ටික යුගයට මග පාදන ලදී. සාපේක්ෂතාවාදය භාවිතයෙන් නියුට්රෝන තාරකා, කළු කුහර සහ ගුරුත්වාකර්ෂණ තරංග වැනි තාරකා විද්යාත්මක සංසිද්ධීන් පුරෝකථනය කිරීමට හැකියාව ලැබිණි.
විශේෂ සාපේක්ෂතාවාදය මුලින්ම යෝජනා කළේ ඇල්බට් අයින්ස්ටයින් විසින් 1905 සැප්තැම්බර් 26 දින ප්රකාශයට පත් කරන ලද පත්රිකාවක "චලනය වන ශරීරවල විද්යුත් ගතික විද්යාව" යන මාතෘකාව යටතේ ය. නිව්ටෝනියානු යාන්ත්ර විද්යාවේ මැක්ස්වෙල්ගේ විද්යුත් චුම්භක සමීකරණ සහ පර්යේෂණාත්මකව මයිකල්සන්-මොර්ලි ප්රතිඵලය. (සහ පසුකාලීන සමාන අත්හදා බැලීම්) පෙන්නුම් කළේ ඓතිහාසිකව උපකල්පනය කරන ලද ආලෝකවාහක ඊතරය නොපවතින බවයි. මෙය අයින්ස්ටයින්ගේ විශේෂ සාපේක්ෂතාවාදයේ වර්ධනයට හේතු වූ අතර, සියලු චලිතයන් සහ විශේෂයෙන්ම ආලෝකයට ආසන්න වේගයකින් (සාපේක්ෂතාවාදී ප්රවේග ලෙස හඳුන්වන) තත්වයන් හැසිරවීමට යාන්ත්ර විද්යාව නිවැරදි කරයි. ගුරුත්වාකර්ෂණ සහ ක්වොන්ටම් ආචරණ නොසැලකිලිමත් වන විට ඕනෑම වේගයකින් චලනය වන වඩාත් නිවැරදි ආකෘතිය විශේෂ සාපේක්ෂතාවාදය බව අද ඔප්පු වී ඇත. එසේ වුවද, නිව්ටෝනියානු ආකෘතිය තවමත් අඩු ප්රවේගවලදී (ආලෝකයේ වේගයට සාපේක්ෂව) සරල හා නිවැරදි ආසන්න අගයක් ලෙස වලංගු වේ, උදාහරණයක් ලෙස, පෘථිවියේ එදිනෙදා චලනයන්.
විශේෂ සාපේක්ෂතාවාදයට පර්යේෂණාත්මකව තහවුරු කර ඇති පුළුල් පරාසයක ප්රතිවිපාක ඇත.ඒවාට සමගාමීත්වයේ සාපේක්ෂතාව, දිග හැකිලීම, කාල ප්රසාරණය, සාපේක්ෂතා ප්රවේග එකතු කිරීමේ සූත්රය, සාපේක්ෂතාවාදී ඩොප්ලර් ආචරණය, සාපේක්ෂතාවාදී ස්කන්ධය, විශ්ව වේග සීමාවක්, ස්කන්ධ-ශක්ති සමානාත්මතාවය, හේතුකාරකත්වයේ වේගය සහ තෝමස් පූර්වගාමීත්වය ඇතුළත් වේ. නිදසුනක් වශයෙන්, එය නිරපේක්ෂ විශ්වීය කාලයක් පිළිබඳ සාම්ප්රදායික සංකල්පය සමුද්දේශ රාමුව සහ අවකාශීය පිහිටීම මත රඳා පවතින කාලය පිළිබඳ සංකල්පය සමඟ ප්රතිස්ථාපනය කර ඇත. සිදුවීම් දෙකක් අතර වෙනස් නොවන කාල පරතරයක් වෙනුවට, වෙනස් නොවන අවකාශ කාල පරතරයක් ඇත. භෞතික විද්යාවේ අනෙකුත් නියමයන් සමඟ ඒකාබද්ධව, විශේෂ සාපේක්ෂතාවාදයේ උපකල්පන දෙක ස්කන්ධ සහ ශක්තියේ සමානාත්මතාවය පුරෝකථනය කරයි, {\displaystyle E=mc^{2}}E = mc^2, එහිදී {\ displaystyle c}c යනු රික්තයක ආලෝකයේ වේගයයි. විදුලිය හා චුම්භකත්වයේ සංසිද්ධි සම්බන්ධ වන ආකාරය ද එය පැහැදිලි කරයි.විශේෂ සාපේක්ෂතාවාදයේ නිර්වචන ලක්ෂණයක් වන්නේ නිව්ටෝනියානු යාන්ත්ර විද්යාවේ ගැලීලියානු පරිවර්තන ලොරෙන්ට්ස් පරිවර්තන සමඟ ප්රතිස්ථාපනය කිරීමයි. කාලය සහ අවකාශය එකිනෙක වෙන් වෙන්ව නිර්වචනය කළ නොහැක (කලින් සිතූ පරිදි). ඒ වෙනුවට, අවකාශය සහ කාලය "අවකාශ කාලය" ලෙසින් හැඳින්වෙන තනි සන්තතියකට බැඳී ඇත. එක් නිරීක්ෂකයෙකුට එකවර සිදුවන සිදුවීම් තවත් කෙනෙකුට විවිධ කාලවලදී සිදු විය හැක.
වසර කිහිපයකට පසු අයින්ස්ටයින් ගුරුත්වාකර්ෂණය ඇතුළත් කිරීම සඳහා වක්ර අවකාශ කාලයක් හඳුන්වා දුන් සාමාන්ය සාපේක්ෂතාවාදය වර්ධනය කරන තුරු "විශේෂ සාපේක්ෂතාවාදය" යන වාක්ය ඛණ්ඩය භාවිතා නොකළේය. සමහර විට භාවිතා කරන පරිවර්තනයක් "සීමිත සාපේක්ෂතාවාදය"; "විශේෂ" යනු සැබවින්ම "විශේෂ අවස්ථාව" යන්නයි. න්යාය 1907 දී අත්යවශ්යයෙන්ම සම්පූර්ණ විය.
න්යාය "විශේෂිත" වන්නේ එය අභ්යවකාශ කාලය "පැතලි" වන විශේෂ අවස්ථාවකදී පමණක් වන අතර, එනම් අවකාශ කාලයේ වක්රය (ශක්ති ගම්යතා ආතන්යයේ ප්රතිඵලයක් සහ ගුරුත්වාකර්ෂණය නියෝජනය කරන) නොසැලකිය හැකි අවස්ථාවන්හිදී පමණක් අදාළ වේ. ගුරුත්වාකර්ෂණය නිවැරදිව ඇතුළත් කිරීම සඳහා අයින්ස්ටයින් විසින් 1915 දී සාමාන්ය සාපේක්ෂතාවාදය සකස් කරන ලදී. සමහර ඓතිහාසික විස්තර වලට පටහැනිව විශේෂ සාපේක්ෂතාවාදය ත්වරණයට මෙන්ම ත්වරණය කරන සමුද්දේශ රාමු වලටද ඉඩ සලසයි.
ගැලීලියානු සාපේක්ෂතාවාදය අඩු වේගයන් සඳහා වලංගු වන විශේෂ සාපේක්ෂතාවාදයේ ආසන්න කිරීමක් ලෙස දැන් පිළිගෙන ඇති ආකාරයටම, විශේෂ සාපේක්ෂතාවාදය දුර්වල ගුරුත්වාකර්ෂණ ක්ෂේත්ර සඳහා වලංගු වන සාමාන්ය සාපේක්ෂතාවාදයේ ආසන්න කිරීමක් ලෙස සැලකේ, එනම් ප්රමාණවත් තරම් කුඩා පරිමාණයකින් (උදා. උදම් බලවේග නොසැලකිය හැකිය) සහ නිදහස් වැටීමේ තත්වයන් තුළ. කෙසේ වෙතත්, සාමාන්ය සාපේක්ෂතාවාදය, අවකාශ කාලයේ ජ්යාමිතික වක්රය ලෙස ගුරුත්වාකර්ෂණ බලපෑම් නිරූපණය කිරීම සඳහා යුක්ලීඩීය නොවන ජ්යාමිතිය ඇතුළත් කරයි. විශේෂ සාපේක්ෂතාවාදය මින්කොව්ස්කි අවකාශය ලෙස හඳුන්වන පැතලි අවකාශ කාලයට සීමා වේ. විශ්වය ව්යාජ-රීමානියානු බහුවිධයක් ලෙස ආකෘතිගත කළ හැකි තාක් කල්, මෙම වක්ර අවකාශ කාලය තුළ එක් එක් ලක්ෂ්යයේ ප්රමාණවත් තරම් කුඩා අසල්වැසි ප්රදේශයක් සඳහා විශේෂ සාපේක්ෂතාවාදයට අනුකූල වන Lorentz-අනවශ්ය රාමුවක් අර්ථ දැක්විය හැක.
ගැලීලියෝ ගැලීලි දැනටමත් නිරපේක්ෂ සහ හොඳින් නිර්වචනය කරන ලද විවේකයක් නොමැති බව (වරප්රසාදිත සමුද්දේශ රාමු නොමැත), එය දැන් ගැලීලියෝගේ සාපේක්ෂතා මූලධර්මය ලෙස හැඳින්වේ. අයින්ස්ටයින් මෙම මූලධර්මය දිගු කළ අතර එය ආලෝකයේ නියත වේගය සඳහා හේතු විය,එය මයිකල්සන්-මෝර්ලි අත්හදා බැලීමේදී නිරීක්ෂණය කරන ලද සංසිද්ධියකි. එය යාන්ත්ර විද්යාවේ සහ විද්යුත් ගති විද්යාවේ නීති දෙකම ඇතුළුව භෞතික විද්යාවේ සියලුම නීති සඳහා පවතින බව ද ඔහු උපකල්පනය කළේය.
යාන්ත්ර විද්යාවේ හෝ විද්යුත් ගති විද්යාවේ (එවකට) දන්නා නීතිවල නිශ්චිත වලංගුභාවය කුමක් වුවත්, අයින්ස්ටයින් වඩාත් සහතික වූ බව පෙනෙන මූලික ප්රස්තුත දෙකක් හඳුනා ගත්තේය. මෙම ප්රස්තුතයන් වූයේ රික්තයක ආලෝකයේ වේගයේ අස්ථායීතාවය සහ අවස්ථිති පද්ධතිය තෝරා ගැනීමෙන් භෞතික නීතිවල (විශේෂයෙන් ආලෝකයේ වේගයේ ස්ථාවරත්වය) ස්වාධීනත්වයයි. 1905 දී විශේෂ සාපේක්ෂතාවාදය පිළිබඳ ඔහුගේ මූලික ඉදිරිපත් කිරීමේදී ඔහු මෙම උපකල්පන ප්රකාශ කළේ:
ආලෝකයේ වේගයේ ස්ථාවරත්වය මැක්ස්වෙල්ගේ විද්යුත් චුම්භක න්යාය [උපුටා දැක්වීම අවශ්ය] සහ ලුමිනිෆරස් ඊතර් සඳහා සාක්ෂි නොමැතිකම මගින් පෙලඹී ඇත. මයිකල්සන්-මෝර්ලි අත්හදා බැලීමේ ශූන්ය ප්රතිඵලය අයින්ස්ටයින්ට කෙතරම් බලපෑමක් ඇති කළේද යන්න පිළිබඳ පරස්පර සාක්ෂි තිබේ.කෙසේ වෙතත්, මයිකල්සන්-මෝර්ලි අත්හදා බැලීමේ ශුන්ය ප්රතිඵලය ආලෝකයේ වේගයේ ස්ථාවරත්වය පිළිබඳ සංකල්පය පුළුල්ව පැතිරී ශීඝ්ර ලෙස පිළිගැනීමට උපකාර විය.විශේෂ සාපේක්ෂතාවාදයේ ව්යුත්පන්නය මෙම පැහැදිලි උපකල්පන දෙක මත පමණක් නොව, අභ්යවකාශයේ සමස්ථානික සහ සමජාතීයතාවය සහ ඒවායේ අතීත ඉතිහාසයෙන් මිණුම් දඬු සහ ඔරලෝසු වල ස්වාධීනත්වය ඇතුළුව නිශ්ශබ්ද උපකල්පන කිහිපයක් (භෞතික විද්යාවේ සෑම න්යායකම පාහේ සෑදී ඇත) මත ද රඳා පවතී. [පි 6]
1905 දී අයින්ස්ටයින් විසින් විශේෂ සාපේක්ෂතාවාදය පිළිබඳ මුල් ඉදිරිපත් කිරීමෙන් පසුව, විවිධ විකල්ප ව්යුත්පන්නයන් තුළ විවිධ උපකල්පන මාලාවන් යෝජනා කර ඇත. කෙසේ වෙතත්, වඩාත් පොදු උපකල්පන කට්ටලය අයින්ස්ටයින් ඔහුගේ මුල් පත්රිකාවේ භාවිතා කළ ඒවා වේ. පසුව අයින්ස්ටයින් විසින් සිදු කරන ලද සාපේක්ෂතා මූලධර්මය පිළිබඳ වඩාත් ගණිතමය ප්රකාශයක් වන අතර එය ඉහත සඳහන් නොකළ සරලත්වය පිළිබඳ සංකල්පය හඳුන්වා දෙයි:
සාපේක්ෂතාවාදයේ විශේෂ මූලධර්මය: K ඛණ්ඩාංක පද්ධතියක් තෝරා ගන්නේ නම්, එයට සාපේක්ෂව භෞතික නීති ඒවායේ සරලම ආකාරයෙන් හොඳින් පවතිනු ඇත, එම නීති K′ වෙනත් ඕනෑම ඛණ්ඩාංක පද්ධතියකට සාපේක්ෂව යහපත් වේ k වෙත.
Henri Poincaré විසින් Lorentz පරිවර්තන ඔහුගේ Poincaré සමමිතික පරිවර්තන සමූහයේ උප කුලකයක් බව ඔප්පු කරමින් සාපේක්ෂතා න්යාය සඳහා ගණිතමය රාමුව සැපයීය. අයින්ස්ටයින් පසුව මෙම පරිවර්තනයන් ඔහුගේ ප්රත්යක්ෂ වලින් ලබා ගත්තේය.
අයින්ස්ටයින්ගේ බොහෝ ලිපි ලේඛන මෙම මූලධර්ම දෙක මත පදනම්ව Lorentz පරිවර්තනයේ ව්යුත්පන්නයන් ඉදිරිපත් කරයි.
සමුද්දේශ රාමු සාපේක්ෂතාවාදයේ තීරණාත්මක කාර්යභාරයක් ඉටු කරයි. මෙහි භාවිතා කර ඇති සමුද්දේශ රාමුව යන්න අභ්යවකාශයේ නිරීක්ෂණ ඉදිරිදර්ශනයක් වන අතර එය චලිතයේ (ත්වරණය) කිසිදු වෙනසක් සිදු නොවන අතර, එයින් අවකාශීය අක්ෂ 3ක් (එසේ නම්, විවේකයේදී හෝ නියත ප්රවේගය) ඔස්සේ ස්ථානයක් මැනිය හැක. මීට අමතරව, සමුද්දේශ රාමුවකට 'ඔරලෝසුවක්' (ඒකාකාරී ආවර්තිතා සහිත ඕනෑම සමුද්දේශ උපාංගයක්) භාවිතයෙන් සිදුවීම්වල කාලය මැනීමේ හැකියාව ඇත.
සිදුවීමක් යනු සමුද්දේශ රාමුවකට සාපේක්ෂව අභ්යවකාශයේ තනි අද්විතීය මොහොතක් සහ ස්ථානයක් පැවරිය හැකි සිදුවීමකි: එය අවකාශ කාලයේ "ලක්ෂ්යයක්" වේ. සමුද්දේශ රාමුව නොතකා සාපේක්ෂතාවාදයේ දී ආලෝකයේ වේගය නියත බැවින්, ආලෝකයේ ස්පන්දන මගින් දුර මැනීමට සහ සිදුවීමෙන් පසු ඔරලෝසුව වෙත ළඟා වීමට කාලය ගත වුවද, ඔරලෝසුවට සිදුවීම් සිදු වූ වේලාවන් වෙත ආපසු යොමු කිරීමට ආලෝකයේ ස්පන්දන භාවිතා කළ හැකිය. සිදුවී ඇත.
උදාහරණයක් ලෙස, රතිඤ්ඤා පිපිරවීම "සිදුවීමක්" ලෙස සැලකිය හැකිය. අපට සිදුවීමක් එහි අවකාශ කාල ඛණ්ඩාංක හතරකින් සම්පූර්ණයෙන්ම සඳහන් කළ හැක: සිදුවීමේ වේලාව සහ එහි ත්රිමාන අවකාශීය පිහිටීම යොමු ලක්ෂ්යයක් නිර්වචනය කරයි. අපි මෙම සමුද්දේශ රාමුව S ලෙස හඳුන්වමු.
සාපේක්ෂතා න්යායේ දී, අපට බොහෝ විට අවශ්ය වන්නේ සිදුවීමක ඛණ්ඩාංක විවිධ සමුද්දේශ රාමු වලින් ගණනය කිරීමට ය. විවිධ රාමු වලින් සාදන ලද මිනුම් සම්බන්ධ කරන සමීකරණ පරිවර්තන සමීකරණ ලෙස හැඳින්වේ.
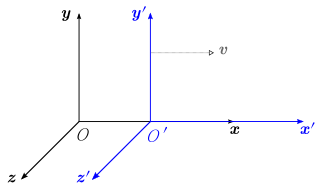
විවිධ සමුද්දේශ රාමු තුළ නිරීක්ෂකයින් විසින් මනිනු ලබන අවකාශ කාල ඛණ්ඩාංක එකිනෙක හා සසඳන ආකාරය පිළිබඳ අවබෝධයක් ලබා ගැනීමට, සම්මත වින්යාසය තුළ රාමු සහිත සරල සැකසුමකින් වැඩ කිරීම ප්රයෝජනවත් වේ. මෙය ගණිතය සරල කිරීමට ඉඩ සලසයි. එළඹෙන නිගමනවල සාමාන්යභාවය නැතිවීමකින් තොරව. රූපය 2-1 හි, ගැලීලියානු සමුද්දේශ රාමු දෙකක් (එනම්, සම්ප්රදායික 3-අවකාශ රාමු) සාපේක්ෂ චලිතයෙන් ප්රදර්ශනය කෙරේ. S රාමුව O පළමු නිරීක්ෂකයෙකුට අයත් වන අතර රාමුව S′ ("S ප්රයිම්" හෝ "S dash" ලෙස උච්චාරණය කෙරේ) දෙවන නිරීක්ෂක O ට අයත් වේ.
සාපේක්ෂතාවාදයේ නිරපේක්ෂ සමුද්දේශ රාමුවක් නොමැති බැවින්, වෙනත් සමුද්දේශ රාමුවකට අදාළව සියල්ල චලනය විය හැකි බැවින්, 'චලනය' යන සංකල්පය දැඩි ලෙස නොපවතී. ඒ වෙනුවට, එකම දිශාවකට එකම වේගයකින් චලනය වන ඕනෑම රාමු දෙකක් චලනය වන බව කියනු ලැබේ. එම නිසා, S සහ S′ සංකෝචනය නොවේ.
එක් එක් අවස්ථිති සමුද්දේශ රාමුව තුළ භෞතික නීති එකම ස්වරූපයක් ඇති බව පවසන සාපේක්ෂතාවාදයේ මූලධර්මය ගැලීලියෝ දක්වා දිවෙන අතර එය නිව්ටෝනීය භෞතික විද්යාවට ඇතුළත් විය. කෙසේ වෙතත්, 19 වන ශතවර්ෂයේ අගභාගයේදී, විද්යුත් චුම්භක තරංගවල පැවැත්ම සමහර භෞතික විද්යාඥයින් විසින් විශ්වය ඔවුන් විසින් හඳුන්වනු ලබන "ඊතර්" නම් ද්රව්යයකින් පුරවා ඇති බවට යෝජනා කිරීමට හේතු විය, ඔවුන් අනුමාන කළේ, මෙම තරංග හෝ කම්පන මාධ්ය ලෙස ක්රියා කරන බවයි. ප්රචාරණය (බොහෝ පැතිවලින් වාතය හරහා ශබ්දය ප්රචාරණය වන ආකාරයට සමාන). ඊතර් යනු සියලු වේගයන් මැනිය හැකි නිරපේක්ෂ සමුද්දේශ රාමුවක් ලෙස සලකනු ලැබූ අතර, පෘථිවියට හෝ වෙනත් ස්ථාවර යොමු ලක්ෂ්යයකට සාපේක්ෂව ස්ථාවර සහ චලනය නොවන ලෙස සැලකිය හැකිය. ඊතර් විද්යුත් චුම්භක තරංගවලට ආධාර කිරීමට ප්රමාණවත් තරම් ප්රත්යාස්ථ විය යුතු අතර, එම තරංගවලට ද්රව්ය සමඟ අන්තර් ක්රියා කළ හැකි වුවද, ඒ හරහා ගමන් කරන සිරුරුවලට කිසිදු ප්රතිරෝධයක් ලබා නොදේ (එහි එක් ගුණාංගයක් වූයේ එය විද්යුත් චුම්භක තරංග ප්රචාරණය කිරීමට ඉඩ දීමයි). 1887 දී Michelson-Morley අත්හදා බැලීම ඇතුළු විවිධ පරීක්ෂණවල ප්රතිඵල (පසුව වඩාත් නිවැරදි හා නව්ය අත්හදා බැලීම් මගින් තහවුරු කරන ලදී), ඊතර් නොපවතින බව පෙන්වීමෙන් විශේෂ සාපේක්ෂතාවාදයේ න්යාය වෙත යොමු විය. අයින්ස්ටයින්ගේ විසඳුම වූයේ ඊතර් සහ නිරපේක්ෂ විවේක තත්ත්වය පිළිබඳ සංකල්පය ඉවත දැමීමයි. සාපේක්ෂතාවාදයේ දී, ඒකාකාර චලිතයකින් චලනය වන ඕනෑම සමුද්දේශ රාමුවක් භෞතික විද්යාවේ එකම නියමයන් නිරීක්ෂණය කරයි. විශේෂයෙන්ම, විවිධ (නමුත් නියත) ප්රවේගවලින් චලනය වන බහු පද්ධති මගින් මනින විට පවා රික්තයේ ආලෝකයේ වේගය සෑම විටම c ලෙස මනිනු ලැබේ.
ආලෝකයේ ප්රවේගයේ නියතතාව උපකල්පනය නොකර සාපේක්ෂතාවාදයේ මූලධර්මයෙන් පමණක් (එනම්, අවකාශයේ සමස්ථානිකය සහ විශේෂ සාපේක්ෂතා මූලධර්මය මගින් ගම්ය වන සමමිතිය භාවිතා කරමින්) අවස්ථිති රාමු අතර අවකාශ කාල පරිවර්තන යුක්ලීඩීය, ගැලීලියන් බව පෙන්විය හැක. , හෝ Lorentzian. Lorentzian නඩුවේදී, කෙනෙකුට පසුව සාපේක්ෂතාවාදී විරාම සංරක්ෂණය සහ යම් සීමිත සීමාකාරී වේගයක් ලබා ගත හැක. මෙම වේගය රික්තය තුළ ආලෝකයේ වේගය බව අත්හදා බැලීම් යෝජනා කරයි
ප්රධාන ලිපිය: Lorentz පරිවර්තනය
අයින්ස්ටයින් ලොරෙන්ට්ස් විචල්යතාවයේ ව්යුත්පන්නය (විශේෂ සාපේක්ෂතාවාදයේ අත්යාවශ්ය හරය) පදනම් වූයේ සාපේක්ෂතාවාදය සහ සැහැල්ලු වේග විචලනය යන මූලික මූලධර්ම දෙක මත පමණි. (ඔහු ලිව්ව)
විශේෂ සාපේක්ෂ න්යාය සඳහා වන තීක්ෂ්ණ බුද්ධිය මෙයයි: ඛණ්ඩාංක සහ සිදුවීම් කාල පරිවර්ථනය සඳහා නව වර්ගයක ("ලෝරෙන්ට්ස් පරිවර්තනය") සම්බන්ධතා උපකල්පනය කරන්නේ නම්, උපකල්පන සාපේක්ෂතාවාදය සහ සැහැල්ලු වේග විචලනය අනුකූල වේ ... විශ්වීය මූලධර්මය විශේෂ සාපේක්ෂතාවාදයේ න්යාය අනුප්රාප්තියෙහි අන්තර්ගත වේ: Lorentz පරිවර්තන සම්බන්ධයෙන් භෞතික විද්යාවේ නියමයන් වෙනස් නොවේ (එක් අවස්ථිති පද්ධතියක සිට වෙනත් ඕනෑම අත්තනෝමතික ලෙස තෝරාගත් අවස්ථිති පද්ධතියකට සංක්රමණය වීම සඳහා). මෙය ස්වභාවික නීති සඳහා සීමා කිරීමේ මූලධර්මයකි
මේ අනුව විශේෂ සාපේක්ෂතාවාදයේ බොහෝ නවීන ප්රතිකාර එය විශ්වීය ලොරෙන්ට්ස් සහජීවනයේ තනි උපකල්පනය මත පදනම් වේ, නැතහොත්, ඊට සමානව, මින්කොව්ස්කි අවකාශකාලයේ තනි උපකල්පනය මත පදනම් වේ.


විශ්වීය Lorentz covariance ව්යුත්පන්න මූලධර්මයක් ලෙස සලකනවා වෙනුවට, මෙම ලිපිය එය විශේෂ සාපේක්ෂතාවාදයේ මූලික උපකල්පනය ලෙස සලකයි. විශේෂ සාපේක්ෂතාවාදය සඳහා සම්ප්රදායික ද්වි-ස්ථිතික ප්රවේශය අසංඛ්යාත විද්යාල පෙළපොත් සහ ජනප්රිය ඉදිරිපත් කිරීම් වල ඉදිරිපත් කෙරේ. මින්කොව්ස්කි අභ්යවකාශ කාලය පිළිබඳ තනි උපකල්පනයෙන් ආරම්භ වන පෙළපොත් අතර ටේලර් සහ වීලර්සහ කැලහාන් විසින් රචිත ඒවා ඇතුළත් වේ.[22] විකිපීඩියා ලිපි Spacetime සහ Minkowski රූප සටහන අනුගමනය කරන ප්රවේශය ද මෙයයි.
S පද්ධතියේ අවකාශීය ඛණ්ඩාංක (t, x, y, z) සහ (t′, x′, y′, z′) සමුද්දේශ රාමුවක එම රාමුවට සාපේක්ෂව v වේගයකින් චලනය වන සිදුවීමක් නිර්වචනය කරන්න, S′ . එවිට Lorentz පරිවර්තනය මෙම ඛණ්ඩාංක පහත ආකාරයෙන් සම්බන්ධ වන බව සඳහන් කරයි
හී

Lorentz සාධකය වන අතර c යනු රික්තයේ ආලෝකයේ වේගය වන අතර S ට සාපේක්ෂව S′ හි ප්රවේගය v x අක්ෂයට සමාන්තර වේ. සරල බව සඳහා, y සහ z ඛණ්ඩාංක බලපාන්නේ නැත; x සහ t ඛණ්ඩාංක පමණක් පරිවර්තනය වේ. මෙම Lorentz පරිවර්තන රේඛීය සිතියම්කරණ එක් පරාමිති සමූහයක් සාදයි, එම පරාමිතිය වේගවත් බව ලෙස හැඳින්වේ. ප්රාථමික නොවන ඛණ්ඩාංක සඳහා ඉහත පරිවර්තන සමීකරණ හතර විසඳීම ප්රතිලෝම Lorentz පරිවර්තනය ලබා දෙයි

මෙම ප්රතිලෝම Lorentz පරිවර්තනය ප්රාථමිකයේ සිට ප්රාථමික පද්ධතියට Lorentz පරිවර්තනය සමග සමපාත වන පරිදි බලාත්මක කිරීම, ප්රාථමික රාමුවේ මනින ලද පරිදි ප්රාථමික නොවන රාමුව v′ = −v ප්රවේගය සමඟ චලනය වන බව පෙන්වයි.
x අක්ෂය ගැන විශේෂ දෙයක් නැත. පරිවර්තනය y- හෝ z-අක්ෂයට හෝ ඇත්ත වශයෙන්ම චලනයට සමාන්තරව ඕනෑම දිශාවකට (γ සාධකය මගින් විකෘති කරන ලද) සහ ලම්බකව යෙදිය හැක; විස්තර සඳහා Lorentz පරිවර්තනය යන ලිපිය බලන්න.
Lorentz පරිවර්තන යටතේ වෙනස් වන ප්රමාණය Lorentz පරිමාණයක් ලෙස හැඳින්වේ.
Lorentz පරිවර්තනය සහ එහි ප්රතිලෝමය ඛණ්ඩාංක වෙනස්කම් අනුව ලිවීමේදී, එක් සිදුවීමකට ඛණ්ඩාංක (x1, t1) සහ (x′1, t′1) ඇත, තවත් සිදුවීමක ඛණ්ඩාංක (x2, t2) සහ (x′2, t) ඇත. ′2), සහ වෙනස්කම් ලෙස අර්ථ දක්වා ඇත.



Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.