කුලක පිළිබඳ වීජ ගණිතය

කුලක පිළිබඳ වීජ ගණිතය, කුලකවල ගුණ හා නීති නංවමින් පැහැදිලි කරයි. එය කුලක මේලය, ඡේදනය, අනුපූරණය, කුලක සමානතාවයේ සම්බන්ධතා සහ කුලක අන්තර්ගතය පිලිබද සිද්ධාන්තවලින් සමන්විතය. ශ්‍රිතයන් ආදී වන සියළු ගණිතමය වස්තූන් පාහේ අර්ථ දැක්වීමේදී කුලක වාදයේ භාෂා ක්‍රමය භාවිතා වේ. එමඟින් මූලධර්ම ඇගයීම හා ගණනයක් සිදු කිරීම සඳහා ක්‍රමවත් ක්‍රියා පිළිවෙලක් සපයයි.

කුලක දෙකක ඡේදනය

මූලධර්ම

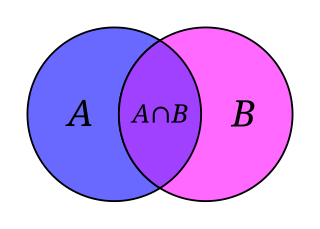
කුලක වීජ ගණිතය යනු සංඛ්‍යාත්මක වීජ ගණිතයේ න්‍යායාත්මක විශ්ලේෂණය වේ. අංක ගණිතයෙහි එකතු කිරීම හා ගුණ කිරීම න්‍යාදේශ හා සංඝටන වන්නාක් මෙන්, කුලක වීජ ගණිතයෙහි කුලක මේලය හා කුලක ඡේදනය එසේ වේ. අංක ගණිතයෙහි කුඩා හෝ සමාන යන්න, කුලක වීජ ගණිතයෙහි උපකුලකයට අනුරූප වේ.

කුලක වීජ ගණි‍තයේ මූලික න්‍යායන්

කුලකයේ ද්වීමය කර්මයන් වන මේලය ${\textstyle (\cup )}$හා ජේදනය ${\textstyle (\cap )}$බොහෝ සර්වසාම්‍යයන් තෘප්ත කරයි. මෙකී සර්වසාම්‍යයන් හෝ ‘න්‍යායන්’ කිහිපයක් සඳහාම ‍විශේෂ වූ නම් ඇත. න්‍යාය යුගල තුනක් සාධනයෙන් තොරව පහත ප්‍රමේය තුළ ප්‍රකාශ වේ.

පළමු ප්‍රමේය - ඕනෑම ${\displaystyle A}$,${\displaystyle B}$ හා ${\displaystyle C}$ කුලක සඳහා පහත සර්වසාම්‍යයන් සත්‍ය වේ.

න්‍යාදේශ න්‍යාය:

• ${\displaystyle A\cup B=B\cup A\,\!}$
• ${\displaystyle A\cap B=B\cap A\,\!}$

සංඝටන න්‍යාය:

• ${\displaystyle (A\cup B)\cup C=A\cup (B\cup C)\,\!}$
• ${\displaystyle (A\cap B)\cap C=A\cap (B\cap C)\,\!}$

විඝටන න්‍යාය:

• ${\displaystyle A\cup (B\cap C)=(A\cup B)\cap (A\cup C)\,\!}$
• ${\displaystyle A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\,\!}$

කුලකවල ජේදනය හා මේලය හා සංඛ්‍යාවල ආකලණය හා ගුණනය අතර ප්‍රතිසමතාව බොහෝ අපූරුය. ආකලණය හා ගුණනය පරිදිම, ජේදනයේ හා මේලයේ කර්මයන් න්‍යායදේශ හා සංඝටනවන අතර ජේදනය මේලයන් විඝටනය වේ. නමුත් ආකලණය හා ගුණනය පරිදි නොව, මේලයද ජේදනයෙන් විඝටනය වේ.

ඊළග ප්‍රමේයෙන්, විශේෂිත කුලක 3 ක් ද සම්බන්ධ තවත් න්‍යාය යුගල දෙකක් ප්‍රකාශ කරයි. ශූන්‍ය කුලකය , සර්වත්‍ර කුලකය හා කුලක අනුපූරකය එම කුලක තුනයි.

දෙවන ප්‍රමේය - ${\displaystyle U}$ සර්වත්‍ර කුලකයේ ඕනෑම ${\displaystyle A}$ උපකුලකයක් සඳහා පහත සර්ව සාමාන්‍යයන් සත්‍ය වේ.

තදාස්ම්‍ය න්‍යාය:

• ${\displaystyle A\cup \varnothing =A\,\!}$
• ${\displaystyle A\cap U=A\,\!}$

අනුපූරක න්‍යාය

• ${\displaystyle A\cup \varnothing =A\,\!}$
• ${\displaystyle A\cap U=A\,\!}$

සර්වසාම්‍ය නියමයන් (න්‍යාදේශ න්‍යායන් සමග) පවසනුයේ, ආකලණය හා ගුණනය සඳහා 0 ‍හා 1 පරිදිම, පිළිවෙලින් ${\textstyle \varnothing }$ හා ${\displaystyle U}$, මේලය හා ජේදනය සඳහා සර්වසාම්‍ය අවයවයන් බවයි.

ආකලණය හා ගුණනය පරිදි නොව මේලය හා ජේදනය සඳහා ප්‍රතිලෝම අවයව නැත. කෙසේ නමුත් අනුපූරක න්‍යායන් අනුපූරණ කුලකයේ, ප්‍රතිලෝමයට තරමක් සමාන ඒකමය කර්මයෙහි මූලික ලක්ෂණ ලබාදෙයි.

ඉහත සඳහන් කළ න්‍යාය යුගල පහ - න්‍යාදේශ, සංඝටන, විඝටන, සර්වසාම්‍ය හා අනුපූරක න්‍යායන්, කුලකවල සියලුම වලංගු ප්‍රමේයන් මගින් ව්‍යුත්පන්න කළ හැකි බැවින් කුලක වීජ ගණිතයේ සියල්ල ඉන් ආවරණය වේ යැයි කිව හැකිය.

කුලක මේලය හා ඡේදනය ආශ්‍රිත තවත් න්‍යායන්

Idempotent laws:

• ${\displaystyle A\cup A=A}$
• ${\displaystyle A\cap A=A}$

Domination laws:

• ${\displaystyle A\cup U=U}$
• ${\displaystyle A\cap \varnothing =\varnothing }$

Absorption laws:

• ${\displaystyle A\cup (A\cap B)=A}$
• ${\displaystyle A\cap (A\cup B)=A}$

කුලක අනුපූරකය ආශ්‍රිත තවත් න්‍යායන්

ඩි මෝගන් න්‍යාය:

• ${\displaystyle (A\cup B)^{/}=A^{/}\cap B^{/}}$
• ${\displaystyle (A\cap B)^{/}=A^{/}\cup B^{/}}$

ද්විත්ව අනුපූරක න්‍යාය:

• ${\displaystyle {(A^{C})}^{C}=A}$

සර්වත්‍ර කුලකය හා අභිශුන්‍ය කුලකය සඳහා අනුපූරක න්‍යාය:

• ${\displaystyle \varnothing ^{C}=U}$
• ${\displaystyle U^{C}=\varnothing }$

මේවාත් බලන්න

• කුලක වාදය
• කුලක වාදයේ මූලික සංකල්ප

බාහිර සබැඳි

• Operations on Sets at ProvenMath