Эффективная площадь рассеяния

Эффекти́вная пло́щадь рассе́яния (ЭПР; в некоторых источниках — эффективная пове́рхность рассеяния, эффективный попере́чник рассеяния, эффективная отража́ющая площадь, ЭОП) в радиолокации — площадь некоторой фиктивной плоской поверхности, расположенной нормально к направлению падающей плоской волны и являющейся идеальным и изотропным переизлучателем, которая, будучи помещена в точку расположения цели, создаёт в месте расположения антенны радиолокационной станции ту же плотность потока мощности, что и реальная цель^[1].

Пример диаграммы моностатической ЭПР (A-26 Инвэйдер)

ЭПР является количественной мерой свойства объекта рассеивать электромагнитную волну^[2]. Наряду с энергетическим потенциалом приемопередающего тракта и КУ антенн РЛС, ЭПР объекта входит в уравнение дальности радиолокации и определяет дальность, на которой объект может быть обнаружен радиолокатором. Повышенное значение ЭПР означает бо́льшую радиолокационную заметность объекта, снижение ЭПР затрудняет обнаружение (см. стелс-технология).

ЭПР конкретного объекта зависит от его формы, размеров, материала, из которого он изготовлен, от его ориентации (ракурса) по отношению к антеннам передающей и приемной позиций РЛС (в том числе, и от поляризации электромагнитных волн), от длины волны зондирующего радиосигнала. ЭПР определяется в условиях дальней зоны рассеивателя, приемной и передающей антенн радиолокатора.

Поскольку ЭПР — формально введенный параметр, то её значение не совпадает ни со значением полной площади поверхности рассеивателя, ни со значением площади его поперечного сечения (англ. Cross-Section). Расчет ЭПР — одна из задач прикладной электродинамики, которая решается с той или иной степенью приближения аналитически (только для ограниченного ассортимента тел простой формы, например, проводящей сферы, цилиндра, тонкой прямоугольной пластины и т. п.) или численными методами. Измерение (контроль) ЭПР проводится на полигонах и в радиочастотных безэховых камерах с использованием реальных объектов и их масштабных моделей.

ЭПР имеет размерность площади и обычно указывается в м² или дБкв.м. Для объектов простой формы — тестовых — ЭПР принято нормировать к квадрату длины волны зондирующего радиосигнала. ЭПР протяженных цилиндрических объектов нормируют к их длине (погонная ЭПР, ЭПР на единицу длины). ЭПР распределенных в объёме объектов (например, дождевого облака) нормируют к объёму элемента разрешения РЛС (ЭПР/м³). ЭПР поверхностных целей (как правило, участка земной поверхности) нормируют к площади элемента разрешения РЛС (ЭПР/м²). Иными словами, ЭПР распределенных объектов зависит от линейных размеров конкретного элемента разрешения конкретной РЛС, которые зависят от расстояния РЛС — объект.

ЭПР можно определить следующим образом (определение эквивалентно приведенному в начале статьи):

Эффективная площадь рассеяния (для гармонического зондирующего радиосигнала) — отношение мощности радиоизлучения эквивалентного изотропного источника (создающего в точке наблюдения такую же плотность потока мощности радиоизлучения, что и облучаемый рассеиватель) к плотности потока мощности (Вт/м²) зондирующего радиоизлучения в точке расположения рассеивателя^[3].

ЭПР зависит от направления от рассеивателя на источник зондирующего радиосигнала и направления в точку наблюдения. Поскольку эти направления могут не совпадать (в общем случае источник зондирующего сигнала и точка регистрации рассеянного поля разнесены в пространстве), то определенная таким образом ЭПР называется бистатической ЭПР (двухпозиционной ЭПР, англ. bistatic RCS).

Диаграмма обратного рассеяния (ДОР, моностатическая ЭПР, однопозиционная ЭПР, англ. monostatic RCS, back-scattering RCS) — значение ЭПР при совпадении направлений от рассеивателя на источник зондирующего сигнала и на точку наблюдения. Под ЭПР часто подразумевают её частный случай — моностатическую ЭПР, то есть ДОР (смешивают понятия ЭПР и ДОР) из-за малой распространенности бистатических (многопозиционных) РЛС (по сравнению с традиционными моностатическими РЛС, оснащенными единой приемо-передающей антенной). Тем не менее, следует различать ЭПР(θ, φ; θ₀, φ₀) и ДОР(θ, φ) = ЭПР(θ, φ; θ₀=θ, φ₀=φ), где θ, φ — направление на точку регистрации рассеянного поля; θ₀, φ₀ — направление на источник зондирующей волны (θ, φ, θ₀, φ₀ — углы сферической системы координат, начало которой совмещено с рассеивателем).

В общем случае для зондирующей электромагнитной волны с негармонической временной зависимостью (широкополосный в пространственно-временно́м смысле зондирующий сигнал) эффективная площадь рассеяния — отношение энергии эквивалентного изотропного источника к плотности потока энергии (Дж/м²) зондирующего радиоизлучения в точке расположения рассеивателя.

Расчёт ЭПР

Рассмотрим отражение волны, падающей на изотропно отражающую поверхность, площадью, равной ЭПР. Отражённая от такой цели мощность — это произведение ЭПР на плотность падающего потока мощности:

${\displaystyle P_{2}=\sigma \cdot \rho _{1}}$,

(1)

где ${\displaystyle \sigma }$ — ЭПР цели, ${\displaystyle \rho _{1}}$ — плотность потока мощности падающей волны данной поляризации в точке расположения цели, ${\displaystyle P_{2}}$ — мощность, отражённая целью.

С другой стороны, излучённая изотропно мощность

${\displaystyle P_{2}=4\pi R^{2}\cdot \rho _{2}}$,

(2)

где ${\displaystyle R}$ — расстояние от РЛС до цели, ${\displaystyle \rho _{2}}$ — плотность потока мощности отражённой от цели волны данной поляризации в точке расположения РЛС.

Подставляя выражение (2) в (1), получаем выражение для ЭПР цели:

${\displaystyle \sigma =4\pi R^{2}{\frac {\rho _{2}}{\rho _{1}}}}$.

(3)

Или, используя напряженности поля падающей волны ${\displaystyle E_{1}}$ в точке нахождения цели и отраженной волны ${\displaystyle E_{2}}$ в месте расположения РЛС:

${\displaystyle \sigma =4\pi R^{2}{\frac {E_{2}^{2}}{E_{1}^{2}}}}$.

(4)

Мощность на входе приёмника:

${\displaystyle P_{r}=\rho _{2}\cdot S_{A}}$,

(5)

где ${\displaystyle S_{A}}$ — эффективная площадь антенны.

Можно определить поток мощности падающей волны через излучённую мощность ${\displaystyle P_{e}}$ и коэффициент направленного действия антенны ${\displaystyle D}$ для данного направления излучения.

${\displaystyle \rho _{1}={\frac {P_{e}}{4\pi R^{2}}}D}$.

(6)

Подставляя (6) и (2) в (5), для мощности на входе приёмника РЛС имеем:

${\displaystyle P_{r}=S_{A}\cdot \rho _{2}=S_{A}{\frac {P_{2}}{4\pi R^{2}}}=S_{A}{\frac {\sigma \rho _{1}}{4\pi R^{2}}}=S_{A}\sigma {\frac {P_{e}}{(4\pi R^{2})^{2}}}D}$.

(7)

Или

${\displaystyle P_{r}=k_{0}\sigma }$,

(8)

где ${\displaystyle k_{0}={\frac {P_{e}}{(4\pi R^{2})^{2}}}DS_{A}}$.

Таким образом,

${\displaystyle \sigma ={\frac {P_{r}}{P_{e}}}{\frac {(4\pi R^{2})^{2}}{S_{A}D}}}$.

(9)

Физический смысл ЭПР

ЭПР имеет размерность площади (м²), но является не геометрической площадью, а энергетической характеристикой, то есть определяет величину мощности принимаемого сигнала.

${\displaystyle \sigma [db]=10\lg {\frac {\sigma }{\sigma _{0}}}}$

Аналитически ЭПР можно рассчитать только для простых целей. Для сложных целей ЭПР измеряется практически на специализированных полигонах, или в безэховых камерах.

ЭПР цели не зависит ни от интенсивности излучаемой волны, ни от расстояния между станцией и целью. Любое увеличение ${\displaystyle \rho _{1}}$ ведёт к пропорциональному увеличению ${\displaystyle \rho _{2}}$ и их отношение в формуле не изменяется. При изменении расстояния между РЛС и целью отношение ${\displaystyle {\rho _{2}}/{\rho _{1}}}$ меняется обратно пропорционально ${\displaystyle R^{2}}$ и величина ЭПР при этом остается неизменной.

ЭПР распространённых точечных целей

Выпуклой поверхности

Поле от всей поверхности S определяется интегралом ${\displaystyle \int \limits _{S}...\,dS}$. Необходимо определить E₂ и отношение ${\displaystyle {\frac {E_{2}^{2}}{E_{1}^{2}}}}$ при заданном расстоянии до цели.

Везде ниже ${\displaystyle {\lambda }}$ означает длину волны в сантиметрах.

${\displaystyle \sigma =4\pi R^{2}\left|{\frac {E_{2}^{2}}{E_{1}^{2}}}\right|}$

${\displaystyle E_{2}={\frac {1}{\lambda }}\int \limits _{S}{\frac {E_{1}}{R}}\exp(-j\cdot 2kR)\cos \theta \,dS}$,

(10)

где k — волновое число.

1) Если объект небольших размеров, то ${\displaystyle R,E_{1}\approx const}$ — расстояние и поле падающей волны можно считать неизменными. 2) Расстояние R можно рассматривать как сумму расстояния до цели и расстояния в пределах цели:

${\displaystyle R=R_{0}+r}$

• ${\displaystyle R_{0}}$ — расстояние от РЛС до объекта
• ${\displaystyle r}$ — местное расстояние

Тогда:

${\displaystyle E_{2}={\frac {E_{1}}{\lambda R}}\exp(-j\cdot 2kR_{0})\int \limits _{S}{\frac {E_{1}}{R}}\exp(-j\cdot 2kr)\cos \theta \,dS}$,	(11)
${\displaystyle {\frac {E_{2}}{E_{1}}}={\frac {1}{\lambda R}}e^{-j2kR}\int \limits _{S}{\frac {E_{1}}{R}}e^{-j2kr}\cos \theta \,dS}$,	(12)
${\displaystyle \left|{\frac {E_{2}}{E_{1}}}\right|=\left|{\frac {1}{\lambda R}}\left(e^{-j4\pi {\frac {R}{\lambda }}}{\Bigr |}_{\approx 1}\right)\int \limits _{S}{\frac {E_{1}}{R}}e^{(-j2kr)}\cos \theta \,dS\right|={\frac {1}{\lambda R}}\left|\int \limits _{S}{\frac {E_{1}}{R}}e^{(-j2kr)}\cos \theta \,dS\right|}$,	(13)
${\displaystyle \sigma ={\frac {4\pi }{\lambda ^{2}}}\left|\int \limits _{S}e^{-j2{\frac {2\pi }{\lambda }}r}\cos \theta \,dS\right|^{2}}$,	(14)

Плоской пластины

Плоская поверхность — частный случай криволинейной выпуклой поверхности.

${\displaystyle \sigma ={\frac {4\pi }{\lambda ^{2}}}S^{2}}$

(15)

Если плоскость с площадью 1 м², а длина волны 10 см (3 ГГц), то

${\displaystyle \sigma ={\frac {4\pi \approx 12}{10^{-2}}}\approx 1200[m^{2}]}$

Шара

Для шара 1-й зоной Френеля будет зона, ограниченная экватором.

${\displaystyle \sigma =\pi r^{2}}$

(16)

Уголкового отражателя

Принцип действия уголкового отражателя

Основная статья: Уголковый отражатель

Уголковый отражатель представляет собой три перпендикулярно расположенных плоскости. В отличие от пластины, уголковый отражатель даёт хорошее отражение в широком диапазоне углов.

Треугольный

Если используется уголковый отражатель с треугольными гранями, то ЭПР

${\displaystyle \sigma ={\frac {4\pi }{3\lambda ^{2}}}a^{4},}$

(17)

где ${\displaystyle a}$ — длина ребра.

Четырёхугольный

Если уголковый отражатель составлен из граней четырёхугольной формы, то ЭПР

${\displaystyle \sigma ={\frac {4\pi }{\lambda ^{2}}}3a^{4}.}$

(18)

Применение уголковых отражателей

Уголковые отражатели применяются:

• в качестве ложных целей;
• как радио-контрастные ориентиры;
• при проведении экспериментов сильного направленного излучения.

Дипольного отражателя

Основная статья: Дипольный отражатель

Дипольные отражатели используются для создания пассивных помех работе РЛС.

Величина ЭПР дипольного отражателя зависит в общем случае от ракурса наблюдения, однако ЭПР по всем ракурсам:

${\displaystyle \sigma =0,17\lambda ^{2}}$

Дипольные отражатели используются для маскировки воздушных целей и рельефа местности, а также как пассивные радиолокационные маяки.

Сектор отражения дипольного отражателя составляет ~70°

ЭПР сложных целей (реальных объектов)

ЭПР сложных реальных объектов измеряются на специальных установках, или полигонах, где достижимы условия дальней зоны облучения.

#	Тип цели	${\displaystyle \sigma _{\text{ц}}}$ [м²]
1	Авиация
1.1	Самолёт-истребитель	3—12[4]
1.2	Малозаметный истребитель	0,3—0,4[4]
1.3	Фронтовой бомбардировщик	7—10
1.4	Тяжёлый бомбардировщик	13—20
1.4.1	Бомбардировщик В-52	100[5]
1.4	Транспортный самолёт	40—70
2	Суда
2.1	Подводная лодка в надводном положении	несколько кв. метров.[6]
2.2	Рубка подводной лодки в надводном положении	несколько кв. метров. [6]
2.3	Катер	50
2.4	Ракетный катер	500
2.5	Эсминец	10000
2.6	Авианосец	50000[7]
3	Наземные цели
3.1	Автомобиль	3—10 (волна около 1 см)[8]
3.2	Танк Т-90 (длина волны 3—8 мм)	29[9][10]
4	Боеприпасы
4.1	Крылатая ракета ALCM (длина волны 8 мм)	<0.1
4.2	Головная часть оперативно-тактической ракеты	0,15—1,6[11]
4.3	Ядерная боеголовка БРПЛ(TN-75/TN-71)	0,01/0,1—0,25[12]
5	Прочие цели
5.1	Человек	0,8—1
6	Птицы[13] (со сложенными крыльями, длина волны 5 см)	(максимальная граница ЭПР)
6.1	Грач (Corvus frugilegus)	0,0048
6.2	Лебедь-шипун (Cygnus olor)	0,0228
6.3	Большой баклан (Phalacrocorax carbo)	0,0092
6.4	Красный коршун (Milvus Korshun)	0,0248
6.5	Кряква (Anas platyrhynchos)	0,0214
6.6	Серый гусь (Anser anser)	0,0225
6.7	Серая ворона (Corvus cornix)	0,0047
6.8	Полевой воробей (Passer montanus)	0,0008
6.9	Обыкновенный скворец (Sturnus vulgaris)	0,0023
6.10	Озёрная чайка (Larus ridibundus)	0,0052
6.11	Белый аист (Ciconia ciconia)	0,0287
6.12	Чибис (Vanellus vanellus)	0,0054
6.13	Гриф-индейка (Cathartes aura)	0,025
6.14	Сизый голубь (Columba livia)	0,01
6.15	Домовый воробей (Passer domesticus)	0,0008

ЭПР сосредоточенной цели

Двуточечная цель в разрешающем объёме локатора

Двуточечной целью будем называть пару целей, находящуюся в одном объёме разрешения РЛС. Используя формулу (4), можем найти амплитуды полей отражённой волны:

${\displaystyle \sigma =4\pi R^{2}{\frac {E_{2}^{2}}{E_{1}^{2}}}}$

${\displaystyle {\dot {U}}_{1}=U_{1}\exp(j\omega _{0}(t-t_{R_{1}}))}$	(19)
${\displaystyle {\dot {U}}_{2}=U_{2}\exp(j\omega _{0}(t-t_{R_{2}}))}$	(20)

Временные задержки можно рассчитать:

${\displaystyle t_{R_{1}}={\frac {2R_{1}}{c}}}$

${\displaystyle t_{R_{2}}={\frac {2R_{2}}{c}}}$

Отсюда:

${\displaystyle {\dot {U}}_{1}=U_{1}\exp(-j\omega _{0}t_{R_{1}}))=U_{1}\exp(-j\underbrace {2{\tfrac {2\pi }{\lambda }}R_{1}} _{\varphi _{1}})}$	(21)
${\displaystyle {\dot {U}}_{2}=U_{2}\exp(-j\omega _{0}t_{R_{2}}))=U_{2}\exp(-j\underbrace {2{\tfrac {2\pi }{\lambda }}R_{2}} _{\varphi _{2}})}$	(22)

К расчёту ЭПР двуточечной цели

тогда:

${\displaystyle U_{\Sigma }={\dot {U}}_{1}+{\dot {U}}_{2}=U_{1}e^{-j\varphi _{1}}+U_{2}e^{-j\varphi _{2}}}$

(23)

${\displaystyle U_{\Sigma }=\left|{\dot {U}}_{\Sigma }\right|={\sqrt {{\dot {U}}_{\Sigma }{\dot {U}}_{\Sigma }^{*}}}}$

${\displaystyle U_{\Sigma }={\sqrt {U_{1}^{2}+U_{2}^{2}-2U_{1}U_{2}\cos \varphi _{12}}}}$	(24)
${\displaystyle \phi _{12}=2kl\sin \gamma }$	(25)
${\displaystyle {\dot {U}}_{prm}=k_{1}{\sqrt {\sigma }}}$

Следовательно,

${\displaystyle \sigma _{\Sigma }=\sigma _{1}+\sigma _{2}+2{\sqrt {\sigma _{1}\sigma _{2}}}\cos(2{\tfrac {2\pi }{\lambda }}l\sin \gamma )}$

(26)

Диаграмма обратного рассеяния

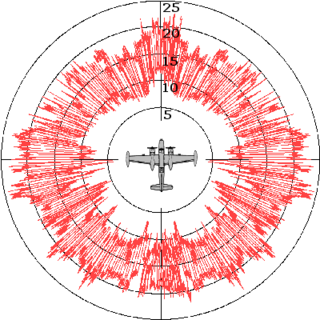
Зависимость ЭПР от угла отражения ${\displaystyle \sigma (\gamma )}$ — называется диаграммой обратного рассеяния (ДОР). ДОР будет иметь изрезанный характер и явно многолепестковый. При этом нули ДОР будут соответствовать противофазному сложению сигналов от цели в точке расположения РЛС, а ток — синфазному значению. При этом ЭПР может быть как больше, так и меньше ЭПР каждой из отдельных целей. Если волны приходят в противофазе, то будет наблюдаться минимум, а если в фазе, то максимум:

${\displaystyle \sigma _{min}=({\sqrt {\sigma _{1}}}-{\sqrt {\sigma _{2}}})^{2}}$

${\displaystyle \sigma _{max}=({\sqrt {\sigma _{1}}}+{\sqrt {\sigma _{2}}})^{2}}$

Пусть ${\displaystyle \sigma _{1}=\sigma _{2}=\sigma _{0}}$, тогда:

${\displaystyle \sigma =2\sigma _{0}(1+\cos(2{\tfrac {2\pi }{\lambda }}l\sin \gamma ))=4\sigma _{0}\cos ^{2}({\tfrac {2\pi }{\lambda }}l\sin \gamma )}$

Реальные объекты имеют несколько колеблющихся точек.

${\displaystyle {\dot {U}}_{\Sigma }=\sum _{i=1}^{N}{\dot {U}}_{i}=\sum _{i=1}^{N}U_{i}e^{-j\varphi _{i}}}$

${\displaystyle U_{\Sigma }=\left|{\dot {U}}_{\Sigma }\right|={\sqrt {\sum _{i=1}^{N}U_{i}e^{-j\varphi _{i}}\cdot \sum _{i=1}^{N}U_{i}e^{j\varphi _{i}}}}}$

${\displaystyle U_{\Sigma }=\sum _{i=1}^{N}U_{i}+2\sum _{i=1}^{N}\sum _{k=1}^{N}U_{i}U_{k}\cos \varphi _{i,k}}$

${\displaystyle \varphi _{i,k}\approx -\pi ..\pi }$, а значит ${\displaystyle \cos \varphi _{i,k}\approx 0}$.

Тогда суммарное поле:

${\displaystyle U_{\Sigma }=\sum _{i=1}^{N}U_{cp_{i}}^{2}\Rightarrow \sigma =\sum _{i=1}^{N}\sigma _{cp_{i}}}$

${\displaystyle \varphi _{i,k}}$ — определяется как изменение фазовых структур отражённой волны.

Фазовый фронт отражённой волны отличается от сферического.

Определение ЭПР распределённых целей

Распределённая цель — цель, размеры которой выходят за пределы разрешающего объёма РЛС.

Условие распределённости цели

Нарушение любого из условий вводит цель в класс распределённых

${\displaystyle {\begin{cases}l\leqslant \delta R\\l\leqslant \delta l_{h}\\l\leqslant \delta l_{w}\\\end{cases}}}$

Здесь:

• ${\displaystyle \delta R}$ — Размер разрешающего объёма РЛС по дальности;
• ${\displaystyle \delta l_{h}}$ — Размер разрешающего объёма РЛС по ширине (углу азимута);
• ${\displaystyle \delta l_{w}}$ — Размер разрешающего объёма РЛС по высоте (углу места);

То есть линейные размеры цели должны полностью находиться внутри элемента разрешения РЛС.

Если это не так, то в этом случае ЭПР цели будет суммой ЭПР каждого элементарного участка цели:

${\displaystyle \sigma =\sum _{i=1}^{N}\sigma _{cp_{i}}}$.

Если распределённый объект состоит из изотропных однотипных отражателей с одинаковыми свойствами, то общее ЭПР можно найти как произведение ЭПР на число отражателей:

${\displaystyle \sigma =N\cdot \sigma _{cp}}$

Число элементов такой цели обычно неизвестно.

Удельная ЭПР

В этом случае целесообразно ввести удельную ЭПР (σ_уд) — это ЭПР единичной площади (dS), или единичного объёма (dV) распределённой цели.

${\displaystyle \sigma _{S}=\sigma _{dS}\cdot S}$	(27)
${\displaystyle \sigma _{V}=\sigma _{dV}\cdot V}$	(28)

Здесь:

• ${\displaystyle \sigma _{dS}}$ — удельная ЭПР единичной поверхности ${\displaystyle [-]}$;
• ${\displaystyle \sigma _{dV}}$ — удельная ЭПР единичного объёма ${\displaystyle \left[{\tfrac {1}{m}}\right]}$;
• S — одновременно отражающая поверхность
• V — одновременно отражающий объём.

S и V целиком определяются размерами ширины диаграммы направленности и элементом разрешения по дальности, то есть параметрами излучённого сигнала.

Инфраструктура

Замер эффективной площади рассеяния габаритного макета летательного аппарата осуществляется следующим образом:

• 
  станция измерительного комплекса
• 
  высотный самолёт-разведчик A-12
• 
  ОТР «Сержант»
• 
  КРМБ «Томагавк»
• 
  Командный/служебный отсек КА «Аполлон»

См. также

• Технологии снижения заметности (Стелс)

Литература

• Смирнов А. Радиолокационная заметность объектов (рус.) // Армейский сборник : журнал. — 2013. — Ноябрь (т. 234, № 11). — С. 21—23.

Примечания

1. Финкельштейн М. И. Основы радиолокации. Учеб. для вузов. 2-е изд. / М.: Радио и связь, 1983. С. 126.
2. Skolnik M.I. Radar Handbook. 2nd ed. McGraw-Hill Professional, 1990.
3. Радиоэлектронные системы. Основы теории и построение. Справочник / Под ред. Я. Д. Ширмана / М.: ЗАО "Маквис", 1998. С. 127.
4. ФУНДАМЕНТАЛЬНЫЕ И ПРИКЛАДНЫЕ ПРОБЛЕМЫ СТЕЛС-ТЕХНОЛОГИЙ  (неопр.). Дата обращения: 18 мая 2014. Архивировано 23 октября 2014 года.
5. MASTER OF DEFENCE STUDIES RESEARCH PROJECT PASSIVE MULTISTATIC RADARS IN ANTI-STEALTH AIR DEFENCE
6. ЭПР не может быть равен нулю, но в данном случае он ничтожно мал.
7. Система управления вооружением СУВ-ВЭП «Меч» для истребителей серии Су-27, Су-30  (неопр.). Дата обращения: 18 ноября 2011. Архивировано 21 мая 2015 года.
8. «Визир» следует запретить! — 19 Марта 2009 — ПРИКОЛЫ НА ДОРОГАХ  (неопр.). Дата обращения: 24 декабря 2010. Архивировано 13 сентября 2009 года.
9. Маскировка — Комплекс поглощающих материалов и покрытий (недоступная ссылка)
10. Сотников А. М., Сидоренко Р. Г., Рыбалка Г. В. Оценка отражающих свойств наземных и воздушных объектов с пассивной защитой на основе композитных радиоизотопных покрытий  (рус.) (pdf). Харьковский университет Воздушных Сил им. И. Кожедуба, Харьков (15 января 2009). — Получены численные оценки отражающих свойств наземных и воздушных объектов с композитными радиоизотопными покрытиями. Проведенные численные исследования показывают принципиальную возможность и целесообразность применения композитных радиозотопных покрытий для защиты вооружения и военной техники от радиолокационных систем самонаведения сантиметрового и миллиметрового диапазона волн. Расчеты выполнены для однослойной и двухслойной структуры построения композитных радиозотопных покрытий. Дата обращения: 18 мая 2009. Архивировано 27 февраля 2012 года.
11. Казаков Е. Л, Казаков А. Е. Анализ целесообразности использования ложных целей для прорыва противоракетной обороны противника  (рус.) (pdf). Харьковский университет Воздушных Сил им. И. Кожедуба, Харьков (22 декабря 2008). Дата обращения: 18 мая 2009. Архивировано из оригинала 30 июля 2017 года.
12. Ядерный арсенал Франции  (неопр.). Дата обращения: 26 сентября 2012. Архивировано 30 ноября 2011 года.
13. Мацюра А. В. Использование различных типов радаров в орнитологических исследованиях  (рус.) (pdf). Мелитопольский государственный педагогический университет (25.04.05). Дата обращения: 23 августа 2009. Архивировано 27 февраля 2012 года.

Ссылки

• Что такое ЭПР — заметка в блоге dxdt.ru ^{[неавторитетный источник]}