Ряд Меркатора

Ряд Мерка́тора (иногда называемый ряд Ньютона — Меркатора) в математическом анализе — ряд Тейлора для функции натурального логарифма, впервые опубликованный немецким математиком Николасом Меркатором (Кауфманом) в трактате «Logarithmotechnia» (1668):

${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\cdots =\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}}$

Сходимость ряда Меркатора к ${\displaystyle \ln(1+x)}$ (показанной оранжевым) в окрестности нуля для 4, 7, 11, 16 членов ряда

Лейбниц за это открытие назвал Меркатора «первым изобретателем бесконечных рядов»; до Меркатора европейские математики рассматривали почти исключительно числовые ряды, не содержащие переменных. Независимо от Меркатора этот ряд открыл Исаак Ньютон. В работе «Метод флюксий и бесконечных рядов с приложением его к геометрии кривых» (1671, опубликован посмертно в 1736 году) Ньютон выразил удивление, что до Меркатора никто «не направил своего внимания на приложение к буквам [переменным] принципов недавно открытого учения о десятичных дробях, особенно потому, что при этом открывается путь к более трудным и более важным открытиям»^[1].

Ряд Меркатора способствовал подъёму массового интереса к использованию бесконечных рядов и формированию общей теории рядов и функций. К концу XVII века эта тема существенно расширилась и превратилась в математический анализ^[2].

Ряд Меркатора сходится при ${\displaystyle -1<x\leqslant 1,}$ хотя сходимость довольно медленная. При ${\displaystyle |x|<1}$ ряд сходится абсолютно.

История

Площадь под гиперболой ${\displaystyle y=1/x}$ в интервале ${\displaystyle (1,a)}$ равна ${\displaystyle \ln(a)}$

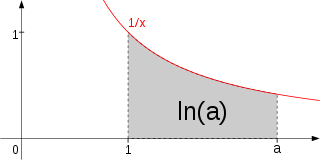
В 1647 году Грегуар де Сен-Венсан обнаружил связь логарифма и площади под гиперболой (см. рисунок). В 1650 году, исходя из геометрических соображений, итальянский математик Пьетро Менголи опубликовал в трактате «Новые арифметические квадратуры» разложение ${\displaystyle \ln 2}$ в бесконечный ряд^[3]:

${\displaystyle \ln 2={\frac {1}{1\cdot 2}}+{\frac {1}{3\cdot 4}}+{\frac {1}{5\cdot 6}}\dots }$

В 1657 году эту формулу независимо опубликовал английский математик Уильям Браункер в своей статье «Квадратура гиперболы с помощью бесконечного ряда рациональных чисел»^[3].

В 1668 году немецкий математик Николас Меркатор (Кауфман), проживавший тогда в Лондоне, в трактате «Logarithmotechnia» впервые рассмотрел разложение в ряд не числа, а функции^[4]:

${\displaystyle {\frac {1}{1+x}}=1-x+x^{2}-x^{3}+\dots }$

Далее он нашёл площади под левой и правой частями этого разложения (в современных терминах, проинтегрировал их) и получил «ряд Меркатора», который выписал для значений ${\displaystyle x=0{,}1}$ и ${\displaystyle x=0{,}21}$. Сходимость ряда Меркатор не исследовал, но сразу после выхода в свет труда Меркатора Джон Валлис указал, что ряд пригоден при ${\displaystyle 0\leqslant x<1}$ (отрицательными числами тогда пренебрегали).

Как обнаружили историки науки, Ньютон вывел такой же ряд в 1665 году, но, по своему обыкновению, не позаботился о публикации^[5]. Глубокие исследования Ньютона в области бесконечных рядов были опубликованы только в 1711 году, в трактате «Анализ с помощью уравнений с бесконечным числом членов»^[1].

Вариации и обобщения

Ряд Меркатора непригоден для реальных расчётов, так как сходится очень медленно, причём в ограниченном интервале. Но уже в год публикации Меркатора (1668) Джеймс Грегори предложил модифицированный его вариант:

${\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)}$

Этот ряд сходится гораздо быстрее, а логарифмируемое выражение уже может представить любое положительное число ${\displaystyle z={\frac {1+x}{1-x}}}$, ибо тогда ${\displaystyle x={\frac {z-1}{z+1}}}$ по абсолютной величине меньше единицы^[5]. Например, сумма первых 10 членов ряда Меркатора для ${\displaystyle \ln 2}$ равна ${\displaystyle 0{,}646,}$ здесь только первый десятичный знак верен, в то время как ряд Грегори даёт значение ${\displaystyle 0{,}6931471805498,}$ в котором верны 10 знаков из 13^[6].

На комплексной плоскости ряд Меркатора приобретает обобщённый вид:

${\displaystyle \sum _{n=1}^{\infty }{\frac {z^{n}}{n}}=z+{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}+{\frac {z^{4}}{4}}+\cdots }$

Это ряд Тейлора для комплексной функции ${\displaystyle f(z)=-\ln(1-z),}$ где символ ln обозначает главную ветвь (главное значение) комплексного натурального логарифма. Данный ряд сходится в круге ${\displaystyle |z|\leqslant 1,z\neq 1}$.

Примечания

1. Ньютон И. Математические работы. — М.—Л.: ОНТИ, 1937. — С. 3—24, 25. — 452 с.
2. Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича. — М.: Просвещение, 1977. — С. 121. — 224 с.
3. История математики, том II, 1970, с. 158.
4. История математики, том II, 1970, с. 158—161.
5. История математики, том II, 1970, с. 162.
6. Хайрер Э., Ваннер Г. Математический анализ в свете его истории. — М.: Научный мир, 2008. — С. 27. — 396 с. — ISBN 978-5-89176-485-9.

Литература

• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.

Ссылки

• Абельсон И. Б. Меркатор находит ключ // Рождение логарифмов. — М.—Л.: Гостехиздат, 1948. — 231 с.
• Weisstein, Eric W. Mercator Series (англ.) на сайте Wolfram MathWorld.