Равнобедренный треугольник

Равнобедренный треугольник — треугольник, в котором две стороны имеют равную длину. Боковыми называются равные стороны, а третья сторона — основанием. Каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно^[1].

Равнобедренный треугольник

Терминология

Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании^[1].

Евклид определил равнобедренный треугольник как треугольник, который имеет две равные стороны, но современная трактовка^[2] предпочитает определение, где треугольник имеет хотя бы две равные стороны, определяя таким образом равносторонний треугольник как частный случай равнобедренного.

Симметрия

Треугольник с двумя равными сторонами имеет одну ось симметрии, которая проходит через вершинный угол и середину основания. Эта ось симметрии совпадает с биссектрисой вершинного угла, медианой, проведённой к основанию, высотой, проведённой из вершинного угла и с серединным перпендикуляром^{[3][уточнить]}.

Свойства

Основной источник: ^[1]

Свойства равнобедренного треугольника

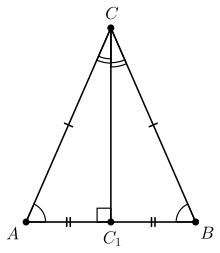
В равнобедренном треугольнике углы при основании равны. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.

Пусть a — длина равных боковых сторон, b — длина основания, h — высота к основанию, R — радиус описанной окружности

• ${\displaystyle a={\frac {b}{2\cos \alpha }}}$ (следствие теоремы косинусов);
• ${\displaystyle a^{2}=2Rh}$;
• ${\displaystyle b=a{\sqrt {2(1-\cos \beta )}}}$ (следствие теоремы косинусов);
• ${\displaystyle b=2a\sin {\frac {\beta }{2}}}$;
• ${\displaystyle b=2a\cos \alpha }$ (теорема о проекциях);

Радиус вписанной окружности может быть выражен пятью способами в зависимости от того, какие два параметра равнобедренного треугольника известны:

• ${\displaystyle r={\frac {b}{2}}{\sqrt {\frac {2a-b}{2a+b}}}}$
• ${\displaystyle r={\frac {bh}{b+{\sqrt {4h^{2}+b^{2}}}}}}$
• ${\displaystyle r={\frac {h}{1+{\frac {a}{\sqrt {a^{2}-h^{2}}}}}}}$
• ${\displaystyle r={\frac {b}{2}}\operatorname {tg} \left({\frac {\alpha }{2}}\right)}$
• ${\displaystyle r=a\cdot \cos(\alpha )\cdot \operatorname {tg} \left({\frac {\alpha }{2}}\right)}$

Углы могут быть выражены следующими способами:

• ${\displaystyle \alpha ={\frac {\pi -\beta }{2}};}$
• ${\displaystyle \beta =\pi -2\alpha$ ;}
• ${\displaystyle \alpha =\arcsin {\frac {a}{2R}},\beta =\arcsin {\frac {b}{2R}}}$ (теорема синусов).
• Угол также может быть найден без ${\displaystyle {\pi }}$ и ${\displaystyle R}$. Треугольник делится медианой пополам, и в полученных двух равных прямоугольных треугольниках вычисляются углы :

${\displaystyle y=\cos \alpha ={\frac {b}{c}},\arccos y=x}$

Периметр равнобедренного треугольника находится следующими способами:

• ${\displaystyle P=2a+b}$ (по определению);
• ${\displaystyle P=2R(2\sin \alpha +\sin \beta )}$ (следствие теоремы синусов).

Площадь треугольника находится следующими способами:

${\displaystyle S={\frac {1}{2}}bh;}$

${\displaystyle S={\frac {1}{2}}a^{2}\sin \beta ={\frac {1}{2}}ab\sin \alpha ={\frac {b^{2}}{4\tan {\frac {\beta }{2}}}};}$

${\displaystyle S={\frac {1}{2}}b{\sqrt {\left(a+{\frac {1}{2}}b\right)\left(a-{\frac {1}{2}}b\right)}};}$

Теорема Лемуса-Штейнера

Основной источник: ^[4]

Если две биссектрисы треугольника равны, то этот треугольник — равнобедренный.

Лемус, Штейнер, XIX в.

Доказан этот признак равнобедренного треугольника был только в XIX веке двумя математиками, Лемусом и Штейнером, которые обменивались письмами в течение нескольких лет.

См. также

• Теорема о равнобедренном треугольнике
• Равнобедренный прямоугольный треугольник