Годичный звёздный параллакс

Годи́чный паралла́кс звезды́ — изменение координат звезды, вызванное изменением положения наблюдателя из-за орбитального движения Земли вокруг Солнца.

Параллактические эллипсы звёзд при различных расстояниях от плоскости эклиптики

Является доказательством движения Земли вокруг Солнца и основным методом измерения расстояний до звёзд.

Величина годичного параллакса данной звезды равна углу, под которым большая полуось земной орбиты видна с расстояния этой звезды. Ввиду очень больших расстояний до звёзд годичные параллаксы даже у ближайших из них не превосходят одной секунды дуги.

Основные положения

Годичный параллакс у звёзд вблизи плоскости эклиптики (слева) и полюса эклиптики (справа).

Из-за обращения Земли вокруг Солнца положения звёзд на небесной сфере испытывают параллактическое смещение. Видимая форма траектории звезды на небесной сфере имеет форму эллипса, большая полуось которого параллельна эклиптике.

Если звезда наблюдается вблизи эклиптики, то максимальный параллактический угол, то есть угол, образованный звездой, Землёй и Солнцем, находится из геометрического соотношения:

${\displaystyle \sin p={\frac {a}{r}},}$

где ${\displaystyle a}$ — расстояние между Землёй и Солнцем,

${\displaystyle r}$ — расстояние от Солнца до звезды.

Если звезда наблюдается вблизи полюса эклиптики, то параллактический угол вычисляется по формуле

${\displaystyle \operatorname {tg} p={\frac {a}{r}}.}$

Поскольку годичные параллаксы звёзд чрезвычайно малы, синус и тангенс угла ${\displaystyle p}$ с очень высокой точностью равны значению самого этого угла, выраженного в радианах. Поэтому, в любом случае положения звезды, параллакс прямо пропорционален расстоянию от Земли до Солнца (одна астрономическая единица) и обратно пропорционален расстоянию до звезды. Из измеренного значения годичного параллакса звезды ${\displaystyle p,}$ выраженный в угловых секундах, можно рассчитать расстояние ${\displaystyle r}$ до неё, выраженное в парсеках (пк), по следующей формуле^[1]:

${\displaystyle r={\frac {1}{p}}.}$

Например, звезда, с годовым параллаксом в 1", находится на расстоянии 1 пк; звезда, имеющая параллакс 0,1", находится на расстоянии 10 пк; и так далее. Для далёких звёзд параллакс мал и его часто выражают в миллиарксекундах (mas) и микроарксекундах (μas). Соответственно, расстояние до звезды с параллаксом 1 mas составляет 1000 пк (1 кпк), а с параллаксом 1 μas — 1 000 000 пк (1 Мпк).

Параллактическое смещение близких звёзд на фоне далёких звёзд.

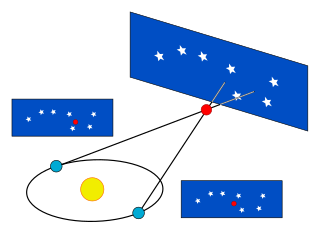
Практически при измерении звёздных параллаксов обычно определяют годовое перемещение звезды относительно других, существенно более слабых звёзд, которые предполагаются гораздо более удалёнными, чем исследуемая звезда (так называемый дифференциальный метод измерения годичных параллаксов).

Если параллакс звезды определён непосредственным измерением параллактических углов, и, соответственно, расстояния до звезды, как описано выше, то говорят о тригонометрическом параллаксе^[2].

Помимо тригонометрического определения расстояния развиты и другие методы определения расстояний до звёзд. Например, изучение спектров некоторых звёзд позволяет оценить их абсолютную звёздную величину и по измерениям видимой звёздной величины — расстояние до звезды. Если рассчитанное таким способом расстояние пересчитать в параллактический угол, то эту величину называют спектральным параллаксом^[2].

Существуют также динамический, групповой, средний и энергетический параллаксы^[1], но все методы определения расстояний требуют калибровки с помощью тригонометрического метода. Также при оценке измеренного параллакса необходима коррекция с учётом эффекта Лутца — Келкера.

История

Памятник Аристарху Самосскому в Аристотелевском университете, Салоники

История поисков звёздных параллаксов неразрывно связана с проблемой движения Земли, утверждением гелиоцентрической системы мира.

Гелиоцентрическая система мира впервые была предложена древнегреческим астрономом Аристархом Самосским (III век до н. э.). Архимед (один из основных источников наших знаний об этой теории) сообщает, что по мнению Аристарха размер сферы неподвижных звёзд «таков, что окружность, описываемая, по его предположению, Землёй, находится к расстоянию неподвижных звёзд в таком же отношении, в каком центр шара находится к его поверхности»^[3]. Вероятно, это означает, что Аристарх объяснил ненаблюдаемость годичных параллаксов звёзд их огромной удалённостью — настолько большой, что радиус земной орбиты пренебрежимо мал по сравнению с расстоянием до звёзд^[4][5][6].

Николай Коперник

Когда гелиоцентрическая системе мира была заново предложена в начале XVI века польским астрономом Николаем Коперником, вопрос о ненаблюдаемости годичных параллаксов встал вновь. Коперник объяснил это как и Аристарх за 1800 лет до него^[7]: звёзды слишком далеки, чтобы их годичные параллаксы были доступны непосредственным измерениям. Как он пишет в своей книге «О вращении небесных сфер», отсутствие годичных параллаксов у звёзд

…только доказывает неизмеримую их высоту, которая заставляет исчезать из вида даже орбиту годового движения или её отображение, так как всякому видимому предмету соответствует некоторая величина расстояния, за которой он больше уже не замечается, как показано в оптике^[8]

Ответ Коперника не убеждал сторонников геоцентрической системы мира и неподвижности Земли. Попытки измерения годичных параллаксов были предприняты датским астрономом Тихо Браге в конце XVI века; но ни у одной из 777 звёзд, входящих в его каталог, он не обнаружил параллакс^[9]. Bзамен системе мира Коперника он предложил свою собственную систему - гео-гелиоцентрическую систему мира. Браге утверждал, что если звёзды настолько далеки, как предполагают коперниканцы, то, во-первых, расстояние от Сатурна до звёзд должно быть непропорционально большим, и во-вторых, звёзды в этом случае должны иметь непропорционально большой линейный размер. Эти же доводы против гелиоцентрической системы неоднократно повторялись и астрономами следующего, XVII века; так, они были перечислены в числе 77 доводов против Коперника в «Новом Альмагесте» известного итальянского астронома Джованни Баттиста Риччиоли.

Галилео Галилей

Сторонники гелиоцентрической системы безуспешно искали годичные параллаксы на протяжении всего XVII века. Предполагается, что в 1617 году поиск годичного параллакса у звезды Мицар в Большой Медведице был произведён Галилео Галилеем и Бенедетто Кастелли в Италии^[10][11][12]. Именно Галилей в 1611 году предложил дифференциальный метод определения параллаксов: если все звёзды удалены на разные расстояния от Земли, то более близкие звёзды будут смещаться сильнее, чем более далёкие звёзды, но расположенные на небесной сфере рядом (независимо от Галилея этот метод был предложен также итальянцем Лодовико Рампони^[13]). Галилей описал этот метод в своих знаменитых «Диалогах о двух главнейших системах мира»^[14][15].

В 1666 году английский физик и астроном Роберт Гук заявил, что ему, наконец, удалось обнаружить годичный параллакс у звезды γ Дракона. Подробное описание своих наблюдений Гук изложил в трактате «Попытка доказательства движения Земли»^[16] (1674 год), однако его заявления были восприняты с большим скептицизмом^[17].

В период с 1674 по в 1681 год Жан Пикар во Франции предпринял несколько попыток обнаружить параллакс яркой звезды в созвездии Лиры, однако все они закончились неудачей.

В 1689 году с заявлением об обнаружении параллакса Полярной звезды выступил английский астроном Джон Флемстид, однако его работа была раскритикована Жаком Кассини^{[18][K 1]}.

Возможность обнаружение годичных параллаксов находилось далеко за пределами возможностей инструментов астрономов этого времени.

В XVIII и начале XIX века работа по обнаружению годичных параллаксов по-прежнему не давала результаты. В то время астрономы уже не сомневались в истинности гелиоцентрической системе, и обнаружение параллаксов по-прежнему был актуально, поскольку это был единственный, известный в то время, метод измерения расстояний до звёзд.

В ходе поисков годичных параллаксов были сделаны другие важные открытия: аберрация света и нутация земной оси (Джеймс Брэдли, 1727—1728 годы)^[19], орбитальное движение компонент двойных звёзд (Уильям Гершель, 1803—1804 годы)^[20]. Однако у астрономов ещё не было достаточно точных инструментов для обнаружения параллакса.

• Авторы первых успешных измерений годичных параллаксов звёзд
• 
  Фридрих Георг Вильгельм (Василий Яковлевич) Струве
• 
  Фридрих Вильгельм Бессель
• 
  Томас Джеймс Хендерсон

В 1814 году к работе по обнаружению годичных параллаксов приступил Фридрих Вильгельм Струве в Дерптской обсерватории. Первые измерения, выполненные им до 1821 года, имели большие инструментальные ошибки и не удовлетворили Струве, но, по крайне мере, ему удалось указать правильные числовые порядки параллаксов нескольких ярких звёзд^[21]. Так, полученный им параллакс Альтаира (0,181±0,094") достаточно близок к современному значению (0,195")^[22].

В 1837 году Струве (с помощью Фраунгоферовского рефрактора, установленного в Дерптской обсерватории) удалось измерить параллакс Веги (α Лиры), оказавшийся равным 0,125±0,055". Этот результат был опубликован Струве в книге «Микрометрические измерения двойных звёзд», где также были приведены критерии, по которым нужно отбирать звёзды для поиска их параллаксов, и заложены основы метода динамических параллаксов. Однако сам Струве считал полученное им значение параллакса Веги предварительным. Новые измерения Струве, опубликованные в 1839 году, привели к вдвое большему результату, 0,262±0,025", что заставляло учёных сомневаться в надёжности его измерений. Как показал в 1952 году пулковский астроном А. Н. Дейч, измерения Струве были достаточно точными, но он ошибся при обработке данных: при правильной обработке своих данных Струве получил бы достаточно точное значение параллакса звезды. В настоящее время измеренный параллакс Веги равен 0,128", что практически совпадает с первым измерением Струве.

Фраунгоферовский гелиометр Кёнигсбергской обсерватории, с помощью которого Бессель обнаружил годичный параллакс 61 Лебедя

В том же 1838 году немецкому астроному и математику Фридриху Бесселю в Кёнигсбергской обсерватории удалось измерить параллакс звезды 61 Лебедя, оказавшийся равным 0,314±0,014" (современное значение 0,287"). При этом был использован гелиометр, который, как и Дерптский рефрактор Струве, был изготовлен Й. Фраунгофером. Бесселю удалось наблюдать периодическое изменение углового расстояния 61 Лебедя от двух рядом расположенных на небесной сфере слабых звёзд сравнения и установить, за год звезда описывает на небесной сфере маленький эллипс, как и предсказывает теория. Именно поэтому приоритет в открытии годичных параллаксов у звёзд обычно приписывают Бесселю.

Наконец, в 1838 году были обнародованы также данные английского астронома Томаса Хендерсона (обсерватория Мыса Доброй Надежды), которому удалось измерить параллакс звезды α Центавра: 1,16±0,11" (современное значение 0,747"). Имея в виду работы Бесселя, Струве и Хендерсона, выдающийся английский астроном Джон Гершель сказал: «стена, мешавшая нашему проникновению в звёздную вселенную, почти одновременно была пробита в трёх местах»^[23].

Прогресс в определении годичных параллаксов тормозился значительными систематическими ошибками инструментов и конкретных наблюдателей. К концу XIX века были определены параллаксы не более сотни звёзд, причём результаты измерений для каждой конкретной звезды сильно различались в разнгых обсерваториях^[24].

Ситуация в значительной мере была исправлена применением фотографии с конца XIX века. Стандартный метод фотографического определения параллаксов был разработан американским астрономом Фрэнком Шлезингером в 1903 году. Благодаря работам Шлезингера инструментальные ошибки при определении параллаксов были снижены до 0,01". Каталог параллаксов Шлезингера, опубликованный в 1924 году, содержал 1870 надёжно измеренных параллаксов^[25].

Современное состояние вопроса

Область Млечного пути, доступная для измерения параллаксов, была увеличена в 10 раз благодаря запуску космического телескопа «Хаббл»

Макет космического аппарата Gaia на салоне Ле Бурже, 2013

В настоящее время (2025 год) наземные оптические наблюдения позволяют в некоторых случаях снизить ошибку в измерении параллакса до 0,005"^[26], что соответствует предельному расстоянию, измеренному с приемлемой ошибкой, в 200 пк. Дальнейшее повышение точности измерений стало возможным благодаря использованию космических телескопов. Специально для астрометрических целей Европейским космическим агентством (ЕКА) в 1989 году был запущен космический телескоп Hipparcos, позволивший измерить параллаксы более 100 тысяч звёзд с точностью до 0,001". В 2013 году ЕКА запустило новый космический телескоп — Gaia. Планируемая точность измерения параллакса звёзд ярче 15 m будет выше 25 миллионных долей секунды, а для слабых звёзд (около 20 m) — до 300 миллионных долей секунды.

Измерение годичных параллаксов позволяет производить также один из инструментов Космического телескопа им. Хаббла — Широкоугольная камера 3. Точность измерения параллаксов составляет от 20 до 40 миллионных долей секунды, что позволяет измерять с приемлемой ошибкой расстояния до 5 килопарсек. В частности, был измерен параллакс переменной звезды SU Возничего^[27][28].

Значительным достижением конца XX века явилось использование для параллактических измерений космических радиоисточников метода сверхдальной радиоинтерферометрии^[29]. Погрешность при этом может составлять до 10 миллионных долей угловой секунды. Этот метод применяется для измерения расстояния до компактных радиоисточников — космических мазеров, радиопульсаров и др. Так, с помощью этого метода удалось измерить расстояние до объекта Стрелец B2 — газопылевого облака с бурным звездообразованием, находящимся в 100—120 парсеках от центра нашей Галактики. Результаты измерений показали, что Стрелец B2 расположен на расстоянии 7,8±0,8 кпк, что даёт расстояние до центра Галактики 7,9±0,8 кпк^[30]. Измерение параллаксов ультракомпактных внегалактических радиоисточников является одной из целей планируемого российского космического эксперимента Миллиметрон — космической обсерватории миллиметрового, субмиллиметрового и инфракрасного диапазонов^[31].

См. также

• Шкала расстояний в астрономии
• Стандартная линейка
• Собственное движение

Комментарии

1. Возможно, Гуку и Флемстиду действительно удалось зарегистрировать смещение звёзд, но вызванное не годичным параллаксом, а аберрацией света, которая, как впоследствии показал Брэдли, также является доказательством вращения Земли вокруг Солнца (Fernie 1975, p. 223).