operație la nivel de biți în informatică From Wikipedia, the free encyclopedia
În matematica combinatorică o deplasare circulară este operația de rearanjare a intrărilor într-un tuplu(d), fie prin mutarea intrării finale în prima poziție, în timp ce deplasarea tuturor celorlalte intrări în următoarea poziție, fie prin efectuarea operației inverse. O deplasare circulară este un tip particular de permutare ciclică, care la rândul său este un tip particular de permutare. Formal, o deplasare circulară este o permutare σ a celor n intrări din tuplu, astfel încât fie
sau
Rezultatele aplicării repetate a operației de deplasare circulară asupra unui tuplu dat sunt numite deplasări circulare ale tuplului.
De exemplu, aplicarea repetată a deplasărilor circulare la 4-tuplul (a, b, c, d) dă succesiv
și apoi secvența se repetă; acest 4-tuplu are, prin urmare, patru deplasări circulare distincte. Totuși, nu toate n-tuplurile au n deplasări circulare distincte. De exemplu, 4-tuplul (a, b, a, b) are doar 2 deplasări circulare distincte. În general, numărul de deplasări circulare ale unui n-tuplu poate fi orice divizor al lui n, în funcție de intrările tuplului.
În programare, o rotație pe biți (deplasare circulară), este o operație pe biți care deplasează toți biții operandului său. Spre deosebire de o deplasare aritmetică, o deplasare circulară nu păstrează bitul semn al unui număr și nu distinge exponentul unui număr în virgulă mobilă de mantisă. Spre deosebire de o deplasare logică, pozițiile de biți libere nu sunt completate cu zerouri, ci sunt completate cu biții care sunt mutați în afara șirului.
Deplasările circulare sunt folosite adesea în criptografie pentru a permuta șirurile de biți. Din păcate, multe limbaje de programare, inclusiv C, nu au operatori sau funcții standard pentru deplasarea circulară, chiar dacă practic toate procesoarele au instrucțiuni pentru operații pe biți(d) pentru aceasta (de exemplu, Intel x86 are ROL și ROR). Totuși, unele compilatoare pot oferi acces la instrucțiunile procesorului prin intermediul funcțiilor intrinseci. În plus, unele construcții din codul standard ANSI C pot fi optimizate de către un compilator pentru a folosi instrucțiunile din limbajul de asamblare „rotire” pe procesoarele care au o astfel de instrucțiune. Majoritatea compilatoarelor C recunosc următorul idiom și îl compilează într-o singură instrucțiune de rotație pe 32 de biți.[1][2]
/*
* Operațiile de deplasare în C sunt definite numai pentru valorile deplasate
* care nu sunt negative și mai mici decât sizeof(value) * CHAR_BIT.
* Masca, folosită pe biți și (&), previne comportamentul nedefinit
* când numărul de deplasări este 0 sau >= lungimea unui întreg fără semn.
*/
#include <stdint.h> // pentru uint32_t, pentru a avea rotații pe 32 de biți, indiferent de dimensiunea întregului.
#include <limits.h> // pentru CHAR_BIT
uint32_t rotl32 (uint32_t value, unsigned int count) {
const unsigned int mask = CHAR_BIT * sizeof(value) - 1;
count &= mask;
return (value << count) | (value >> (-count & mask));
}
uint32_t rotr32 (uint32_t value, unsigned int count) {
const unsigned int mask = CHAR_BIT * sizeof(value) - 1;
count &= mask;
return (value >> count) | (value << (-count & mask));
}
Această implementare sigură și ușor de compilat a fost dezvoltată de John Regehr,[3] și publicată ulterior de Peter Cordes.[4][5]
Atunci când număr este limitat la intervalul de la 1 la 31 de biți, adesea este folosită o versiune mai simplă:
uint32_t rotl32 (uint32_t value, unsigned int count) {
return value << count | value >> (32 - count);
}
Această versiune este periculoasă deoarece dacă număr este 0 sau 32, cere o deplasare de 32 de biți, care este un comportament nedefinit în standardul limbajului C. Totuși, oricum tinde să funcționeze, deoarece majoritatea microprocesoarelor implementează valoarea >> 32 fie ca o schimbare de 32 de biți (producând 0), fie o deplasare de 0 biți (producând valoarea inițială), și oricare dintre ele produce rezultatul corect în această aplicație.
Dacă șirul de biți 0001 0111 a fost supus unei deplasări circulare cu o poziție... (vezi imaginile de mai jos)
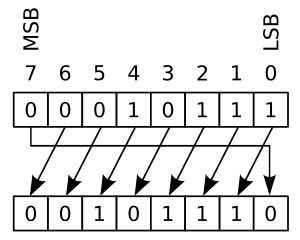 |
 |
Dacă șirul de biți 1001 0110 a fost supus următoarelor operații:
| deplasare circulară la stânga cu 1 poziție: | 0010 1101 |
| deplasare circulară la stânga cu 2 poziții: | 0101 1010 |
| deplasare circulară la stânga cu 3 poziții: | 1011 0100 |
| deplasare circulară la stânga cu 4 poziții: | 0110 1001 |
| deplasare circulară la stânga cu 5 poziții: | 1101 0010 |
| deplasare circulară la stânga cu 6 poziții: | 1010 0101 |
| deplasare circulară la stânga cu 7 poziții: | 0100 1011 |
| deplasare circulară la stânga cu 8 poziții: | 1001 0110 |
| deplasare circulară la dreapta cu 1 poziție: | 0100 1011 |
| deplasare circulară la dreapta cu 2 poziții: | 1010 0101 |
| deplasare circulară la dreapta cu 3 poziții: | 1101 0010 |
| deplasare circulară la dreapta cu 4 poziții: | 0110 1001 |
| deplasare circulară la dreapta cu 5 poziții: | 1011 0100 |
| deplasare circulară la dreapta cu 6 poziții: | 0101 1010 |
| deplasare circulară la dreapta cu 7 poziții: | 0010 1101 |
| deplasare circulară la dreapta cu 8 poziții: | 1001 0110 |
Codurile ciclice(d) sunt un tip de coduri bloc(d) cu proprietatea că deplasarea circulară a unui cuvânt de cod va produce întotdeauna un alt cuvânt de cod. Acest lucru motivează următoarea definiție generală: Pentru un șir(d) s peste un alfabet Σ, fie ca shift(s) să noteze setul de deplasări circulare ale s, iar pentru o mulțime de L de șiruri, fie ca shift(L) să noteze setul tuturor deplasărilor circulare ale șirurilor din L. Dacă L este un cod ciclic, atunci shift(L) ⊆ L; aceasta este o condiție necesară pentru ca L să fie un limbaj ciclic(d). Operația shift(L) a fost studiată în teoria limbajelor formale. De exemplu, dacă L este un limbaj independent de context, atunci shift(L) este și el independent de context.[6][7] De asemenea, dacă L este descris printr-o expresie regulată de lungimea n, există o expresie regulată cu lungimea O(n3) care descrie shift („L”).[8]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.