Fagure simplectic

În geometrie un fagure simplectic (sau fagure n-simplex) este o serie infinit dimensională de faguri, bazați pe simetria afină ${\displaystyle {\tilde {A}}_{n}}$ a grupului Coxeter. Are simbolul Schläfli {3^[n+1]} și este reprezentat printr-o diagramă Coxeter–Dynkin ca un graf ciclic cu n+1 noduri cu un nod inelat. Este format din fațete n-simplexuri, împreună cu toate n-simplexurile rectificate. Poate fi considerat ca un fagure hipercubic n-dimensional care a fost subdivizat de-a lungul tuturor hiperplanelor ${\displaystyle x+y+...\in \mathbb {Z} }$, apoi întins de-a lungul diagonalei sale principale până când simplexurile de la capetele hipercuburilor devin regulate. Figura vârfului unui fagure n-simplex este un n-simplex expandat.

${\displaystyle {\tilde {A}}_{2}}$	${\displaystyle {\tilde {A}}_{3}}$
Pavare triunghiulară	Fagure tetraedric-octaedric
Cu triunghiuri echilaterale roșii și galbene	Cu tetraedre turcoaz și galbene și tetraedre rectificate (octaedre) roșii

În spațiul bidimensional fagurele simplectic este pavarea triunghiulară, cu diagrama Coxeter umplând planul cu triunghiuri colorate alternativ. În spațiul tridimensional fagurele simplectic este fagurele tetraedric-octaedric, cu diagrama Coxeter umplând spațiul cu celule alternativ tetraedrice și octaedrice. În spațiul cvadridimensional este fagurele 5-celule, cu diagrama Coxeter , cu fațetele formate din 5-celule și 5-celule rectificat. În 5 dimensiuni este fagurele 5-simplex, cu diagrama Coxeter , umplând spațiul cu 5-simplexuri, 5-simplexuri rectificate și 5-simplexuri birectificate. În 6 dimensiuni este fagurele 6-simplex, cu diagrama Coxeter , umplând spațiul cu 6-simplexuri, 6-simplexuri rectificate și fațete 6-simplexuri birectificate.

După dimensiune

n	${\displaystyle {\tilde {A}}_{2+}}$	Teselare	Figura vârfului	Fațete pe figura vârfului	Vârfuri pe figura vârfului	Figura laturii
1	${\displaystyle {\tilde {A}}_{1}}$	Apeirogon		1	2	-
2	${\displaystyle {\tilde {A}}_{2}}$	Pavare triunghiulară fagure 2-simplex	Hexagon (Triunghi trunchiat)	3+3 triunghiuri	6	Segment
3	${\displaystyle {\tilde {A}}_{3}}$	Fagure tetraedric-octaedric fagure 3-simplex	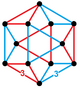Cuboctaedru (Tetraedru cantelat)	4+4 tetraedre 6 tetraedre rectificate	12	Dreptunghi
4	${\displaystyle {\tilde {A}}_{4}}$	Fagure 4-simplex	5-celule runcinat	5+5 5-celule 10+10 5-celule rectificat	20	Antiprismă triunghiulară
5	${\displaystyle {\tilde {A}}_{5}}$	Fagure 5-simplex	5-simplex stericat	6+6 5-simplex 15+15 5-simplex rectificat 20 5-simplex birectificat	30	Antiprismă tetraedrică
6	${\displaystyle {\tilde {A}}_{6}}$	Fagure 6-simplex	...	...	...	...

Proiecție prin „plieri”

Fagurii (2n−1)-simplex și fagurii 2n-simplex pot fi proiectați în fagurele hipercubic n-dimensional printr-o operație de pliere geometrică care aplică două perechi de oglinzi una pe cealaltă, având în comun același aranjament al vârfurilor:

${\displaystyle {\tilde {A}}_{2}}$		${\displaystyle {\tilde {A}}_{4}}$		${\displaystyle {\tilde {A}}_{6}}$		${\displaystyle {\tilde {A}}_{8}}$		${\displaystyle {\tilde {A}}_{10}}$		...
${\displaystyle {\tilde {A}}_{3}}$		${\displaystyle {\tilde {A}}_{3}}$		${\displaystyle {\tilde {A}}_{5}}$		${\displaystyle {\tilde {A}}_{7}}$		${\displaystyle {\tilde {A}}_{9}}$		...
${\displaystyle {\tilde {C}}_{1}}$		${\displaystyle {\tilde {C}}_{2}}$		${\displaystyle {\tilde {C}}_{3}}$		${\displaystyle {\tilde {C}}_{4}}$		${\displaystyle {\tilde {C}}_{5}}$		...

Bibliografie

• en George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
• en Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
• en Norman Johnson Uniform Polytopes, Manuscript (1991)
• en Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8
• en Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6

• (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
• (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

Vezi și

	Portal Matematică

• Fagure hipercubic

v • d • m Faguri convecși regulați și uniformi în dimensiunile 2–8
Spațiu	Familia	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Pavare uniformă	{3[3]}	δ3	hδ3	qδ3	Hexagonală
E3	Fagure convex uniform	{3[4]}	δ4	hδ4	qδ4
E4	4-fagure uniform	{3[5]}	δ5	hδ5	qδ5	Fagure 24-celule
E5	5-fagure uniform	{3[6]}	δ6	hδ6	qδ6
E6	6-fagure uniform	{3[7]}	δ7	hδ7	qδ7	222
E7	7-fagure uniform	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	8-fagure uniform	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
En-1	(n−1)-fagure uniform	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21