Distribuição logística

 Nota: Este artigo é sobre o conceito matemático. Para o conceito da logística, veja Distribuição (logística).

A distribuição logística deriva do trabalho de Pierre François Verhulst, professor de análise na Faculdade Militar Belga, que utilizou esta distribuição para modelar o crescimento da população na Bélgica no início de 1800 ^[1]. A teoria da probabilidade e a estatística são dois ramos da matemática onde a distribuição logística é classificada como sendo uma distribuição de probabilidade contínua. Um aspeto peculiar é que a distribuição de Tukey Lambda representa uma generalização da distribuição logística, uma vez que o parâmetro ${\displaystyle \lambda }$ desta distribuição, quando igualado a zero, corresponde à distribuição logística.

Notação

Seja ${\displaystyle X}$ uma variável aleatória contínua. Se ${\displaystyle X}$ segue uma distribuição logística com parâmetros ${\displaystyle \mu }$ e ${\displaystyle s}$, denota-se por ${\displaystyle X\sim L(\mu ,s)}$, onde ${\displaystyle \mu }$ representa o parâmetro de localização e ${\displaystyle s}$ o parâmetro de escala ^[2].

Quando ${\displaystyle \mu =0}$ e ${\displaystyle s=1}$, a distribuição logística é designada por distribuição logística padrão ou standard, ${\displaystyle X\sim L(0,1)}$.

Função densidade de probabilidade

Figura 1 — Gráfico da função densidade de probabilidade

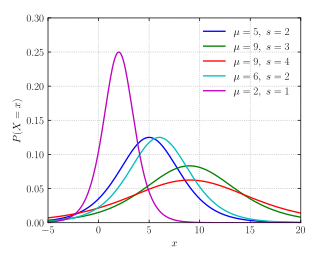
A função densidade de probabilidade, abreviada por f.d.p.. Para a variável aleatória ${\displaystyle X}$, é dada por:

${\displaystyle f(x;\mu ,s)={\dfrac {e^{-\left({\dfrac {x-\mu }{s}}\right)}}{s\left[1+e^{-\left({\dfrac {x-\mu }{s}}\right)}\right]^{2}}}}$, onde ${\displaystyle x,\mu \in R}$ e ${\displaystyle s>0}$ ^[2].

Os parâmetros de localização e de escala influenciam a representação gráfica da f.d.p. da distribuição logística. Na Figura 1, é possível observar que, para diferentes valores do parâmetro de localização, a função desloca-se ao longo do eixo das abcissas. O parâmetro de escala influencia a função em termos da sua altura. Consoante os diferentes valores de ${\displaystyle s}$, a função pode se tornar mais alta e achatada ou mais baixa e larga. Em geral, a f.d.p. é unimodal e possui apenas um único máximo global (na Figura 1, representa o "pico" da função).

A função secante hiperbólica, designada por ${\displaystyle sech}$, é dada por ${\displaystyle sech(x)={\dfrac {2}{e^{x}+e^{-x}}}}$. A f.d.p. pode ser escrita em termos do quadrado desta função. Assim, é possível reescrever a f.d.p. usando ${\displaystyle sech^{2}}$, de tal forma que se obtém a seguinte expressão:

${\displaystyle f(x;\mu ,s)={\dfrac {1}{s\left[e^{\dfrac {x-\mu }{2s}}+e^{-\left({\dfrac {x-\mu }{2s}}\right)}\right]^{2}}}={\dfrac {1}{4s}}sech^{2}\left({\dfrac {x-\mu }{2s}}\right)}$, onde ${\displaystyle x,\mu \in R}$ e ${\displaystyle s>0}$.

Função distribuição

Figura 2 — Gráfico da função distribuição

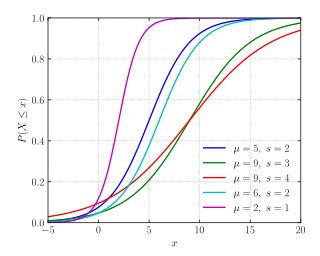
A função distribuição para a variável aleatória ${\displaystyle X}$ é dada por:${\displaystyle F(x;\mu ,s)={\dfrac {1}{1+e^{-\left({\dfrac {x-\mu }{s}}\right)}}}}$, onde ${\displaystyle x,\mu \in R}$ e ${\displaystyle s>0}$ ^[2].

A função logística é definida por ${\displaystyle f(x)={\dfrac {1}{1+e^{-x}}}}$. Verifica-se pela expressão da função distribuição que esta se assemelha à função logística. Deste modo, o gráfico da Figura 2 é muito semelhante ao gráfico da função logística. Pela Figura 2, observa-se que, para diferentes valores de ${\displaystyle \mu }$ e ${\displaystyle s}$, a curva exibe um crescimento exponencial mais ou menos acentuado.

A função tangente hiperbólica, designada por ${\displaystyle tanh}$, é dada por ${\displaystyle tanh(x)={\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$. A função distribuição pode ser escrita usando a função ${\displaystyle tanh}$. Assim, a expressão anterior da função distribuição é reescrita obtendo-se

${\displaystyle F(x;\mu ,s)={\dfrac {1}{2}}+{\dfrac {1}{2}}tanh\left({\dfrac {x-\mu }{2s}}\right)}$, onde ${\displaystyle x,\mu \in R}$ e ${\displaystyle s>0}$.

Função quantil

A inversa da função distribuição é designada por função quantil, sendo representada por:

${\displaystyle Q(p;\mu ,s)=\mu +slog\left({\dfrac {p}{1-p}}\right)}$, onde ${\displaystyle x,\mu \in R}$, ${\displaystyle s>0}$ e ${\displaystyle 0<p<1}$.

Note-se que a função quantil é uma generalização da função logit. Assim, a função quantil pode ser reescrita obtendo-se

${\displaystyle Q(p;\mu ,s)=\mu +slogit(p)}$, onde ${\displaystyle 0<p<1}$.

Além disso, a derivada da função quantil é dada por

${\displaystyle Q'(p;\mu ,s)={\dfrac {s}{p(1-p)}}}$, onde ${\displaystyle x,\mu \in R}$, ${\displaystyle s>0}$ e ${\displaystyle 0<p<1}$.

Parametrização alternativa

Uma parametrização alternativa pode ser feita se considerar que o parâmetro ${\displaystyle s}$ possa ser substituído por ${\displaystyle q\sigma }$, onde ${\displaystyle q={\dfrac {\sqrt {3}}{\pi }}}$; e ${\displaystyle \sigma }$ passa a ser o novo parâmetro a ter em conta.

Assim, a f.d.p. e a função distribuição para a variável aleatória ${\displaystyle X}$ podem ser reescritas, respetivamente, tendo em conta as seguintes expressões:

${\displaystyle f(x;\mu ,s)={\dfrac {\pi }{\sigma {\sqrt {3}}}}{\dfrac {e^{-\left({\dfrac {\pi (x-\mu )}{\sigma {\sqrt {3}}}}\right)}}{\left[1+e^{-\left({\dfrac {\pi (x-\mu )}{\sigma {\sqrt {3}}}}\right)}\right]^{2}}}}$ e ${\displaystyle F(x;\mu ,s)={\dfrac {1}{1+e^{-\left({\dfrac {\pi (x-\mu )}{\sigma {\sqrt {3}}}}\right)}}}}$, onde para ambas ${\displaystyle x,\mu \in R}$ e ${\displaystyle \sigma >0}$.

Propriedades

As propriedades mais importantes de uma distribuição dizem respeito ao valor esperado (também designado por esperança ou média), variância, moda, mediana e função geradora de momentos. Assim, considerando a variável aleatória ${\displaystyle X}$, as propriedades desta são dadas pelas seguintes expressões, respetivamente ^{[2] [3]}:

${\displaystyle E(X)=\int \limits _{-\infty }^{\infty }\displaystyle xf(x)=\int \limits _{-\infty }^{\infty }\displaystyle {\dfrac {xe^{-\left({\dfrac {x-\mu }{s}}\right)}}{s\left[1+e^{-\left({\dfrac {x-\mu }{s}}\right)}\right]^{2}}}=\mu }$

${\displaystyle V(X)=E(X)-(E(X))^{2}=\int \limits _{-\infty }^{\infty }\displaystyle {\dfrac {x^{2}e^{-\left({\dfrac {x-\mu }{s}}\right)}}{s\left[1+e^{-\left({\dfrac {x-\mu }{s}}\right)}\right]^{2}}}-\mu ^{2}={\dfrac {s^{2}\pi ^{2}}{3}}}$

${\displaystyle Moda=Mediana=\mu }$

${\displaystyle M(t)=e^{\mu t}\Gamma ({1-st})\Gamma ({1+st}),|t|<{\dfrac {1}{s}}}$

Note-se que na expressão da função geradora de momentos, a letra ${\displaystyle \Gamma }$ designa a função gama.

Outras duas propriedades que não são muito estudadas são a assimetria e a curtose. A assimetria é uma propriedade que referencia a assimetria da distribuição; e para este caso, a medidade de assimetria é ${\displaystyle 0}$, uma vez que a distribuição logística é simétrica ^[4]. Enquanto a curtose é uma medida de forma que caracteriza o achatamento da curva da f.d.p. das distribuições. Para a distribuição em causa, o valor da curtose é ${\displaystyle 1,2}$ ^[4]. Pelo facto da f.d.p. desta distribuição ser muito semelhante à f.d.p. da distribuição normal, o valor da curtose, ao ser um valor positivo maior que zero, significa que a distribuição logística é mais alta e afunilada que a distribuição normal .

Aplicações

A distribuição logística foi investigada pela primeira vez pelo matemático francês Pierre Verhulst nas décadas de 1830 e 1840; e recebeu seu nome num artigo de 1929 de Reed e Berkson ^[5]. Embora o interesse original de Verhulst tenha sido no estudo da demografia e na modelagem de populações humanas, um dos principais usos da distribuição logística historicamente tem sido em estatística, como uma ferramenta, na chamada regressão logística ^[5].

Ainda hoje, no entanto, a distribuição logística é uma ferramenta frequentemente utilizada na análise de sobrevivência, onde é preferível sobre distribuições qualitativamente similares, por exemplo, à distribuição normal ^[5]. As ferramentas derivadas e inspiradas pela distribuição logística são geralmente usadas para representar dados de tolerância em várias ciências da vida, incluindo zoologia e fisiologia; e a própria distribuição é usada em finanças matemáticas para modelar o risco de vários ativos financeiros ^[5]. A distribuição logística também pode modelar uma série de fenômenos, incluindo a disseminação de doenças, crescimento celular e a disseminação de inovações ^[5].

Um facto interessante é que a Federação de Xadrez dos Estados Unidos e a Federação Mundial de Xadrez (FIDE) usam a distribuição logística para calcular o nível de habilidade relativa dos jogadores de xadrez ^[4]. Anteriormente, ambos usavam a distribuição normal ^[4].

Aplicação no software R

Figura 4 — Gráfico da f.d.p. para a sequência definida

Figura 6 — Gráfico da função distribuição para a sequência definida

No software R,^{[necessário esclarecer]} para usar a distribuição logística, é necessária a instalação do package stats que contém os comandos referentes à f.d.p., à função distribuição e à função quantil ^[6]. Além disso, também é possível gerar números aleatórios que seguem esta distribuição ^[6]. Para se usar os comandos, é crucial definir primeiro os parâmetros de localização e escala. Note-se que se estes parâmetros não forem definidos previamente, o software R assume por defeito que o parâmetro de localização é ${\displaystyle 0}$ e o parâmetro de escala é ${\displaystyle 1}$.

Existindo um package que contém as funções essenciais da distribuição logística, não é necessário o utilizador definir essas funções. No entanto, para exemplos ilustrativos, realizou-se um pequeno exercício que demonstra que aodefinir a função ou utilizar os comandos do R, para um determinado valor de uma sequência, os resultados são iguais. Os scripts do R encontram-se nas Figuras 3, 5, 7 e 8.

Suponha-se que se considera os parâmetros de localização e escala definidos por ${\displaystyle \mu =2}$ e ${\displaystyle s=1}$, respetivamente, e define-se ${\displaystyle x}$ como sendo uma sequência de valores entre ${\displaystyle -10}$ e ${\displaystyle 10}$ de tamanho ${\displaystyle 100}$. Caso o utilizador queira definir ele próprio a f.d.p., deve utilizar o comando function() e inserir a expressão correspondente. Através do comando plot(), pode-se ter acesso ao gráfico da f.d.p. definida para a sequência de valores de ${\displaystyle x}$. No script da Figura 3, definiu-se a função da f.d.p., fez-se o gráfico desta função que pode ser visto na Figura 4 e, por fim, para um valor da sequência, ${\displaystyle x=6}$, determinou-se o valor da função neste ponto. Em seguida, utilizou-se o comando do R, dlogis(), que representa a f.d.p. já definida pelo próprio software; e calculou-se também para o mesmo valor da sequência definido anteriormente. É espectável que, estando todos os comandos bem definidos, o valor é exatamente igual. Assim, considerando ambos os comandos, o valor da f.d.p., para ${\displaystyle x=6}$, é dado por ${\displaystyle 0,0177}$.

Figura 3 — Script da f.d.p.

Realizou-se o mesmo processo para a função distribuição. O comando do R para esta função é designado por plogis(). O valor da sequência escolhido foi ${\displaystyle 5}$. E, tal como seria de esperar, para ambos os comandos, o valor da função distribuição para ${\displaystyle x=5}$ é dado por ${\displaystyle 0,9526}$. Na Figura 5, visualiza-se o script do R para a função distribuição; e o gráfico desta função, para a sequência de valores definida no script, encontra-se na Figura 6.

Figura 5 — Script da função distribuição

Figura 9 — Gráfico da função quantil para a sequência definida

A função quantil é representada pelo comando qlogis(). Uma vez que esta função é definida por um logaritmo, ela apenas calcula quantis para valores entre ${\displaystyle 0}$ e ${\displaystyle 1}$. Definiu-se a função quantil também pelo comando function() e, para fazer a sua representação gráfica, considerou-se uma sequência de valores para ${\displaystyle p}$ entre ${\displaystyle 0}$ e ${\displaystyle 1}$ de tamanho ${\displaystyle 100}$, tendo obtido a Figura 9. Em seguida, calculou-se o 1º Quartil, para ${\displaystyle p={\dfrac {1}{4}}}$; a mediana, para ${\displaystyle p={\dfrac {1}{2}}}$; e o 3º Quartl, para ${\displaystyle p={\dfrac {3}{4}}}$, usando o comando já existente no R e a função definida, com parâmetros dados por ${\displaystyle \mu =2}$ e ${\displaystyle s=1}$. Na Figura 8, encontra-se o script do R para a função quantil. Assim, para o 1º Quartil, obteve-se uma quantil de ${\displaystyle 0,9014}$; para a mediana, um quantil de ${\displaystyle 2,0000}$; e, para o 3º Quartil, um quantil de ${\displaystyle 3,0986}$, usando ambos os comandos.

Figura 8 — Script da função quantil

Figura 7 — Script da geração de números aleatórios

Para os exemplos anteriores, considerou-se um valor inicial fixo. No entanto, o comando rlogis() permite gerar valores aleatórios da distribuição em causa para um determinando conjunto de observações. No script do R da Figura 7, gerou-se ${\displaystyle 100}$ observações da distribuição logística, com parâmetros ${\displaystyle 4}$ e ${\displaystyle 2}$ para a localização e escala, respetivamente.

Todas as distribuições possuem um package, que utilizando o software R, o utilizador tem acesso às funções que lhes são correspondentes. Assim, uma vez que todas as distribuições são cruciais para diversos estudos, graças a esses packages não é necessário que o utilizador perca tempo em definir cada uma das funções.

Referências

1. Viali, Lorí. «Modelos Probabilísticos Contínuos» (PDF) ^{[ligação inativa]}
2. «RPubs - Logistics Distribution Basics». rpubs.com
3. Oliveira, Anderson Castro. «Lista de Modelos Probabilísticos» (PDF). Lista de Modelos Probabilísticos
4. «Logistic Distribution». Statistics How To (em inglês)
5. «LogisticDistribution—Wolfram Language Documentation». reference.wolfram.com (em inglês)
6. «R: The Logistic Distribution». stat.ethz.ch