Półokrąg

Półokrąg – łuk okręgu wyznaczony przez kąt środkowy o mierze 180°. Końce półokręgu leżą więc na jednej średnicy. Promieniem półokręgu jest promień okręgu, którego częścią jest półokrąg.

Rys. 1. Punkt B poruszający się po półokręgu (łuku ABC) będącym częścią okręgu o środku O. Końce tego półokręgu leżą na odcinku AC. Odcinek AB to promień wodzący punktu B względem punktu A. Odcinek CB to promień wodzący punktu B względem punktu C. Kąt ABC oparty na średnicy AC jest prosty (zob. twierdzenie Talesa).

Rys. 2

Twierdzenie o kącie wpisanym w półokrąg

Osobny artykuł: Twierdzenie Talesa.

Twierdzenie to, przypisywane Talesowi, mówi że każdy kąt wpisany w półokrąg oparty na jego podstawie jest kątem prostym.

Wyznaczanie średnich

Wykorzystując właściwości półokręgu, można konstrukcyjnie wyznaczyć średnie z dwóch liczb ${\displaystyle a}$ i ${\displaystyle b.}$

Średnia arytmetyczna

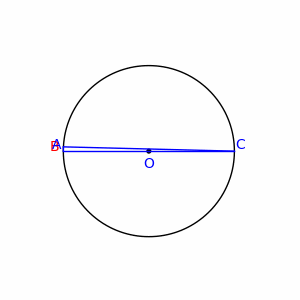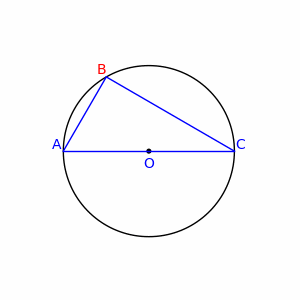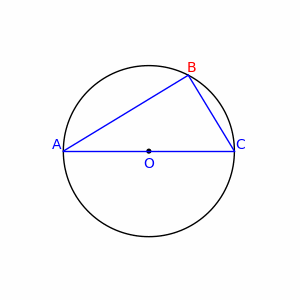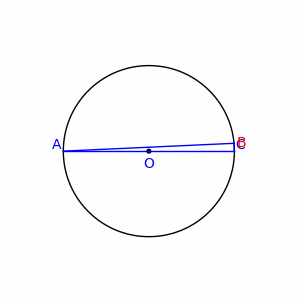
Należy skonstruować półokrąg o podstawie równej ${\displaystyle a+b.}$ Promień tego półokręgu jest średnią arytmetyczną z obu liczb (rys. 2 – czerwona linia)

${\displaystyle c={\frac {a+b}{2}}.}$

Średnia geometryczna

Konstruując półokrąg taki sam jak w poprzednim przykładzie, należy narysować odcinek o początku w miejscu zetknięcia się odcinków o długościach ${\displaystyle a}$ i ${\displaystyle b,}$ prostopadły do podstawy, o końcu leżącym na łuku półokręgu. Długość tego odcinka jest równa średniej geometrycznej liczb ${\displaystyle a}$ i ${\displaystyle b}$ (rys. 2 – brązowa linia)

${\displaystyle d={\sqrt {ab}}.}$

Można to wykazać, wykorzystując twierdzenie Pitagorasa oraz fakt, że kąt oparty na odcinku o długości ${\displaystyle a+b}$ jest kątem prostym.

Zobacz też

• konstrukcje geometryczne

Bibliografia

• Włodzimierz Waliszewski: Encyklopedia szkolna. Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1988, s. 171. ISBN 83-02-02551-8.
• I.N. Bronstein, K.A. Siemiendiajew: Matematyka. Poradnik encyklopedyczny. Wyd. 14. Warszawa: Wydawnictwo Naukowe PWN, 1997. Brak numerów stron w książce

Linki zewnętrzne

• hasło „półokrąg”. [w:] Słownik języka polskiego [on-line]. Wydawnictwo Naukowe PWN SA. [dostęp 2017-05-14].
• hasło „półkole”. [w:] Słownik języka polskiego [on-line]. Wydawnictwo Naukowe PWN SA. [dostęp 2017-05-14].

Encyklopedie internetowe (miejsce geometryczne):

• Catalana: 0141648, 0210114, 0141652