matematiker, fysiker og oppfinner i det antikke Hellas From Wikipedia, the free encyclopedia
Arkimedes (gresk Ἀρχιμήδης; født 287 f.Kr. i Syrakus på Sicilia, død 212 f.Kr.) var en matematiker, fysiker og oppfinner i det antikke Hellas. Selv om lite er kjent fra hans liv og få av hans skrifter er bevart, blir han regnet som en av de viktigste vitenskapsmenn i den klassiske antikken. I tillegg til at han gjorde viktige oppdagelser innenfor matematikk og geometri, har han fått æren for å ha laget maskiner og innretninger som var langt forut for sin tid.[7]
| Arkimedes fra Syrakus (Gresk: Ἀρχιμήδης) | |||
|---|---|---|---|
 «Tankefull Arkimedes» av Domenico Fetti (1620) | |||
| Født | Ἀρχιμήδης ca. 287 f.Kr.[1][2][3][4] ancient Syracuse | ||
| Død | 212 f.Kr.[2][5][6][3] ancient Syracuse | ||
| Beskjeftigelse | Matematiker, fysiker, astronom, oppfinner, militæringeniør, filosof, ingeniør | ||
| Far | Fidias | ||
| Nasjonalitet | ancient Syracuse | ||
| Region | Klassisk gresk filosofi | ||
| Hovedinteresser | matematikk, fysikk, astronomi | ||
| Ideer | Hydrostatikk, vektstenger, Infinitesimaler | ||
Romerrikets historikere viste stor interesse for Arkimedes og skrev flere biografier om hans liv og virke, og de få kopiene som ble bevart av hans avhandlinger skulle få stor innflytelse på vitenskapsfolk under renessansen.
Arkimedes er blant folk flest mest kjent å ha oppdaget loven om legemers oppdrift i vann (kjent som Arkimedes lov), mens han blant sine etterfølgere innenfor matematikken nok er mest kjent for å ha vært den første som gjorde en summering av en uendelig rekke med en metode som er i bruk fortsatt.

Arkimedes ble født rundt år 287 f.kr. i havnebyen Syrakus på Sicilia, som da var en koloni for Magna Graecia. Fødselsåret er beregnet ut ifra den bysantinske lærde Johannes Tzetzes opplysninger om at han var 75 år da han døde. I verket ψαμμιτης (Psammites) oppgir Arkimedes Fidolos som sin fars navn, han skal ha vært astronom men utover dette er ingenting kjent om ham. Plutark skrev at Arkimedes var i slekt med kong Hiero II av Syrakus. En biografi om Arkimedes skal ha blitt skrevet av en venn av ham ved navn Herakleides, men denne er gått tapt og vi har ingen samtidige kilder om Arkimedes' liv. Det er f.eks. ikke kjent om han var gift eller hadde barn. Det er antatt at Arkimedes tilbrakte deler av sin ungdom i Alexandria i Egypt, hvor han i tilfelle var samtidig som Konon fra Samos og Eratosthenes. Denne underbygges av at noen av Arkimedes' matematiske arbeider ble skrevet i form av brev til Eratosthenes, som var sjefsbibliotekar i Alexandria.
Arkimedes døde 212 f.Kr. da Syrakus ble inntatt av romerske styrker under Marcus Claudius Marcellus etter to års beleiring. Ifølge den populære versjonen fra Plutarks Livsskildringer satt Arkimedes fordypet over et matematisk diagram da byen ble inntatt. En romersk soldat gav ham ordre om å bli med til Marcellus, men Arkimedes nektet og sa han måtte fullføre arbeidet med diagrammet først. Soldaten skal da ha blitt så sint at han drepte Arkimedes med sverdet sitt. Marcellus ble etter sigende rasende da han hørte at Arkimedes hadde blitt drept, siden han hadde gitt ordre om at han skulle spares.
Arkimedes siste ord skal ifølge tradisjonen ha vært «Ikke rør mine sirkler» (på gresk: μή μου τούς κύκλους τάραττε, men oftest gjengitt på latin: Noli turbare circulos meos). Det finnes imidlertid ikke pålitelige bevis for at dette skal være sant.
På Arkimedes grav var hans yndlingsdiagram hugget inn, en framstilling av en kule inni en sylinder med samme høyde og diameter. Arkimedes hadde vist at volumet og overflatearealet av kulen er to tredjedeler av sylinderens volum og areal. I 75 f.Kr. besøkte den kjente romerske taleren Cicero Arkimedes grav i Syrakus, 137 år etter hans død. Graven var da overgrodd, men Cicero fikk den ryddet og renset slik at han kunne se diagrammet og lese versene som hadde blitt føyet til som en inskripsjon.
Beretningen om beleiringen av Syrakus som Polybios gir i sin «Historiene» ble skrevet om lag 70 år etter Arkimedes' død, og var primærkilden for Plutark og Titus Livius. Polybios var opptatt av krigsmaskinene Arkimedes skal ha konstruert, og ikke av Arkimedes som person.

Den mest kjente anekdoten som har blitt fortalt om Arkimedes er om hvordan han oppdaget prinsippet for oppdrift. Ifølge Vitruvius skulle kong Hieron II ha fått en ny krone formet som en laurbærkrans, og Arkimedes ble bedt om å fastslå om kronen virkelig var av rent gull, eller om en uærlig gullsmed hadde tilsatt sølv. Arkimedes måtte løse dette problemet uten å skade kronen, så han kunne ikke smelte den for å måle tettheten til materialet i terningform, hvilket ville ha vært den enkelste måten å løse problemet på. Kronens tetthet ville være lavere dersom billigere materialer med mindre tetthet enn gull hadde vært lagt til. Da han tok seg et bad, la han merke til at vannstanden steg da han kom ned i vannet. Han skjønte at denne effekten kunne brukes til å bestemme volumet til kronen, og slik også tettheten dersom han veide den. Han ble så begeistrert over sin egen oppdagelse at han glemte å kle på seg, men sprang ut naken på gaten mens han ropte Eureka! («Jeg har funnet det!»).
Historien om gullkronen finnes ikke i noen av de kjente verkene til Arkimedes, men i sin avhandling Om flytende legemer forklarer han det hydrostatiske prinsippet som i dag er kjent som Arkimedes prinsipp: På et legeme som er senket ned i en væske vil det virke en oppdriftskraft som er like stor som vekten av væsken legemet har presset bort.
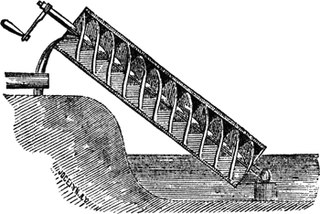
En annen oppfinnelse som bærer hans navn er Arkimedes' skrue, en maskin med et roterende skrueformet blad inni et rør. Innretningen ble drevet med håndmakt, og kunne brukes til å pumpe opp vann. Pumper som er konstruert etter dette prinsippet brukes fortsatt i noen deler av verden, og det samme prinsippet brukes også i gruver og under boring av tunneler for å transportere ut den utgravde masse. Arkimedes' skrue slik den ble beskrevet av Vitruvius kan ha vært en forbedret utgave av innretningen som ble brukt til å vanne Babylons hengende hager.[8] Selv om Arkimedes ikke oppfant vektstangen, ga han de første utførlige beskrivelsene av vektstangprinsippet. Han viste hvordan kraften (dreiemomentet) ville øke proporsjonalt med lengden på vektstangen. Hans vektstanglov sier:
Størrelse er i likevekt på avstander gjensidig proporsjonale til deres vekt.
Ifølge Pappos fra Alexandria skal Arkimedes studier av vektstangprinsippet fått ham til å utbryte: «Gi meg et fast punkt, og jeg skal bevege hele jorden!» Plutark beskriver hvordan Arkimedes utviklet et system med trinser og taljer som lot sjøfolk bruke vektstangprinsippet til å heve gjenstander som ellers ville ha vært alt for tunge til å flytte på.
En stor del av Arkimedes konstruksjoner ble laget ut fra behovene i hans hjemby Syrakus. Athenaios beskriver hvordan kong Hieron hyrte Arkimedes for å tegne det store skipet Syrakusia. Dette skipet skal ha vært 55 meter langt, og det har vært hevdet at det var det største transportskipet i antikken. Ifølge Athenaios hadde det rom for 600 mennesker, og inneholdt hagedekorasjoner, et gresk gymnasium og et tempel viet til Afrodite. Siden et så stort skip bygget med datidens teknologi ville ta inn betydelige mengder vann, skal Arkimedes skrue ha blitt utviklet med det formål for øye å lense Syrakusia.
Det har blitt hevdet at byen Syrakus var i stand til å forsvare seg så lenge mot romerske angrep under den andre punerkrigen først og fremst fordi Arkimedes konstruerte nye og geniale våpen. Av disse er de mest kjente de såkalte Arkimedes' dødsstråle og Arkimedes' klo. Den nøyaktige konstruksjonen av disse våpnene er ikke kjent, men dødsstrålen skal ha vært en innretning som kunne fokusere sollys gjennom speil eller optiske linser mot de romerske skipene og slik sette dem i brann. Arkimedes klo skal ha vært en slags krok med gripehaker festet til en kranlignende konstruksjon. Ved hjelp av denne innretningen skal forsvarerne på bymuren ved havnen ha kunnet løfte og dermed kantre romerske skip. Det er svært usikkert om noen av disse våpnene har eksistert. Mer sannsynlig er det at Arkimedes bidro til tekniske forbedringer av katapulter og lignende.
Arkimedes skal også under første punerkrig ha konstruert verdens første odometer (kilometerteller). Dette skal ha vært en vogn med en innretning som slapp en liten ball i en beholder for hver kilometer som ble tilbakelagt.

Cicero skrev at etter at han hadde erobret Syrakus tok Marcellus med seg to mekaniske innretninger til Roma, og at disse ble brukt som hjelpemidler innen astronomi. Cicero gir Tales fra Milet og Eudoksos æren for å ha konstruert disse instrumentene. Det ene instrumentet viste bevegelsene til solen, månen og fem planeter, og det ble demonstrert for Cicero 150 år senere av en mann ved navn Gallus. Cicero beskriver hendelsen som følger:
Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in [caelo] sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione. – Når Gallus beveget globen, skjedde det at månen fulgte solen så mange ganger på denne bronse [innretningen] som på himmelen selv, fra hvilken også på himmelen solens globe fikk samme omkretsing, og månen kom så til den posisjonen som var skyggen [av den på] jorden når solen var på linje.[9]
Den innretningen Cicero beskriver er mekanisk planetarium. Ifølge Pappos hadde Arkimedes skrevet et manuskrift (som nå er tapt) om konstruksjonen av slike apparater kalt Om å lage glober. Å konstruere slike innretninger krever en omfattende kjennskap til tannhjulteknikk. Det var antatt at slike mekanismer var utenfor rekkevidde for den teknologien som var tilgjengelig i antikken, men funnet av Antikytheramekanismen i 1902 viste at slike konstruksjoner fantes i det antikke Hellas.
Selv om Arkimedes ofte blir betraktet først og fremst som en som konstruerte mekaniske apparater, ga han også svært viktige bidrag innenfor matematikken. Plutark skrev:«Han la hele sin hengivenhet og ambisjon i de renere spekulasjoner hvor det ikke er noen referanse til livets vulgære behov.»

Noen av Arkimedes matematiske bevisføringer inkluderer en bruk av infinitesimaler som ikke er ulik den vi finner i moderne integralregning. Ved å forutsette at en antakelse var sann, og så vise at dette ville føre til en selvmotsigelse, kunne Arkimedes gi svar på til en vilkårlig grad av nøyaktighet, samtidig som han innsnevret området svaret kunne ligge innenfor. Denne innsnevringsmetoden brukte han for å bestemme tallverdien til π (pi). Han gjorde dette ved å tegne to mangekanter (polygoner), en større utenfor en sirkel og en mindre inni sirkelen. Disse lå så tett til sirkelen som mulig, altså slik at både den ytre n-kanten og den indre n-kanten berørte sirkelen n ganger. Etter hvert som han økte antall kanter kom han sammenfalt mangekantene mer og mer med sirkelen. Ved hjelp av 96-kanter klarte han å beregne at verdien til π lå mellom 31/7 og 310/71, altså mellom 3,1429 og 3,1408. Verdien av π uttrykt med ti desimaler er 3,1415926536. Å fastslå π med slik nøyaktighet var en fremragende prestasjon, siden det greske tallsystemet den gang var tungvint og besto av bokstaver i stedet for posisjonsnotasjonen som brukes i dag.
Ved samme innsnevringsmetode kunne Arkimedes beregne verdien til kvadratroten av tallet tre til mellom 265/153 og 1351/780, altså at verdien lå mellom 1,732 og 1,7320512. Den moderne verdien er ca. 1,7320508076, noe som gjør dette til en svært nøyaktig tilnærming.
Arkimedes beviste også at arealet til en sirkel var lik π ganger kvadratet av radiusen.
Et annet kjent matematisk verk av ham er Sand-opptelleren. I dette verket har han satt seg fore å beregne hvor mange sandkorn som universet kan inneholde. Ved å gjøre dette utfordret han ideen om at antallet sandkorn var for stort til å kunne telles. Han skrev: «Det er noen, kong Gelon [Gelon II, sønn av Hieron II] som tror at sand[kornenes] antall er ubestemmelig i mengde.» Ved å tallfeste sandkornene ville han motbevise dette, og han presiserte «Jeg mener med sand ikke bare det som finnes rundt Syrakus og resten av Sicilia, men også det som finnes i ethvert område, enten det er bebodd eller ubebodd.» For å løse problemet utviklet han et system for telling basert på myriader. Myriade ble i gresk språk brukt både om uendelig (det greske ordet for utellelig var murios) og som ti tusen (104. Han foreslo et tellesystem hvor man brukte myriader av myriade som enhet (hundre millioner) og konkluderte med at antall sandkorn måtte være 8 x 1063 (moderne tallnotasjon).
Innenfor geometri beviste Arkimedes at arealet som dannes mellom en parabel og en rett linje er 4/3 av arealet av en trekant med samme grunnlinje og høyde.
Han uttrykte løsningen på dette problemet som en geometrisk uendelig rekke med en ratio på 1/4:
Den første leddet er her trekantens areal, det andre en summen av de to trekantene som dannes ved at man deler den opprinnelige trekantens grunnlinje som vist på illustrasjonen og så videre. Beviset er en variant av den uendelige rekken 1/4 + 1/16 + 1/64 +1/256 + ... som kan summeres til 1/3.
Det har vært foreslått at Arkimedes kan ha kjent til Herons formel for å regne ut arealet av en trekant fra lengden av sidene. Den første kjente referansen til denne formelen er imidlertid Heron av Alexandria sin bok Metrica fra rundt år 60 e.kr.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.