Ortogonalitet

I matematikk er to vektorar ortogonale om dei står vinkelrett på kvarandre. Dei dannar altså ein rett vinkel. Ordet kjem frå gresk ὀρθός (orthos), som tyder «rett» og γωνία (gonia), som tyder «vinkel». Til dømes vil ein undergrunnsbane og gata over vere ortogonale om dei kryssar kvarandre med ein rett vinkel, sjølv om dei ikkje fysisk kryssar kvarandre.

AB og CD er ortogonale til kvarandre.

Definisjonar

Definisjon. To vektorar ${\displaystyle x}$ og ${\displaystyle y}$ i eit indre produktrom ${\displaystyle V}$ er ortogonale om det indre produktet deira ${\displaystyle \langle x,y\rangle }$ er lik null. Denne situasjonen vert skrive som ${\displaystyle x\perp y}$.

Definisjon. To vektor-delrom ${\displaystyle A}$ og ${\displaystyle B}$ i eit indre produktrom ${\displaystyle V}$ vert kalla ortogonale delrom om kvar vektor i ${\displaystyle A}$ er ortogonal til kvar vektor i ${\displaystyle B}$. Det største delrommet som er ortogonalt til eit visst delrom er den ortogonale komplementen.

Definisjon. Ein lineær transformasjon ${\displaystyle T:V\rightarrow V}$ vert kalla ein ortogonal lineær transformasjon dersom det indre produktet er bevart. Altså for alle vektorpar ${\displaystyle x}$ og ${\displaystyle y}$ i det indre produktrommet ${\displaystyle V}$ er,

${\displaystyle \langle Tx,Ty\rangle =\langle x,y\rangle .}$

Dette tyder at ${\displaystyle T}$ bevarer vinkelen mellom ${\displaystyle x}$ og ${\displaystyle y}$, og at lengdene ${\displaystyle Tx}$ og ${\displaystyle x}$ er like.

Fleire vektorar er kalla parvise ortogonale om to av dei er ortogonale, og eit sett av slike vektorar vert kalla eit ortogonalt sett. Parvise ortogonale vektorar som er ulike null er alltid lineært sjølvstendige.

Merk at ofte vert ordet normal nytta i staden for ortogonal, altså at ein vektor står normalt på ein annan vektor. Normal vert òg nytta om einingsvektorane. Eit ortogonalt sett vert kalla ortonormalt om alle vektorane er einingsvektorar.

I euklidske vektorrom

I to- og tredimensjonale euklidske rom er to vektorar ortogonale om prikkproduktet deira er null. Det vil sei at vinkelen mellom dei er 90° eller π/2 radianar. Derfor er ortogonaliteten til vektorar ei generalisering av omgrepet vinkelrett. I eit euklidsk delrom er den ortogonale komplementen til ei linje planet som er vinkelrett på linja og omvendt. Merk at dette ikkje samsvarar med omsyn til vinkelrette plan, sidan vektorar i delrom startar frå origo.

I eit firedimensjonalt euklidsk rom er den ortogonale komplementen til ei linje eit hyperplan og omvendt.

Ortogonale funksjonar

Det er vanleg å nytte det følgjande indre produktet for to funksjonar f og g:

${\displaystyle \langle f,g\rangle _{w}=\int _{a}^{b}f(x)g(x)w(x)\,dx.}$

Her introduserer vi ein ikkje-negativ vektfunksjon ${\displaystyle w(x)}$ i definisjonen av dette indre produktet.

Vi seier at funksjonar er ortogonale om det indre produktet deira er null:

${\displaystyle \int _{a}^{b}f(x)g(x)w(x)\,dx=0.}$

Vi skriv normene med omsyn til dette indre produktet og vektfunksjonen som

${\displaystyle \|f\|_{w}={\sqrt {\langle f,f\rangle _{w}}}}$

Medlemmer av ei følgje { f_i : i = 1, 2, 3, ... } er:

• ortogonale visst

${\displaystyle \langle f_{i},f_{j}\rangle =\int _{-\infty }^{\infty }f_{i}(x)f_{j}(x)w(x)\,dx=\|f_{i}\|^{2}\delta _{i,j}=\|f_{j}\|^{2}\delta _{i,j}}$

• ortonormale visst

${\displaystyle \langle f_{i},f_{j}\rangle =\int _{-\infty }^{\infty }f_{i}(x)f_{j}(x)w(x)\,dx=\delta _{i,j}}$

der

${\displaystyle \delta _{i,j}=\left\{{\begin{matrix}1&\mathrm {visst} \ i=j\\0&\mathrm {visst} \ i\neq j\end{matrix}}\right.}$

er Kroneckerdeltaet. Med andre ord er kvart par ortogonale og norma til kvar av dei er 1 når ein har ei ortonormal følgje.

Døme

• Vektorane (1, 3, 2), (3, −1, 0), (1/3, 1, −5/3) er ortogonale til kvarandre, sidan (1)(3) + (3)(−1) + (2)(0) = 0, (3)(1/3) + (−1)(1) + (0)(−5/3) = 0, (1)(1/3) + (3)(1) − (2)(5/3) = 0. Merk òg at prikkproduktet til vektorane med seg sjølv er normene til desse vektorane, så for å sjekke om dei er ortogonale, treng ein berre sjekke prikkproduktet mot dei andre vektorane.
• Vektorane (1, 0, 1, 0, ...)^T og (0, 1, 0, 1, ...)^T er ortogonale til kvarandre. Det er tydeleg at prikkproduktet mellom desse er 0. Vi kan då generalisere dette ved å sjå på vektorar i Z₂ⁿ:

${\displaystyle \mathbf {v} _{k}=\sum _{i=0 \atop ai+k<n}^{n/a}\mathbf {e} _{i}}$

for positive tal a, og for 1 ≤ k ≤ a − 1, er desse vektorane ortogonale, til dømes er (1, 0, 0, 1, 0, 0, 1, 0)^T, (0, 1, 0, 0, 1, 0, 0, 1)^T, (0, 0, 1, 0, 0, 1, 0, 0)^T ortogonale.

• Ta to kvadratfunksjonar 2t + 3 og 5t² + t − 17/9. Desse funksjonane er ortogonale med omsyn til ein einingsvektfunksjon på intervallet frå −1 til 1. Produktet av desse to funksjonane er 10t³ + 17t² − 7/9 t − 17/3, og då

${\displaystyle \int _{-1}^{1}\left(10t^{3}+17t^{2}-{7 \over 9}t-{17 \over 3}\right)\,dt=\left[{5 \over 2}t^{4}+{17 \over 3}t^{3}-{7 \over 18}t^{2}-{17 \over 3}t\right]_{-1}^{1}}$

${\displaystyle =\left({5 \over 2}(1)^{4}+{17 \over 3}(1)^{3}-{7 \over 18}(1)^{2}-{17 \over 3}(1)\right)-\left({5 \over 2}(-1)^{4}+{17 \over 3}(-1)^{3}-{7 \over 18}(-1)^{2}-{17 \over 3}(-1)\right)}$

${\displaystyle ={19 \over 9}-{19 \over 9}=0.}$

• Ortogonalitet mellom cosinus og sinus

cos og sin.

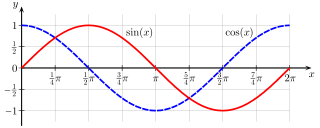
For å syna at cosinus og sinus er ortogonale funksjonar integrerer vi produktet av cosinus og sinus over ein periode (frå 0 til ${\displaystyle 2\pi }$ rad):

${\displaystyle \int _{0}^{2\pi }\cos(\theta )\sin(\theta )d\theta }$.

Vi splittar opp integralet i fire integral, kvar over ein kvart periode:

${\displaystyle \int _{0}^{\pi /2}\cos(\theta )\sin(\theta )d\theta =A_{1},}$

${\displaystyle \int _{\pi /2}^{\pi }\cos(\theta )\sin(\theta )d\theta =A_{2}=-A_{1},}$

${\displaystyle \int _{\pi }^{3\pi /2}\cos(\theta )\sin(\theta )d\theta =A_{3},}$

${\displaystyle \int _{3\pi /2}^{2\pi }\cos(\theta )\sin(\theta )d\theta =A_{4}=-A_{3},}$

så ${\displaystyle A_{1}+A_{2}=0}$ og ${\displaystyle A_{3}+A_{4}=0}$.
Q.E.D.

Kjelder

• Denne artikkelen bygger på «Ortogonality» frå Wikipedia på engelsk, den 23. juli 2009.