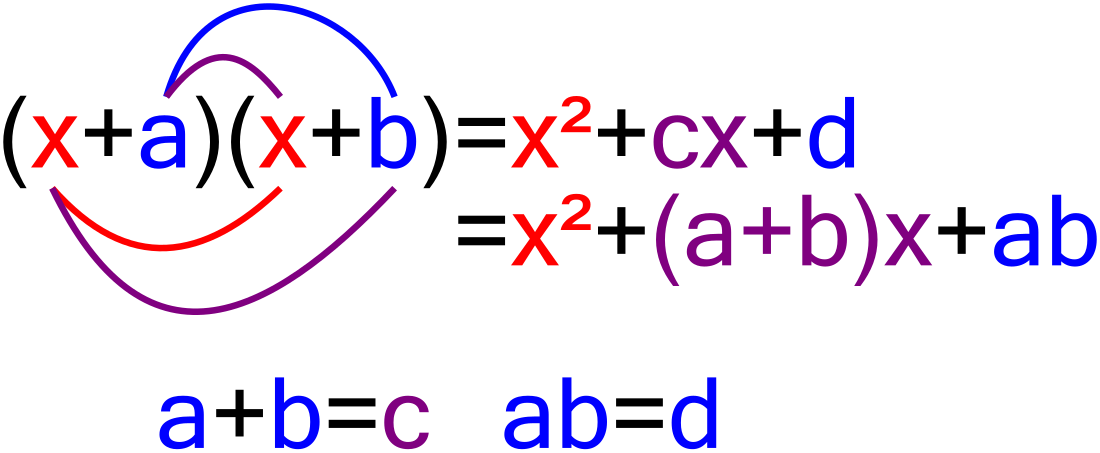Som-product-methode

De som-product-methode of product-som-methode is een eenvoudige methode voor het ontbinden in factoren van een tweedegraads polynoom. Het is een snelle manier om de nulpunten van het polynoom te bepalen. Het is mede daarom dat deze methode samen met de merkwaardige producten aan het begin van de middelbare school bij wiskunde wordt onderwezen.

De nulpunten van een tweedegraads polynoom kunnen niet altijd gemakkelijk met de som-product-methode worden gevonden. Men gebruikt in dergelijke gevallen de abc-formule om de nulpunten te vinden.

Principe

Ieder tweedegraadse polynoom ${\displaystyle f}$ in de variabele ${\displaystyle x}$ is te schrijven als

${\displaystyle f(x)=ax^{2}+bx+c}$

De basisvariant van de som-product-methode gaat ervan uit dat ${\displaystyle a=1}$, zodat

${\displaystyle f(x)=x^{2}+bx+c}$

De ontbinding van ${\displaystyle f}$ in lineaire factoren ziet er dan uit als

${\displaystyle f(x)=(x+w_{1})(x+w_{2})}$

Gelijkstellen van deze twee vormen levert:

${\displaystyle x^{2}+bx+c=(x+w_{1})(x+w_{2})=x^{2}+(w_{1}+w_{2})x+w_{1}w_{2}}$

De som-product-methode berust op het bepalen van ${\displaystyle w_{1}}$ en ${\displaystyle w_{2}}$ door het gelijkstellen van de coëfficiënten:

${\displaystyle w_{1}+w_{2}=b}$

en

${\displaystyle w_{1}w_{2}=c}$

Voor gehele ${\displaystyle w_{1}}$ en ${\displaystyle w_{2}}$ zijn deze vaak met hoofdrekenen te achterhalen.

De nulpunten van ${\displaystyle f}$ zijn ${\displaystyle -w_{1}}$ en ${\displaystyle -w_{2}}$.

Voorbeeld

Voor het ontbinden van het polynoom

${\displaystyle f(x)=x^{2}+2x-15}$

zoekt men twee getallen met som 2 en product –15. Getallen die hieraan voldoen zijn 5 en –3. Dus is

${\displaystyle x^{2}+2x-15=(x+5)(x-3)}$

De nulpunten van ${\displaystyle f}$ zijn daarom ${\displaystyle x=-5}$ en ${\displaystyle x=3}$.

Uitbreiding

De som-product-methode kan worden aangepast voor het geval dat ${\displaystyle a}$ ongelijk is aan 1. Men vermenigvuldigt hiertoe de vergelijking met ${\displaystyle a}$. Zo wordt

${\displaystyle ax^{2}+bx+c=0}$

omgeschreven tot

${\displaystyle a(ax^{2}+bx+c)=a^{2}x^{2}+abx+ac=(ax)^{2}+b(ax)+ac=0}$

Gezocht worden twee getallen ${\displaystyle w_{1}=ax_{1}}$ en ${\displaystyle w_{2}=ax_{2}}$, waarvoor geldt:

${\displaystyle w_{1}+w_{2}=b}$

en

${\displaystyle w_{1}w_{2}=ac}$

Voorbeeld

Voor het oplossen van

${\displaystyle 2x^{2}+7x+6=0}$

schrijven we deze vergelijking als

${\displaystyle 4x^{2}+14x+12=0}$

We zoeken getallen ${\displaystyle w_{1}}$ en ${\displaystyle w_{2}}$, met

${\displaystyle w_{1}+w_{2}=7}$

en

${\displaystyle w_{1}w_{2}=12}$

De getallen 3 en 4 voldoen hieraan, dus is

${\displaystyle 0=4x^{2}+14x+12=(2x+3)(2x+4)}$

met als oplossingen:

${\displaystyle x_{1}=-{\tfrac {3}{2}}\ }$ en ${\displaystyle \ x_{2}=-2}$

Websites

• H Hofstede. De Som- en Productmethode.