Middelpuntshoek en omtrekshoek

Middelpuntshoeken en omtrekshoeken zijn hoeken in en op cirkels. Een middelpuntshoek van een cirkel is een hoek waarvan het hoekpunt samenvalt met het middelpunt van de cirkel. Een omtrekshoek van een cirkel is een hoek waarvan het hoekpunt op de cirkel ligt en de benen gevormd worden door twee koorden.

Middelpuntshoek α en omtrekshoek β

Men zegt dat de hoeken staan op een cirkelboog. In het voorbeeld zien we middelpuntshoek α staan op cirkelboog AB en omtrekshoek β op cirkelboog DC.

Hoofdeigenschap van middelpunts- en omtrekshoeken

Een omtrekshoek is half zo groot als de middelpuntshoek die op dezelfde boog staat.

Het bewijs hiervan wordt gegeven door gevalsplitsing. Er zijn drie mogelijkheden. Het bewijs volgt erg gemakkelijk uit de tekeningen.

• 
  1. Het middelpunt van de cirkel ligt op een been van de omtrekshoek.
• 
  2. Het middelpunt van de cirkel ligt tussen de benen van de omtrekshoek.
• 
  3. Het middelpunt van de cirkel ligt buiten de benen van de omtrekshoek.

Bewijs:

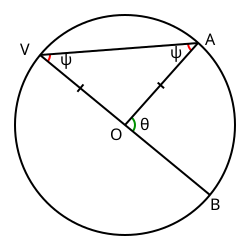
1. Driehoek OAV is gelijkbenig zodat de basishoeken gelijk zijn. De nevenhoek van θ is dus 180°-2ψ, θ = 180°-(180°-2ψ) = 2ψ.
2. Teken de rechte VO zoals in afbeelding 2. Nu volgt uit (1.) dat θ₁ = 2ψ₁ en dat θ₂ = 2ψ₂ zodat θ₀ = θ₁ + θ₂ = 2ψ₁ + 2ψ₂ = 2ψ₀.
3. Teken de rechte VO zoals in afbeelding 3. Uit (1.) volgt dan dat θ₀ = 2ψ₀ en dat θ₁ = 2ψ₁ zodat θ₂ = θ₀ - θ₁ = 2ψ₀ - 2ψ₁ = 2ψ₂.

Q.E.D.

Afgeleide eigenschappen

Rechte hoek Zie Stelling van Thales (cirkels) voor het hoofdartikel over dit onderwerp. Een omtrekshoek die op een halve cirkel staat, is recht. Bewijs: Dit volgt onmiddellijk uit de hoofdeigenschap. 2β = α = 180° zodat β = 90° Q.E.D.
Omtrekshoeken op dezelfde boog (omtrekshoekstelling) Omtrekshoeken die op dezelfde boog staan, zijn even groot. Deze eigenschap wordt o.a. toegepast bij het uitvoeren van de achterwaartse insnijding. Bewijs: Uit de hoofdeigenschap volgt: θ = 2α en θ = 2β en θ = 2ε zodat α = β = ε Q.E.D.
Overstaande hoeken van een koordenvierhoek De overstaande hoeken van een koordenvierhoek zijn supplementair. Bewijs: Uit de hoofdeigenschap volgt dat 2β = α en dat 2ψ = θ zodat 360° = α + θ = 2β + 2ψ = 2(β + ψ) waaruit volgt dat β + ψ = 180°. Het bewijs voor het andere paar overstaande hoeken is volledig analoog. Q.E.D.