Lorenz-aantrekker

De Lorenz-aantrekker (genoemd naar Edward Lorenz) is een fractaal met de vorm van een lemniscaat die overeenkomt met het gedrag op lange termijn van het dynamische systeem van Lorenz (ook wel bekend als de "Lorenz-oscillator") en tevens een van de mogelijke vormen van een vreemde aantrekker.

Vergelijkingen

Het traject van een Lorenz-oscillator voor de waarden ρ = 28, σ = 10, β = 8/3

Een traject van de Lorenz-vergelijkingen, hier weergegeven als een metalen draad om de richting en de 3D-structuur te verduidelijken

Traject met toegevoegde schalen

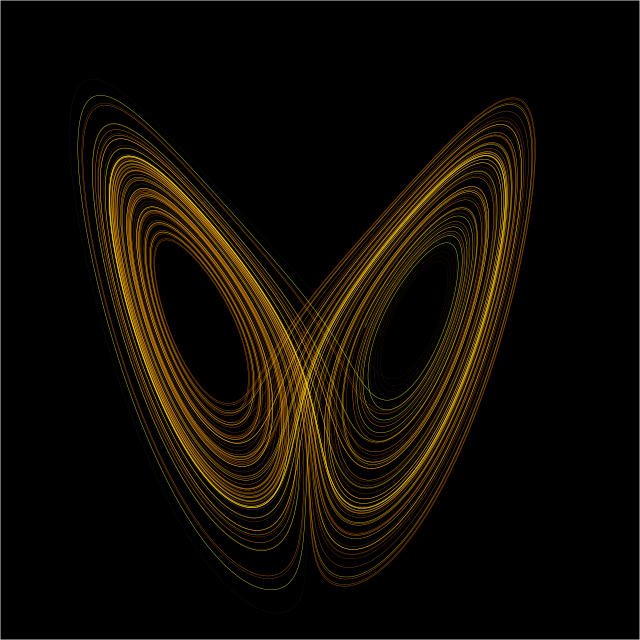
Het gedrag van de Lorenz-oscillator kan worden beschreven door de volgende gewone differentiaalvergelijkingen:

${\displaystyle {\frac {dx}{dt}}=\sigma (y-x)}$

${\displaystyle {\frac {dy}{dt}}=x(\rho -z)-y}$

${\displaystyle {\frac {dz}{dt}}=xy-\beta z}$

Hierin is ${\displaystyle \sigma }$ het getal van Prandtl en ${\displaystyle \rho }$ het getal van Rayleigh. Er geldt ${\displaystyle \sigma }$, ${\displaystyle \rho }$, ${\displaystyle \beta }$ > 0, maar doorgaans neemt men ${\displaystyle \sigma }$ = 10, ${\displaystyle \beta }$ = 8/3 en varieert men ${\displaystyle \rho }$. Bij ${\displaystyle \rho }$ = 28 vertoont het systeem chaotisch gedrag, maar voor andere waarden van ${\displaystyle \rho }$ vertoont het geknoopte periodieke banen. Bij ${\displaystyle \rho =99.96}$ hoort dan bijvoorbeeld een T (3,2) torusknoop.

Illustratie van de sterke afhankelijkheid van de begintoestand
Tijd t=1 (Uitvergroten)	Tijd t=2 (Uitvergroten)	Tijd t=3 (Uitvergroten)
Deze figuren — gebaseerd op de waarden ρ = 28, σ = 10 en β = 8/3 — laten 3 tijdsegmenten zien van de 3-D evolutie van 2 trajecten (blauw en geel) in de Lorenz-aantrekker. De beginpunten van deze trajecten hebben slechts een verschil van 10−5 in de x-coördinaat. Aanvankelijk lijken de twee trajecten samen te vallen (alleen het gele traject is te zien doordat dit over het blauwe heen wordt getrokken), maar na enige tijd lopen ze duidelijk uiteen.
Weergave in Java van de continue evolutie van de Lorenz-aantrekker.

Getal van Rayleigh

De Lorenz-aantrekker voor verschillende ρ-waarden
ρ=14, σ=10, β=8/3 (Vergroten)	ρ=13, σ=10, β=8/3 (Vergroten)
ρ=15, σ=10, β=8/3 (Vergroten)	ρ=28, σ=10, β=8/3 (Vergroten)
Voor kleine waarden van ρ is het systeem stabiel en evolueert het naar een of twee vaste punten. Indien ρ groter is dan 24.28 veranderen de vaste punten in afstoters en wordt het traject op complexe wijze afgestoten, evenwel zonder dat het zichzelf ooit kruist.
Weergave in Java van de evolutie van de verschillende ρ-waarden

Wetenswaardigheden

Hoogleraar Hinke Osinga maakte een haakpatroon om de Lorenz-aantrekker in 3D te visualiseren.

Zie ook

• Mandelbrotverzameling