Cartesisch coördinatenstelsel

"Assenstelsel" verwijst hierheen. Zie Assenstelsel (kristallografie) voor de term uit de kristallografie.

Een cartesisch (of cartesiaans) coördinatenstelsel is een orthogonaal coördinatenstelsel waarbij de afstand tussen twee coördinaatlijnen constant is. Voor elke dimensie is er een as (coördinaatas) die bij twee of drie dimensies onderling loodrecht op elkaar staan. Alle punten in dit stelsel die gegeven (vastgelegd) worden door hun coördinaten ten opzichte van de assen, vormen samen het cartesisch vlak.

Illustratie van een cartesisch coördinaten-stelsel. Vier punten worden gemarkeerd en geëtiketteerd met hun coördinaten. (2,3) in het groen, (-3,1) in het rood, (-1.5, -2.5) in het blauw en de oorsprong (0,0) in het paars.

Het cartesisch stelsel is het meest gebruikte coördinatenstelsel, omdat in dit stelsel meetkundige eigenschappen goed beschreven kunnen worden.

Geschiedenis

Het cartesisch coördinatenstelsel is genoemd naar zijn bedenker, de Franse wiskundige en filosoof René Descartes; diens Latijnse naam was Cartesius.

Descartes ontwikkelde het idee voor dit systeem in 1637 in de volgende publicaties:

• Discours de la méthode
  • In het tweede deel introduceert hij het nieuwe idee om de positie van een punt of een object in een vlak vast te leggen via de afstand daarvan tot twee elkaar snijdende lijnen.
• La Géométrie
  • Hierin werkt hij dat idee verder uit.

Dit assenstelsel werd vervolgens door de Leidse hoogleraar Frans van Schooten uitgewerkt.^[1]

Definitie

Getallenlijn

Zie Reële lijn voor het hoofdartikel over dit onderwerp.

Het kiezen van een cartesisch coördinatenstelsel voor een eendimensionale ruimte - dat wil zeggen voor een rechte lijn - betekent het kiezen van een punt ${\displaystyle O}$, de oorsprong (op die lijn), een eenheid van lengte en een oriëntatie op de lijn. Dit laatste betekent het kiezen welke van de twee halve lijnen die ${\displaystyle O}$ als beginpunt hebben, de positieve en welke de negatieve is. De lijn is dan georiënteerd (of gericht) van de negatieve kant naar de positieve kant. Dan kan de positie van elk punt ${\displaystyle P}$ op de lijn worden vastgelegd door de afstand tot ${\displaystyle O}$, voorzien van een plusteken (+) of minteken (-), afhankelijk van op welke halve lijn ${\displaystyle P}$ ligt.

Een rechte lijn met een gekozen cartesisch systeem wordt getallenlijn genoemd. Elk reëel getal, of het nu een geheel getal, rationaal getal of irrationaal getal is, heeft een unieke positie op de lijn. Omgekeerd kan elk punt op de lijn worden geïnterpreteerd als een getal in een geordend continuüm, dat de reële getallen bevat.

Twee dimensies

Een cartesisch coördinatenstelsel in twee dimensies heeft twee assen, meestal ${\displaystyle x}$-as en ${\displaystyle y}$-as genoemd, die loodrecht op elkaar staan, en een zogeheten assenkruis vormen. De punten in zo'n assenstelsel vormen een vlak, het ${\displaystyle xy}$-vlak of cartesische vlak. De assen worden bij het tekenen meestal horizontaal en verticaal gekozen, met de positieve ${\displaystyle x}$-richting naar rechts en de positieve ${\displaystyle y}$-richting naar boven.

Het punt waarin de twee assen elkaar snijden, wordt oorsprong genoemd, gewoonlijk aangegeven met de letter ${\displaystyle O}$. Op beide assen is de eenheid van lengte gelijk.

Een specifiek punt in het cartesische vlak wordt aangegeven door het coördinatenpaar ${\displaystyle (x,y)}$, gevormd door de coördinaten ${\displaystyle x}$ en ${\displaystyle y}$ van het punt die de gerichte afstanden van het punt tot de beide assen voorstellen. Voorbeeld: het punt (5,2) in de afbeelding hieronder.

Met de pijlen op de assen kan aangegeven worden dat ze oneindig lang zijn in die richting. De twee assen definiëren samen vier kwadranten, aangegeven met de Romeinse cijfers I, II, III en IV. De kwadranten worden tegen de klok in benoemd, beginnend bij het kwadrant rechtsboven. In de onderstaande tabel staan de mogelijke waarden op de ${\displaystyle x}$- en de ${\displaystyle y}$-as voor de vier kwadranten.

kwadrant	${\displaystyle x}$-waarden	${\displaystyle y}$-waarden
I	> 0	> 0
II	< 0	> 0
III	< 0	< 0
IV	> 0	< 0

Drie dimensies

Vroeg in de 19e eeuw is het stelsel uitgebreid naar drie dimensies. Hiervoor is er een nieuwe as geïntroduceerd, de ${\displaystyle z}$-as.

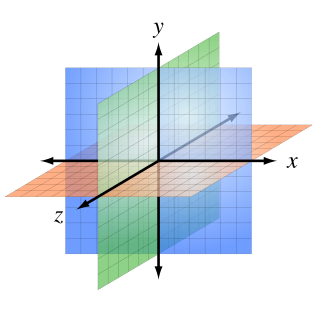
Een punt in een driedimensionale ruimte wordt aangegeven met ${\displaystyle (x,y,z)}$. Een voorbeeld van een driedimensionaal cartesisch coördinatenstelsel is in de hier onderstaande afbeelding te zien. In de afbeelding is het punt (2,3,4) weergegeven.

Oriëntatie

Houding van de rechterhand voor een rechtshandig assenstelsel

In drie dimensies zijn er (afgezien van rotatie van het geheel) twee manieren om de drie assen onderling loodrecht op elkaar te zetten, namelijk via het zogeheten linkshandig of rechtshandig assenstelsel. De afbeelding hierboven is een rechtshandig coördinatenstelsel. Dit kan gecontroleerd worden met de rechterhandregel. Spreid duim, wijs- en middelvinger van de rechterhand zo, dat ze onderling haaks op elkaar staan. De wijsvinger is gestrekt en de middelvinger naar binnen gebogen. Wijs met de wijsvinger in de richting van de positieve ${\displaystyle x}$-as en met de middelvinger in de richting van de positieve ${\displaystyle y}$-as. Als de duim in de richting van de positieve ${\displaystyle z}$-as wijst, is er sprake van een rechtshandig assenstelsel.

Rechtshandig:

Linkshandig:

Wanneer de ${\displaystyle z}$-as naar boven wijst, wordt het soms een wereldcoördinatenstelsel genoemd, zoals in bovenstaande afbeelding. Het belangrijkste is echter in welke richting de assen met hun positieve kant wijzen ten opzichte van elkaar. Het spiegelbeeld van een rechtshandig systeem is een linkshandig systeem.

Het linkshandig systeem wordt ook gebruikt, zij het minder vaak dan het rechtshandig systeem.

Notatie

Het punt ${\displaystyle (0,2,7)}$ in de driedimensionale ruimte kan men een naam geven, bijvoorbeeld ${\displaystyle P=(0,2,7)}$. Of in twee dimensies bijvoorbeeld ${\displaystyle A=({\tfrac {1}{2}},-1)}$. De naam (letter) is slechts een afkorting voor het rijtje getallen. In sommige disciplines bestaat de gewoonte een punt ${\displaystyle P=(x_{P},y_{P},z_{P})}$ niet aan te duiden als het rijtje van z'n coördinaten, maar als ${\displaystyle P(x_{P},y_{P},z_{P})}$, dus met weglating van het =-teken; soms ook met de coördinaten gescheiden door verticale strepen in plaats van door komma's om verwarring met decimale komma's te voorkomen. In die notatie stelt ${\displaystyle B(0|3|1)}$ het punt ${\displaystyle B=(0,3,1)}$ voor.

Transformatie

Een cartesisch coördinatenstelsel kan worden getransformeerd in een ander coördinatenstelsel dat al of niet ook een cartesisch coördinatenstelsel is. Hierbij veranderen de coördinaten van de punten in het assenstelsel. Bijzondere gevallen zijn de transformaties die een lineaire transformatie en/of een isometrie zijn.

Andere coördinatenstelsels waarin de cartesische coördinaten kunnen worden uitgedrukt zijn:

• Poolcoördinaten
• Bolcoördinaten
• Gegeneraliseerde coördinaten

Referentie

• René Descartes (1637): Discourse on Method, Optics, Geometry, and Meteorology; vertaling Paul J. Oskamp (2001).

Zie ook

• Logaritmische schaal
• Euclidische ruimte
• Hilbertruimte

Bronnen, noten en/of referenties

1. Rens Bod (2019): Een wereld vol patronen. Amsterdam: Prometheus; p. 343

Mediabestanden

Zie de categorie Cartesian coordinates van Wikimedia Commons voor mediabestanden over dit onderwerp.