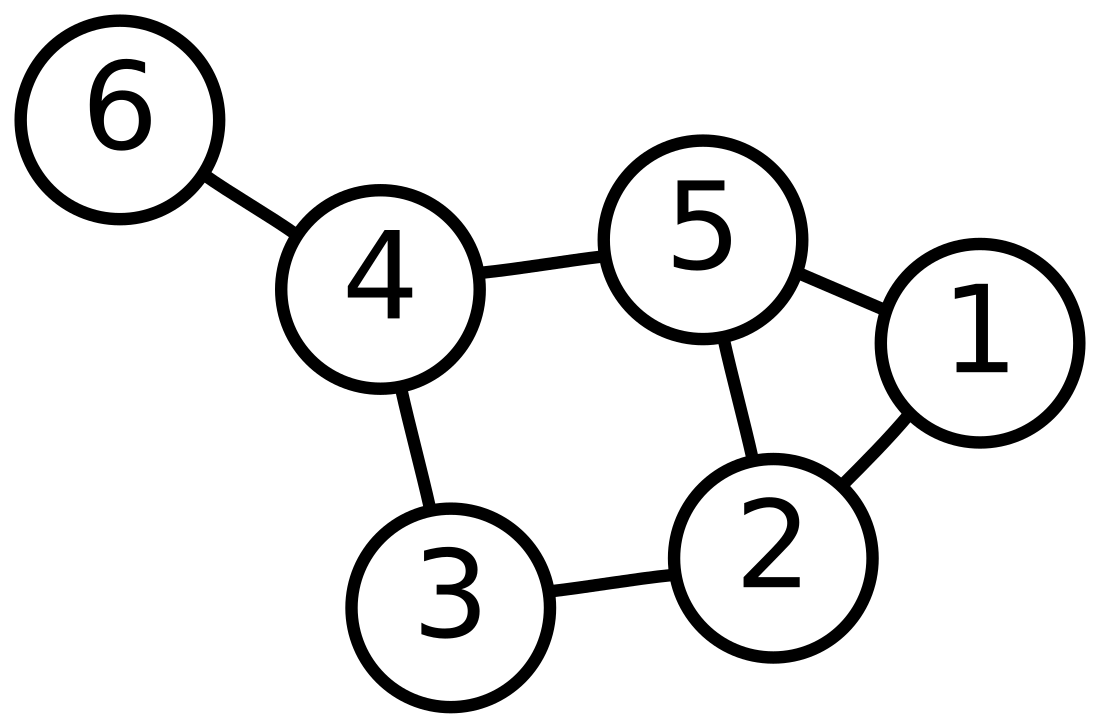
ഒരു ഗണത്തിലെ അംഗങ്ങളിൽ ചിലവ തമ്മിൽ ഏതെങ്കിലും തരത്തിലുള്ള ബന്ധം ഉണ്ടെങ്കിൽ ഈ അംഗങ്ങളും ബന്ധങ്ങളും രേഖപ്പെടുത്താൻ ഉപയോഗിയ്ക്കുന്ന ഒരു വിന്യാസമാണ് ലേഖാസിദ്ധാന്തത്തിലെ (Graph Theory) ലേഖ. ഈ അംഗങ്ങളെ ലേഖയുടെ ശീർഷങ്ങൾ (vertex) എന്നും അവ തമ്മിലുള്ള ബന്ധങ്ങളെ വക്കുകൾ (edge) എന്നും വിളിയ്ക്കുന്നു.[1] ചിത്രരൂപത്തിൽ ശീർഷങ്ങളെ ബിന്ദുക്കളായും വക്കുകളെ രേഖകളോ വക്രങ്ങളോ ആയും വരയ്ക്കുന്നു. ഡിസ്ക്രീറ്റ് മാത്തമാറ്റിക്സിലെ പ്രധാന ആശയങ്ങളിലൊന്നാണ് ഇത്. കേരളത്തിലെ ചില നഗരങ്ങൾ തമ്മിലുള്ള റോഡ് ബന്ധം കാണിയ്ക്കുന്ന ലേഖ വലതുവശത്ത് കാണിച്ചിരിയ്ക്കുന്നു.

ഒരു ലേഖയിലെ വക്കുകൾക്ക് പ്രത്യേക ദിശ ഉണ്ടാവുകയോ ഇല്ലാതിരിയ്ക്കുകയോ ചെയ്യാം. ഉദാഹരണത്തിന് ഒരു പാർട്ടിയ്ക്ക് വന്നിരിയ്ക്കുന്നു ആളുകളെ ഗണമായും അവർ പരസ്പരം കൈ പിടിച്ചു കുലുക്കുന്നുണ്ടോ എന്നത് അവർ തമ്മിലുള്ള ബന്ധം ആയും ചിത്രീകരിയ്ക്കുന്ന ഒരു ലേഖയിൽ വക്കുകൾക്ക് ദിശ ഉണ്ടാകില്ല. A എന്നയാൾ B യുടെ കൈ പിടിച്ചു കുലുക്കുമ്പോൾ B, A യുടെ കൈയും പിടിച്ചു കുലുക്കിയിരിയ്ക്കും. പക്ഷെ ഇതേ പാർട്ടിയിൽ നോക്കൽ ഒരു ബന്ധം ആയി എടുത്താൽ അതിന് ഒരു ദിശ ഉണ്ടായിരിയ്ക്കും. A, B യെ നോക്കി എന്നു പറഞ്ഞാൽ B, A യെയും നോക്കി എന്നർത്ഥമില്ല. വക്കുകൾക്ക് ദിശ ഇല്ലാത്ത ലേഖയെ അദിശലേഖ എന്നും ദിശ ഉള്ളതിനെ സദിശലേഖ എന്നും വിളിയ്ക്കുന്നു.
ലേഖാസിദ്ധാന്തത്തിലെ അടിസ്ഥാനആശയമാണ് ലേഖകൾ. 1878 ൽ ജെയിംസ് ജോസഫ് സിൽവെസ്റ്റർ എന്ന ഗണിതജ്ഞനാണ് "ഗ്രാഫ്" എന്ന വാക്ക് ഈ അർത്ഥത്തിൽ ആദ്യമായി ഉപയോഗിച്ചത്.[2][3]
നിർവ്വചനം

സാമാന്യമായി പറഞ്ഞാൽ G = (V, E) എന്ന ക്രമജോഡിയാണ് ലേഖ.[4] ഇവിടെ V എന്നത് ശീർഷങ്ങളുടെ ഒരു ഗണവും E എന്നത് വക്കുകളുടെ ഒരു ഗണവുമാണ്. E എന്നത് രണ്ടുവീതം അംഗങ്ങളുള്ള V യുടെ ഉപഗണങ്ങളാകുന്നു. (അതായത് രണ്ടു ശീർഷങ്ങൾ തമ്മിൽ യോജിപ്പിച്ചാണ് ഒരു വക്ക് ഉണ്ടാക്കുന്നത്) എന്നാൽ V യുടെ ഇത്തരത്തിലുള്ള എല്ലാ ഉപഗണങ്ങളും E യിൽ ഉണ്ടാകണമെന്നില്ല (അതായത് ഏതു രണ്ട് ശീർഷവും തമ്മിൽ ബന്ധിപ്പിയ്ക്കുന്ന ഒരു വക്ക് ഉണ്ടാകണമെന്ന് നിർബന്ധമില്ല).
സാധാരണയായി V, E എന്നീ ഗണങ്ങൾ പരിമേയമായിട്ടാണ് കണക്കാക്കാറ്. ഇവ അപരിമേയമാണെങ്കിൽ കിട്ടുന്ന ലേഖയുടെ സ്വഭാവം വളരെ വ്യത്യസ്തമായിരിയ്ക്കും. V ശൂന്യഗണമായി എടുക്കാറില്ല, എന്നാൽ E ശൂന്യഗണമാകുന്നതിൽ കുഴപ്പമില്ല. ഒരു ലേഖയുടെ കോടി എന്നത് അതിലെ ശീർഷങ്ങളുടെ എണ്ണമാണ്. അതിന്റെ 'വലിപ്പം' എന്നത് അതിലെ വക്കുകളുടെ എണ്ണം (|E|) ആണ്. ഒരു ശീർഷത്തിന്റെ കൃതി എന്നത് അതിലേയ്ക്ക് ബന്ധപ്പെടുന്ന വക്കുകളുടെ എണ്ണമാണ്. {x, y} എന്ന ലേഖയിലെ ഒരു വക്കിനെ ചുരുക്കി xy എന്ന് രേഖപ്പെടുത്താറുണ്ട്.
മുകളിൽ കൊടുത്തിട്ടുള്ള കേരളത്തിലെ പട്ടണങ്ങളുടെ ലേഖയിൽ V എന്നത് {Ku, T, I, C, Ko} എന്ന ഗണമാണ്. E എന്നത് {(Ku, T), (I, T), (C, T), (C, I), (Ko, I), (Ko, C)} എന്ന ഗണമാണ്. അതിനാൽ ഈ ലേഖയെ ഇങ്ങനെ എഴുതാം :
G = ({Ku, T, I, C, Ko}, {(Ku, T), (I, T), (C, T), (C, I), (Ko, I), (Ko, C)})
അഡ്ജസെൻസി ബന്ധം
G എന്ന ഒരു ആദിശലേഖയിലെ വക്കുകളുടെ ഗണം E അതിന്റെ ശീർഷങ്ങളുടെ ഗണമായ V യിൽ അഡ്ജസെൻസി ബന്ധം അഥവാ ~ എന്ന ഒരു സമമിത ദ്വയാങ്ക ബന്ധം നിർവചിയ്ക്കുന്നുണ്ട്. അതായത് {x, y} എന്ന ഓരോ വക്കിലെയും x, y എന്നീ ശീർഷങ്ങൾ പരസ്പരം അഡ്ജസെന്റ് ആണെന്ന് പറയപ്പെടുന്നു. ഇതിനെ ഇങ്ങനെയും എഴുതാം : x ~ y.
കേരളത്തിലെ പട്ടണങ്ങളുടെ ലേഖയിൽ, ഉദാഹരണത്തിന് : Ku ~ T, അഥവാ കുന്നംകുളവും തൃശ്ശൂരും അഡ്ജസെന്റ് ആണ്. എന്നാൽ കുന്നംകുളവും കൊടുങ്ങല്ലൂരും അഡ്ജസെന്റ് അല്ല.
വിവിധ തരം ലേഖകൾ
അദിശലേഖ
ഒരു ലേഖയിലെ വക്കുകൾക്ക് ദിശ ബാധകമല്ലെങ്കിൽ അതിനെ അദിശലേഖ എന്നു വിളിയ്ക്കുന്നു. അതായത് (x, y) എന്ന വക്കിനു തുല്യമാണ് (y, x) എന്ന വക്കും. വേറൊരു തരത്തിൽ പറഞ്ഞാൽ ഇത്തരം ലേഖയിലെ അഡ്ജസെൻസി ബന്ധം ക്രമരഹിതമാണ്. n ശീർഷങ്ങളുള്ള ഇത്തരം ഒരു ലേഖയിലെ പരമാവധി വക്കുകളുടെ എണ്ണം n(n − 1)/2 ആണ്.
കുന്നംകുളവും തൃശ്ശൂരും തമ്മിൽ ബന്ധപ്പെട്ടിരിയ്ക്കുന്നു എന്ന് പറഞ്ഞാൽ തൃശ്ശൂരും കുന്നംകുളവും തമ്മിലും ബന്ധം ഉണ്ടെന്നർത്ഥം.
സദിശലേഖ


സദിശലേഖ അഥവാ ഡൈഗ്രാഫിലെ വക്കുകൾക്ക് ദിശ ഉണ്ടാകും. ഇതിനെ ഇങ്ങനെ എഴുതാം: G = (V, A). ഇവിടെ :
- V എന്നത് ശീർഷങ്ങളുടെ ഗണമാണ്.
- A എന്നത് ശീർഷങ്ങളുടെ ക്രമജോടികളുടെ ഗണമാണ്. ഇതിലെ ഓരോ ജോടിക്കും ഒരു തുടക്കവും അവസാനവും ഉണ്ടാകും. ഇതിനെ ആരോകൾ/അമ്പടയാളങ്ങൾ എന്നോ ഡിറക്ടഡ് ലൈൻസ് എന്നോ വിളിയ്ക്കുന്നു.
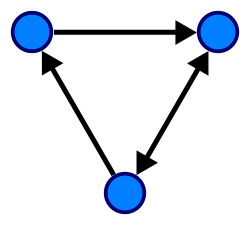
ഉദാഹരണത്തിന് ജന്തുക്കൾ തമ്മിലുള്ള ഭക്ഷ്യശൃംഖല സദിശലേഖയ്ക്ക് ഉദാഹരണമാണ്. പരുന്തിൽ നിന്നും പാമ്പിലേയ്ക്ക് ഒരു ബന്ധം ഉണ്ടെങ്കിലും തിരിച്ച് ഇല്ല. ഈ ഉദാഹരണത്തിൽ V എന്നത് {E, Pm, Pr, K} എന്ന ഗണവും A എന്നത് {(Pr, E), (Pr, K), (Pr, Pm), (Pm, K), (Pm, E)} എന്ന ഗണവും ആണ്.
(x, y) എന്ന അമ്പടയാളം x യിൽ നിന്നും y യിലേക്ക് പോകുന്ന വക്കിനെ സൂചിപ്പിയ്ക്കുന്നു. y നെ ഈ അമ്പടയാളത്തിന്റെ/വക്കിന്റെ തല എന്നും x അതിന്റെ വാൽ എന്നും വിശേഷിപ്പിയ്ക്കുന്നു. x ൽ നിന്നും y ലേയ്ക്ക് നേരിട്ട് ഒരു വക്ക് ഉണ്ടെങ്കിൽ y, x ന്റെ നേരിട്ടുള്ള പ്രീഡെസെസ്സർ ആണെന്ന് പറയുന്നു. x ൽ നിന്നും y ലേയ്ക്ക് മറ്റൊരു ശീർഷം വഴിയേ എത്താനാകൂ എങ്കിൽ y വെറും പ്രീഡെസെസ്സർ ആണെന്ന് പറയുന്നു. G എന്ന സദിശലേഖയിലെ x ൽ നിന്നും y ലേയ്ക്കുള്ള ഓരോ വക്കിനും y ൽ നിന്നും x ലെയ്ക്കും ഒരു വക്ക് ഉണ്ടെങ്കിൽ ആ ലേഖ സമമിതം (symmetric) ആണെന്ന് പറയുന്നു.
മുകളിലെ ഉദാഹരണത്തിൽ (Pm, E) എന്ന അമ്പടയാളത്തിൽ Pm എന്നത് വാലും E എന്നത് തലയും ആകുന്നു.
ഓറിയന്റഡ് ഗ്രാഫ്
ഒരു സദിശലേഖയിലെ വക്കുകളിൽ (x, y), (y, x) ഇവയിൽ ഒന്നു മാത്രമേ ഉള്ളുവെങ്കിൽ അതിനെ ഓറിയന്റഡ് ഗ്രാഫ് എന്നു വിളിയ്ക്കുന്നു. മുകളിലെ ജന്തുക്കളിലെ ഭക്ഷ്യശൃംഖലയെ സൂചിപ്പിയ്ക്കുന്ന സദിശലേഖ ഓറിയന്റഡ് ആണ്.
മിശ്രലേഖ
ഒരു ലേഖയിലെ വക്കുകളിൽ ചിലവയ്ക്ക് ദിശ ഉണ്ടാവുകയും ചിലവയ്ക്ക് ഇല്ലാതിരിയ്ക്കുകയും ചെയ്യുകയാണെങ്കിൽ അതിനെ മിശ്രലേഖ എന്നു വിളിയ്ക്കുന്നു. ഇതിനെ G = (V, E, A) എന്ന ഒരു ട്രിപ്ളേറ്റ് ആയി എഴുതാം. V, E, A എന്നിവയുടെ നിർവചനം മുകളിൽ കൊടുത്തിരിയ്ക്കുന്നു.
മൾട്ടിഗ്രാഫ്
ഒരു ലേഖയിലെ രണ്ടു ശീർഷങ്ങൾക്കിടയിൽ ഒന്നിലധികം വക്കുകൾ ഉണ്ടെങ്കിൽ അതിനെ മൾട്ടി-എഡ്ജ് എന്നു വിളിയ്ക്കുന്നു. ഒരു ശീർഷത്തെ അതിനോട് തന്നെ ബന്ധിപ്പിയ്ക്കുന്ന വക്കുകളെ ലൂപ്പ് എന്ന് വിളിയ്ക്കുന്നു.
മൾട്ടി-എഡ്ജുകളോ ലൂപ്പുകളോ ഉള്ള ഗ്രാഫുകൾ ആണ് മൾട്ടിഗ്രാഫുകൾ.
സിമ്പിൾ ഗ്രാഫ്
അദിശമായ ഒരു ലേഖയിൽ മൾട്ടി-എഡ്ജുകളോ ലൂപ്പുകളോ ഇല്ലെങ്കിൽ അത് സിമ്പിൾ ഗ്രാഫ് ആണ്. ഇത്തരം ലേഖയിൽ n ശീർഷങ്ങളുള്ള ഒരു ലേഖയിൽ ഓരോ ശീർഷത്തിന്റെയും ഡിഗ്രി പരമാവധി n − 1 ആയിരിയ്ക്കും ആയിരിയ്ക്കും.
വെയ്റ്റഡ് ഗ്രാഫ്
ഓരോ വക്കുകൾക്കും അവയുടേതായ ഒരു വെയ്റ്റ് കൊടുത്തിട്ടുണ്ടെങ്കിൽ ആ ലേഖയെ വെയ്റ്റഡ് ഗ്രാഫ് എന്നു വിളിയ്ക്കുന്നു.[5] ഇത് ഏതു പ്രശ്നത്തിന്റെ ലേഖ ആണോ അതിനനുസരിച്ച് ചെലവ്, ദൂരം അങ്ങനെ എന്തുവേണമെങ്കിലും ആകാം. ഉദാഹരണത്തിന് ഒരു സംസ്ഥാനത്തെ പട്ടണങ്ങൾ ശീർഷങ്ങളും അവയുടെ ഇടയിൽ നേരിട്ട് സഞ്ചരിയ്ക്കാമോ എന്നുള്ള വിവരം വക്കുകളും ആയുള്ള ഒരു അടിസ്ഥാന ലേഖ സങ്കൽപ്പിയ്ക്കുക. രണ്ടു പട്ടണങ്ങൾ തമ്മിൽ നേരിട്ടൊരു റോഡ് ഉണ്ടെങ്കിൽ ലേഖയിൽ അവയ്ക്കിടയിൽ ഒരു വക്ക് ഉണ്ടായിരിയ്ക്കും. ഇനി ഈ ലേഖയിൽ അവ തമ്മിലുള്ള ദൂരം കൂടെ വക്കിൽ അടയാളപ്പെടുത്തിയാൽ അതൊരു വെയ്റ്റഡ് ഗ്രാഫ് ആയി. ചില സന്ദർഭങ്ങളിൽ ഇതിനെ നെറ്റ്വർക്ക് എന്നും വിളിയ്ക്കാറുണ്ട്.[6][7]
ക്രമലേഖ
ഒരു ലേഖയിലെ എല്ലാ ശീർഷങ്ങൾക്കും തുല്യ എണ്ണം അയൽക്കാർ ആണുള്ളതെങ്കിൽ അതിനെ ക്രമലേഖ എന്നു വിളിക്കുന്നു. അതായത് ഇത്തരം ലേഖയിൽ എല്ലാ ശീർഷങ്ങളുടെയും ഡിഗ്രി തുല്യമായിരിയ്ക്കും. n അയൽക്കാർ ഉള്ള ഇത്തരം ഒരു ക്രമലേഖയെ n-ക്രമലേഖ എന്നു വിളിയ്ക്കുന്നു. ഉദാഹരണത്തിന് വട്ടത്തിൽ നിന്ന് പരസ്പരം കൈകോർത്തു പിടിച്ചു നൃത്തം ചെയ്യുന്ന ഒരു കൂട്ടം കുട്ടികളെ സൂചിപ്പിയ്ക്കുന്ന ലേഖ ശ്രദ്ധിയ്ക്കുക. ഇവരിൽ ഓരോ കുട്ടിയും അതിന്റെ ഇരുവശത്തുമുള്ള കുട്ടിയുമായി കൈ ചേർത്തു പിടിച്ചിരിയ്ക്കുന്നു. ഈ കൈ ചേർക്കൽ വക്കുകളായി പരിഗണിച്ചാൽ ഓരോ കുട്ടിയ്ക്കും കൃത്യം രണ്ടു കുട്ടികളുമായി ബന്ധമുണ്ട്. അതായത് ഇതൊരു 2-ക്രമലേഖയ്ക്ക് ഉദാഹരണമാണ്.
സമ്പൂർണലേഖ
ഒരു ലേഖയിലെ എല്ലാ ശീർഷങ്ങളും തമ്മിൽ തമ്മിൽ ബന്ധപ്പെട്ടിരിയ്ക്കുന്നുവെങ്കിൽ അതൊരു സമ്പൂർണലേഖയാണ്. സാധ്യമായ എല്ലാ വക്കുകളും ഈ ലേഖയിൽ കാണുന്നു. ഉദാഹരണത്തിന് ഒരു കുടുംബത്തിലെ അംഗങ്ങൾ ശീർഷങ്ങളായും അവർ തമ്മിലുള്ള ബന്ധം വക്കുകളായുമുള്ള ലേഖ എടുത്താൽ ഓരോ ആളും മറ്റെല്ലാ ആളുകളുമായും ബന്ധപ്പെട്ടിരിയ്ക്കുന്നു.
കണക്ടഡ് ഗ്രാഫ്

ഒരു അദിശലേഖയിലെ രണ്ടു ശീർഷങ്ങളാണ് x, y എന്നിരിയ്ക്കട്ടെ. x ൽ നിന്നും y ലേയ്ക്ക് ഒരു പഥം ഉണ്ടെങ്കിൽ (നേരിട്ടോ മറ്റു ശീർഷങ്ങളിലൂടെ കടന്നു പോകുന്നതോ ആയ) {x, y} എന്ന ഗണം കണക്ടഡ് (connected) ആണെന്ന് പറയുന്നു. ഇല്ലെങ്കിൽ അവ ഡിസ്കണക്ടഡ് ആണെന്ന് പറയുന്നു.
ഒരു അദിശലേഖയിലെ ശീർഷങ്ങളെല്ലാം ഇപ്രകാരം കണക്ടഡ് ആണെങ്കിൽ അതിനെ കണക്ടഡ് ഗ്രാഫ് എന്നു വിളിയ്ക്കുന്നു. എന്നാൽ അതിൽ കണക്ടഡ് അല്ലാത്ത ഒരു ശീർഷമെങ്കിലും ഉണ്ടെങ്കിൽ അതിനെ ഡിസ്കണക്ടഡ് ഗ്രാഫ് എന്നു വിളിയ്ക്കുന്നു.
ഉദാഹരണത്തിന് കേരളത്തിലെ പട്ടണങ്ങളുടെ ലേഖ ഒരു കണക്ടഡ് ഗ്രാഫ് ആണ്. എന്നാൽ കേരളത്തിലെയും ലക്ഷദ്വീപിലെയും പട്ടണങ്ങളെ ശീർഷങ്ങളായും അവ തമ്മിലുള്ള റോഡ് ബന്ധങ്ങൾ വക്കുകളായും പരിഗണിച്ചാൽ കിട്ടുന്ന ലേഖ നോക്കുക. തൃശൂർ നിന്നും കവരത്തിയിലേക്ക് ഒരു കണക്ഷൻ ഇല്ലാത്തതിനാൽ ഈ രണ്ടു ശീർഷങ്ങളും ഡിസ്കണക്ടഡ് ആണ്. അതിനാൽ ഈ ലേഖ ഡിസ്കണക്ടഡ് ആണെന്ന് കാണാം.
ഒരു സദിശലേഖയിൽ ഇത് കുറച്ചുകൂടി സങ്കീർണമാണ്. x എന്ന ശീർഷത്തിൽ നിന്നും y എന്ന ശീർഷത്തിലേയ്ക്ക് നയിയ്ക്കുന്ന ഒരു പഥം ഉണ്ടെങ്കിൽ ഇവ രണ്ടും സ്ട്രോങ്ലി കണക്ടഡ് ആണെന്ന് പറയുന്നു. എന്നാൽ ഇങ്ങനെ നയിയ്ക്കുന്ന ഒരു പഥം ഇല്ലെങ്കിൽ അവയ്ക്കിടയിൽ ഉള്ള വക്കുകളുടെ ദിശാസൂചകം എടുത്തുകളഞ്ഞാൽ ഒരു പഥം കിട്ടുമോ എന്നു നോക്കുക. ഇങ്ങനെ ഒന്ന് കിട്ടിയാൽ അവ തമ്മിൽ വീക്ലി കണക്ടഡ് ആണെന്ന് പറയാം. എന്നിട്ടും അവ തമ്മിൽ ബന്ധപ്പെടുന്നില്ലെങ്കിൽ അവ ഡിസ്കണക്ടഡ് ആണെന്ന് പറയുന്നു.
ഇത്തരം ഒരു ലേഖയിലെ എല്ലാ ശീർഷങ്ങളും തമ്മിൽ സ്ട്രോങ്ലി കണക്ടഡ് ആണെങ്കിൽ ആ സദിശലേഖ സ്ട്രോങ്ലി കണക്ടഡ് ആണെന്ന് പറയുന്നു. എല്ലാ ശീർഷങ്ങളും തമ്മിൽ വീക്ലി കണക്ടഡ് മാത്രമാണെങ്കിൽ ആ സദിശലേഖ വീക്ലി കണക്ടഡ് ആണെന്ന് പറയുന്നു. അതിലെ ചില ശീർഷങ്ങൾ ഡിസ്കണക്ടഡ് ആണെങ്കിൽ ആ ലേഖ ഡിസ്കണക്ടഡ് ആണ്.
ബൈപാർട്ടൈറ്റ് ഗ്രാഫ്

ഒരു ലേഖയിലെ ശീർഷങ്ങളുടെ ഗണത്തെ താഴെ പറയുന്ന പ്രകാരം W, X എന്നീ രണ്ടു ഗണങ്ങളായി വിഭജിയ്ക്കാമെങ്കിൽ അതൊരു ബൈപാർട്ടൈറ്റ് ഗ്രാഫ് ആണ്. W ലെ അംഗങ്ങൾ തമ്മിൽ ബന്ധങ്ങൾ ഒന്നും ഉണ്ടാകില്ല, X ലെ അംഗങ്ങൾ തമ്മിലും ബന്ധങ്ങൾ ഒന്നും ഉണ്ടാകില്ല. ഉള്ള ബന്ധങ്ങളെല്ലാം X ലെ ഒരംഗവും W ലെ ഒരംഗവും തമ്മിലായിരിയ്ക്കും.
ഉദാഹരണത്തിന് ഒരു സ്കൂളിലെ അധ്യാപകരും വിദ്യാർത്ഥികളും ശീർഷങ്ങളായുള്ള Z ഒരു ഗണവും w, x നെ പഠിപ്പിയ്ക്കുന്നു എന്ന ബന്ധവും ഉള്ള ലേഖ ഉദാഹരണമായി എടുക്കുക. ഇവിടെ Z എന്ന ഗണത്തെ W എന്ന അധ്യാപകരുടെ ഗണവും X എന്ന വിദ്യാർത്ഥികളുടെ ഗണവുമായും വേർതിരിയ്ക്കാം. W ഗണത്തിലെ അംഗങ്ങൾ തമ്മിൽ ബന്ധം ഒന്നും ഉണ്ടാകില്ല. അതുപോലെ X എന്ന ഗണത്തിലെ അംഗങ്ങളും തമ്മിൽ ബന്ധം ഉണ്ടാകില്ല. ഉള്ള ബന്ധങ്ങളെല്ലാം ഈ രണ്ടു ഗണങ്ങളിലെയും അംഗങ്ങൾ തമ്മിലായിരിയ്ക്കും. അതിനാൽ ഈ ലേഖ ഒരു ബൈപാർട്ടൈറ്റ് ഗ്രാഫിന് ഉദാഹരണമാണ്.
W ഗണത്തിലെ ഓരോ അംഗവും X ഗണത്തിലെ എല്ലാ അംഗങ്ങളുമായും ബന്ധപ്പെട്ടിരിയ്ക്കുന്നുവെങ്കിൽ അതിനെ സമ്പൂർണ ബൈപാർട്ടൈറ്റ് ഗ്രാഫ് എന്നു വിളിയ്ക്കുന്നു. ഒരു ക്ലാസ്സിലെ അധ്യാപകരും കുട്ടികളും തമ്മിലുള്ള ബന്ധം ഉദാഹരണമാണ്. സാധാരണ അവസ്ഥയിൽ ഒരു ക്ലാസ്സിൽ പഠിപ്പിയ്ക്കുന്ന അധ്യാപകരെല്ലാം എല്ലാ കുട്ടികളെയും പഠിപ്പിയ്ക്കും. മറ്റൊരു തരത്തിൽ പറഞ്ഞാൽ ഏതെങ്കിലും കുട്ടിയെ പഠിപ്പിയ്ക്കാത്ത ഒരധ്യാപകനും ഉണ്ടാകില്ല.
പ്ളാനാർ ഗ്രാഫ്
ഒരു ലേഖയിലെ വക്കുകൾ എല്ലാം പരസ്പരം കൂട്ടിമുട്ടാതെ തന്നെ ഒരു പ്രതലത്തിൽ(ഉദാ : ഒരു ഷീറ്റ് പേപ്പറിൽ) വരയ്ക്കാമെങ്കിൽ അതിനെ പ്ളാനാർ ഗ്രാഫ് എന്നു വിളിയ്ക്കാം. ഇങ്ങനെയല്ലാത്ത ഒരു ലേഖയിലെ ചില വക്കുകൾ വരയ്ക്കുമ്പോൾ മറ്റൊരു വക്കിന് കുറുകെ കടന്നുപോകേണ്ടി വരും.
കൊച്ചിയിലെ നാലു സ്ഥലങ്ങൾ തമ്മിൽ റോഡ് മാർഗ്ഗം ബന്ധിപ്പിയ്ക്കുന്ന ഗ്രാഫ് പരിശോധിയ്ക്കുക. ശീർഷങ്ങളുടെ സ്ഥാനം എങ്ങനെയൊക്കെ അഡ്ജസ്റ്റ് ചെയ്ത് വരച്ചാലും വൈറ്റിലയ്ക്കും വരാപ്പുഴയ്ക്കും ഇടയിലുള്ള വക്കും കലൂരിനും കളമശ്ശേരിയ്ക്കും ഇടയിലുള്ള വക്കും പരസ്പരം ക്രോസ്സ് ചെയ്യും. ഇനി കളമശ്ശേരിയെ സൂചിപ്പിയ്ക്കുന്ന ശീർഷം ഈ പ്രതലത്തിൽ എവിടെ വരച്ചാലും ഏതെങ്കിലും രണ്ടു വക്കുകൾ പരസ്പരം ക്രോസ്സ് ചെയ്യും. അതിനാൽ ഈ ലേഖ പ്ലാനാർ ഗ്രാഫ് അല്ല.
സൈക്കിൾ ഗ്രാഫ്
താഴെപ്പറയുന്ന പ്രത്യേകതകൾ ഉള്ള ഒരു ലേഖയാണ് സൈക്കിൾ ഗ്രാഫ്.
- അതിൽ n ≥ 3 ൽ കൂടുതൽ ശീർഷങ്ങൾ ഉണ്ടായിരിയ്ക്കും.
- ഈ ശീർഷങ്ങളെ v1, v2, …, vn എന്ന് നിരത്തി എഴുതാം.
- ഇങ്ങനെ നിരത്തി എഴുതിയാൽ ആ ലേഖയിലെ വക്കുകളെല്ലാം {vi, vi+1} എന്ന ബന്ധം അനുസരിയ്ക്കുന്നു. i = 1, 2, …, n − 1.
- {vn, v1} എന്ന ഒരു വക്കു കൂടി ഇതിൽ ഉണ്ടാവും.
ഇതിലെ എല്ലാ ശീർഷങ്ങളുടെയും ഡിഗ്രി രണ്ട് ആയിരിയ്ക്കും. ഇത് മറ്റൊരു വലിയ ലേഖയുടെ സബ്-ഗ്രാഫ് ആയി വരികയാണെങ്കിൽ വലിയ ഗ്രാഫിൽ ഒരു സൈക്കിൾ അഥവാ സർക്യൂട്ട് ഉണ്ടെന്നു പറയാം.
ട്രീ

കണക്ടഡ് ആയ ഒരു ലേഖയിൽ ഒരൊറ്റ സൈക്കിൾ പോലും ഇല്ലെങ്കിൽ അതിനെ ട്രീ എന്നു വിളിയ്ക്കുന്നു. ഇതിനുള്ള ഏറ്റവും നല്ല ഉദാഹരണമാണ് ഫാമിലി ട്രീ.
ഒരു ലേഖയിൽ ഒരൊറ്റ സൈക്കിൾ പോലും ഇല്ലെങ്കിൽ അതിനെ ഫോറെസ്റ്റ് എന്നു വിളിയ്ക്കുന്നു. അതായത് ഡിസ്കണക്ടഡ് ആയിട്ടുള്ള ഒരു കൂട്ടം ട്രീകളുടെ കൂട്ടമാണ് ഫോറെസ്റ്റ്.
നോട്ടുകൾ
അവലംബം
കൂടുതൽ വായനയ്ക്ക്
പുറംകണ്ണികൾ
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.