Лоренцова сила

Лоренцова сила — комбинација на електрични и магнетни сили на точкест полнеж предизвикани од електромагнетните полиња. Ако честичка со полнеж q се движи со брзина v во присуство на електрично поле E и магнетно поле B, при што на исттот ќе делува сила:

${\displaystyle \mathbf {F} =q\left[\mathbf {E} +(\mathbf {v} \times \mathbf {B} )\right]}$

(во SI единици). Различните записи на оваа основна формула ги опишуваат магнетните сили на жицата преносител на електричната струја (понекогаш наречена Лапласова струја), електромоторната сила во жичена намотка која се движи низ магнетно поле (опфатено со Фарадеевиот закон за индукција), и силата на наелектризирана честичка, која можно е да се движи со брзина блиска до брзината на светлината (релативистички овлик на Лоренцовата сила).

Лоренцовата сила за првпат е математички изведена од страна на Оливер Хевисајд во 1889 година,^[1] иако некои историчари тврдат дека истата се споменува во трудовите на Џејмс Кларк Максвел.^[2] Хендрик Лоренц ја извел неколку години по Хевисајд.

Равенка (SI единици)

Главна статија: Меѓународен систем на мерни единици

Наелектризирана честичка

Лоренцовата сила F на една наелектризирана честичка (со полнеж q) во движење (моментална брзина v). E полето и B поле се менува во просторот и времето.

Силата F дејствува на електричен полнеж q со моментална брзина v, под дејство на надворешно електрично поле E и магнетно поле B, се определува со:^[3]

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$

каде × е векторски производ. Сите задебелени ознаки се вектори. Подетално запишано:

${\displaystyle \mathbf {F} (\mathbf {r} ,\mathbf {\dot {r}} ,t,q)=q[\mathbf {E} (\mathbf {r} ,t)+\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t)]}$

каде r е полупречник-векторот на наелектризираната честичка, t е времето, а точката одозгора е временскиот извод.

Позитивно наелкетризирана честичка ќе биде забрзана во истата линиска насока на E полето, но ќе скршне нормално на векторот на брзината v и B полето во согласност со правилото на десната рака (подетално, ако палецот на десната рака ја покажува брзината v а показалецот магнетното поле B, тогаш средниот прст ја покажува силата F).

Поимот qE се нарекува електрична сила, додека пак поимот qv × B се нарекува магнетна сила.^[4] Според некои дефиниции, поимот „Лоренцова сила“ се однесува специјално на формулата на магнетната сила,^[5] со вкупната електромагнетна сила (вклуќувајќи ја електричната сила) со некои други имиња. Во оваа статија нема да се следи оваа номенклатура: во текстот кој следи поимот „Лоренцова сила“ ќе се однесува само на изразот на вкупната сила.

Компонентата на магнатната сила од Лоренцовата сила се прикажува како силата која дејствува на жицата носител на струјата во магнетното поле. Наречена и Лапласова сила.

Непрекинета распределба на полнежот

Лоренцовата сила (на единица волумен) f при неорекината распределба на полнежот (густината на полнежот ρ) во движење. Густината на струјата J соодествува на движењето на наелектризираниот елемент dq во зафатнинскиот елемент dV и се менува низ континуумот.

За непрекинатата распределба на полнежот во движење, равенката на Лоренцовата сила станува:

${\displaystyle \mathrm {d} \mathbf {F} =\mathrm {d} q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\,\!}$

каде dF е силата на мал дел од распределениот полнеж со набој dq. На двете страни на оваа равенка се поделени со волуменот на малиот дел на распределениот полнеж dV, се добива:

${\displaystyle \mathbf {f} =\rho \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\,\!}$

каде f е густината на силата (сила на единица волумен) и ρ кое е густината на полнежот (полнеж на единица волумен). Понатаму, густината на полнежот е еднаква со движењњето на полнежот во континуумот е:

${\displaystyle \mathbf {J} =\rho \mathbf {v} \,\!}$

па во продолжение аналогот на равенката^[6]

${\displaystyle \mathbf {f} =\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} \,\!}$

Вкупната сила е зафатнински интеграл кој го опфаќа распределениот полнеж:

${\displaystyle \mathbf {F} =\iiint \!(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} )\,\mathrm {d} V.\,\!}$

Со отстранување на ρ и J, користејќи ги Максвеловите равенки, и со употреба на теоремите за векторско сметање, овој облик на равенката може да се искористи за добивање на Максвеловиот тензор σ, пото ова може да се искомбинира со Поинтинговиот вектор S за да се добие електромагнетниот тензор T кој се користи во општата релативност.^[6]

Со други зборови σ и S, друг начин да се запише Лоренцовата сила (на единица волумен) е:^[6]

${\displaystyle \mathbf {f} =\nabla \cdot {\boldsymbol {\sigma }}-{\dfrac {1}{c^{2}}}{\dfrac {\partial \mathbf {S} }{\partial t}}\,\!}$

каде c е брзината на светлината и ∇· ја означува дивергенцијата на тензорското поле. Наместо количеството на полнеж и неговата брзина во електричните и магнетните полиња, оваа равенка се поврзува со енергетскиот флукс (текот на енергија во единица време во единица растојание) во полињата во кои дејствува силата при распределбата на полнежот. Погледајте Коваријантен запис на класичниот електромагнетизам за повеќе детали.

Историја

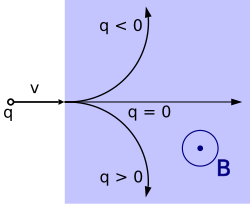
Тректоријта на честичка со позитивен или негативен полнеж q под влијание на магнетното поле B, кое е насочено номално на екранот.

Сноп електрони кои се движат во круг, под дејство на магнетното поле. Се оддава виолетова светлина по должината на патеката на електроните, поради судирите на еклектроните со молекулите на гасот во светликата. Во овој пример се користи телетронска цевка.

Наелектризирани честички под дејство на Лоренцовата сила.

Раните обиди за квантитативно опишување на електромагнетната сила биле спроведени во средината на XVIII век. Било предложено од страна на Јохан Тобијас Мејер и други во 1760 година дека силата на магнетните полови, и електрично наелектризираните објекти, во 1762 година Хенри Кевендиш, забележал дека тие се покоруваат на обратно-квадратниот закон. Сепак, и во двата случаи експерименталниот доказ бил нецелосен ниту пак давал одреден заклучок. Сè до 1784 година ситуацијата не се променила, во таа година Шарл Огистен де Кулон, користејќи усучно нишало, успеал да покаже дека ова било вистина.^[7] Наскоро по ова откритие во 1820 година Ханс Кристијан Ерстед покажал дека на магнетната игла влијае волтаичната струја, Андре-Мари Ампер вомистата година успеал да осмисли преку ексоериментирањето формула за аголната зависност од двете компоненти на електромагнетната сила.^[8][9] Во сите овие записи, силата отсекогаш била определена од условите на својствата на телата и растојанието меѓу истите, отколку од силината на електричното и магнетното поле.^[10]

Современиот концепт на електричното и магнетното поле започнува во теориите на Мајкл Фарадеј, особено неговата идеја за линии на силата, за подоцна истата да добие целосен математички опис од страна на Лорд Келвин и Џејмс Кларк Максвел.^[11] Гледено денес можно да се препознае максвеловиот запис на равенките од 1865 година еден облик на равенката за Лоренцовата сила во однос на електричните струи,^[2] сепак, во времето на Максвел не било очигледно како овие равенки ги поврзуваат силите кај полнежите во движење. Џ.Џ. Томсон бил првиот кој се обидел да ги изведе од Максвеловите равенки за полето, електромагнетните сили кои дејствуваат на наелектризирано тело во движење, т.е својствата на телото и надворешните полиња. Заинтересиран да ги определи електромагнетните својства на наелктризираните честички кај катодните зраци, томсон објавил труд во 1881 година каде тој силата која дејствува на честичките под ејство на надворешно магнетно поле ја пресметал со равенката:^[1]

${\displaystyle \mathbf {F} ={\frac {q}{2}}\mathbf {v} \times \mathbf {B} .}$

Томсон го извел точниот облик на формулата, но, порсди некој помали грешки во пресметките и нецелосниот опис на придвижната струја, вклучил неточен големински фактор од половина пред самата формула. Токму Оливер Хевисајд, кој го има измислено современото векторско запишување и го применил кај Максвеловите равенки за полето, па така во 1885 година и 1889 година ги исправил грешките во томсоновото изведување и дошол до точниот запис на магнетната сила која дејствува на наелектризирано тело во движење.^[1][12][13] Конечно, во 1892 година, Хендрик Лоренц го извел современиот облик на формулата за електромагнетната сила која ги вклучувалча и придонесите на вкупната сила на електричното и магнетното поле. Лоренц започнал да го напушта максвеловите описи на етерот и условите кои владеат во истиот. Наместо тоа, Лоренц направил разлика меѓу материјата и етерот и сакал да ги искористи Максвеловите равенки на микроскопско ниво. Користејќи ја Хевисајдовата верзија на Максвеловите равенки за стационарен етер и употребувајќи ја Лангражовата механика (Погледајте подолу), Лоренц го добил точниот и целосниот облик на законот за силата кој денес го носи неговото име.^[14][15]

Траекториите на честичките под дејство на Лоренцовата сила

Главна статија: Водечки ценатар

Придвижувања на полнежите во хомогено магнетно поле. (A) без присуство на сила (Б) во електрично поле, E (В) во независна сила, F (пример гравитацијата) (Г) во нехомогено магнето поле, како градиент H

Во многу случаи со практична примена, движењето на магнетното поле на електрично наелектризираната честичка (како што е електронот или јонот во плазмата) може да се разгледува како суперпозиција на релативно брзо кружно движење околу точка наречена водечки центар и релативно спорото придвижување на оваа точка. Брзината на придвижувањето може да биде различна за различни видови во зависност од нивната наелектризираност, маса или температура што најверојатно доведува до создавање на електрични струи или хемиски раздвојувања.

Значењето на Лоренцовата сила

Додека современите Максвелови равенки опишуваат како електрично наелектризираните честички и струи или пак подвижните наелектризирани честички создаваат електрични и магнетни полиња, Лоренцовиот закон за силата ја дооформува оваа слика преку опишување на силата која влијае на подвижен точкест полнеж q во присуство на електромагнетни полиња.^[3][16] Лоренцовиот закон за силата го опишува ефектот на E и B на точкест полнеж, но овие електромагнетни сили не ја оформуваат целата слика. Наелектризираните честички можно е да се свзани со други сили, особено гравитациската или пак јадрената сила. Па оттука се заклучува дека Максвеловите равенки, не можат да бидат независни од останатите физички закони, туку станува збор за поврзаност преку полнежот и густините на струите. Реакцијата на точкестиот полнеж на Лоренцовиот закон е еден вид на создавање E и B полиња од страна на струите додека пак создавањето со помош на полнежите е другиот вид на создавање на полињата.

Во материјалите Лоренцовата сила е несоодветна за опишување на однесувањето на наелектризираните честички, како во принцип така и во пресметувањето. Наелектризираните честички во материјалната средина заедно реагираат на E и B полиња и создавањето на овие полиња. Сложените преносни равенки мора да бидат решени за да се определи временското и порсторното дејство на полнежите, на пример, Болцмановата равенка или пак Фокер-Планковата равенка како и Навје-Стоксовите равенки. На пример, Погледајте магнетохидродинамика, динамика на течности, електрохидродинамика, суперпроводливост, ѕвезден развој. Посотои физички апарат за справување со овие проблеми. Погледајте ги на пример, Грин-Кубовите формули и Гриновата функција.

Лоренцовиот закон за силата определен преку E и B

Во многу учебници во кои се разгледува класичниот електромагнетизам, Лоренцовиот закон за силата се користи како дефиниција на електричното и магнетното полев E и B.^[17][18][19] Поточно, Лоренцовата сила се разгледува на начин кој ја следи следнава искуствена изјава:

Електромагнетната сила F на test charge во одредена точа и време е одредена функција од нејзиниот полнеж q и брзината v, која може да се параметризира од точно два вектора E и B, во функционалниот облик:

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$

Ова е точно, во бројните опити кои дури покажале дека истото важи и за честички кои се приближуваар до брзината на светлината (станува збор за, големина на v = |v| = c).^[20] Па така двете векторски полиња E и B се дефинирани низ просторот и времето, и истите се наречени „електрично поле“ и „магнетно поле“. Се забележува дека полињата се дефинирани во времето и просторот во однос на силата која би ја попримил тестирачки полнеж без зависност дали е присутен полнеж на кого би дејствувале силите.

Се забележува дека и кај дефиницијата на E и B, Лоренцовата сила е само дефиниција на начелото бидејќи вистинската честичка (наспроти хипотетичкиот „тестирачки полнеж“ на бесконо малата маса на полнежот) ќе создаде сопствено конечно E и B поле, кои пак ќе ја изменат електромагнетната сила која ја чувствуваат. Во продолжение, доколку полнежот забрзува, како да е присилен да се движи по закривена патека од надворешно дејство, тоа емитува зрачење кое предизвикува iнарушување на сопственото движење. Погледајте на пример закочно зрачење и синхотронска светлина. Овие ефекти се случуваат преку директен ефект (наречен зрачна реактивна сила) и индиректно (преку влијание на движењето на блискиот полнежи и струи). Дополнително, вкупната сила мора да ја вклучува гравитацијата, електрослабото заемодејство, и други сили покрај електромагнетната сила.

Сила во струјо-преносна жица

Магнетно поле на прав спроводник.

Правилото на десната рака за струјо-преносна жица во магнетно поле B

Кога жицата која пренесува електрична струја е сместена во магнетно поле, секој од полнежите во движење, кои ја сочинуваат струјата, се под дејство на Лоренцовата сила, и заедно тие можат се создадат макроскопска сила во жицата (понекогаш наречена Лапласова сила. Со комбинирање на Лоренцовиот закон за силата од погоре со дефинирањето на електричната струја, се добива следната равенка, во случајот на права, неподвижна жица:

${\displaystyle \mathbf {F} =I{\boldsymbol {\ell }}\times \mathbf {B} \,\!}$

каде ℓ е вектор чија големина е должината на жицата, и чија насока е по должината на жицата, подредена со насоката на текот на електричната струја I.

Доколку жицата не е права туку е закривена, силата која дејствува на истата може да се пресмета со применување на формулата за секое бесконечно мало делче на жицата dℓ, па со собирањето на сите овие сили преку интегрирање. Вообичаено, вкупната сила на неподвижна, крута жица која пренесува постојана струја I е

${\displaystyle \mathbf {F} =I\int \mathrm {d} {\boldsymbol {\ell }}\times \mathbf {B} }$

Ова е вкупната сила. Во продолжение, тука сепак ќе постои момент на сила, како и други ефекти доколку жицата не е крута.

Една примена е Амперовата сила, која опишува како две струјо-преносни жици можат да се привлекуваат или одбиваат една од друга, бидејќи секоја ја чувствува Лоренцовата сила од магнетното поле на другата жица. За повеќе информации, Погледајте ја статијата: Амперовата сила.

ЕМС

Магнетната сила (q v × B) компонента на Лоренцовата сила е одговорна за подвижната електромоторна сила (или подвижната ЕМС), појавата која е основата на многуте електрични генератори. Кога проводник се движи низ магнетно поле, магнетната сила се обидува да ги истурка електроните низ жицата, и ова ја создава ЕМС. Поимот „подвижната ЕМС“ е применета кај оваа појава, бидејќи ЕМС настанува под дејство на движењето на жицата.

Во останатите електрични генератори, магнетите се тие кои се движат, додека пак проводниците се неподвижни. Во овој случај, ЕМС настанува под дејство на електричната сила (qE) компонентата од равенката за Лоренцовата сила. Електричното поле се создава поради променливото магнетно поле, што резултира во индуцирана ЕМС, опишана во Максвел–Фарадеевата равенка (едба од четирите современи Максвелови равенки).^[21]

Двете од овие ЕМС, покрај нивните различни начини на настанување, може да се опише со истата равенка, имено, ЕМС е чекорот на промена на магнетниот флукс низ жицата. (Ова е Фарадеевиот закон за индукција, Погледајте погоре.) Ајнштајновата специјална теорија за релативноста била мотивирана од желбата за подобро разбирање на врската меѓу овие два ефекти.^[21] Всушност, електричното и магнетното поле се различни лица на една иста појава, електромагнетното поле, и движејќи се од една инерцијална рамка во друга, солеидното векторско поле како дел од E-поле, може во целина или делумно да премине во B-поле или обратно.^[22]

Лоренцовата сила и Фарадеевиот закон за индукција

Главна статија: Фарадеев закон за индукција

Имајќи намотка на жица во магнетно поле, Фарадеевиот закон за индукција гласи дека индуцираната електромоторна сила (ЕМС) во жицата изнесува:

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}}$

каде

${\displaystyle \Phi _{B}=\iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot \mathbf {B} (\mathbf {r} ,t)}$

е магнетниот флукс низ намотката, B е магнетното поле, Σ(t) е површината образована од затворената контура ∂Σ(t), при време t, dA е бесконечно малиот векторски елемент на Σ(t) (величината е површината на бесконечномалиот дел од површината, насоката е нормална на тој дел од површината).

Знакот на ЕМС е определен од Ленцовиот закон. Се зема предвид дека ова важи не само за неподвижна жица — туку и за подвижна жица.

Од Фарадеевиот закон за индукција (важи за подвижна жица, на пример во моторите) и Максвеловите равенки, може да се изведе Лоренцовата сила. Важи и обратното, Лоренцовата сила и Максвеловите равенки можат да се употребат за иведување на Фарадеевиот закон.

Нека Σ(t) е подвижната жица, движејќи се без вртење и со постојана брзина v и Σ(t) е внатрешната површина на жицата. ЕМС околу затворена контура ∂Σ(t) е определена со:^[23]

${\displaystyle {\mathcal {E}}=\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q}$

каде

${\displaystyle \mathbf {E} =\mathbf {F} /q}$

е електричното поле и dℓ е бесконечно малиот векторски елемент на контирата ∂Σ(t).

Патем: dℓ и dA имаат променлив знак, за да се определи точниот знак, се користи правилото на десната рака, како што е објаснето во статијата за Келвин-Стоксовата теорема.

Горниот резултат може да се спореди со верзијата на Фарадеевиот закон за индукција кој се појавува во современите Максвелови равенки, кои во статијата се наречени Максвел-Фарадеева равенка:

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\ .}$

Максвел-Фарадеевата равенка може да биде запишана и во интегрален облик користејќи ја Келвин-Стоксовата теорема:.^[24]

Па така се добива, Максвел-Фарадеевата равенка:

${\displaystyle \oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {E} (\mathbf {r} ,\ t)=-\ \iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot {{\mathrm {d} \,\mathbf {B} (\mathbf {r} ,\ t)} \over \mathrm {d} t}}$

и Фарадеевиот закон,

${\displaystyle \oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q(\mathbf {r} ,\ t)=-{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot \mathbf {B} (\mathbf {r} ,\ t).}$

Двете се еквивалентни доколку станува збор за неподвижна жица. Употребувајќи го Лајбницовото интегрално правило и дека div B = 0, се добива,

${\displaystyle \oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q(\mathbf {r} ,t)=-\iint _{\Sigma (t)}\mathrm {d} \mathbf {A} \cdot {\frac {\partial }{\partial t}}\mathbf {B} (\mathbf {r} ,t)+\oint _{\partial \Sigma (t)}\!\!\!\!\mathbf {v} \times \mathbf {B} \,\mathrm {d} {\boldsymbol {\ell }}}$

и кортистејќи ја Максвел-Фарадеевата равенка,

${\displaystyle \oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {F} /q(\mathbf {r} ,\ t)=\oint _{\partial \Sigma (t)}\mathrm {d} {\boldsymbol {\ell }}\cdot \mathbf {E} (\mathbf {r} ,\ t)+\oint _{\partial \Sigma (t)}\!\!\!\!\mathbf {v} \times \mathbf {B} (\mathbf {r} ,\ t)\,\mathrm {d} {\boldsymbol {\ell }}}$

бидејќи ова важи за која и да е местоположба на жицата важи,

${\displaystyle \mathbf {F} =q\,\mathbf {E} (\mathbf {r} ,\ t)+q\,\mathbf {v} \times \mathbf {B} (\mathbf {r} ,\ t).}$

Фарадеевиот закон за индукција важи без разлика дали намотката на жицата е крута и неподвижна, или е во движење и притоа се деформира, и важи без разлика дали магнетното поле е постојано или пак се менува со текот на времето. Сепак, постојат случаи каде Фарадеевиот заккон е несоодветен или пак тежок за употреба, па потребно е да се искорити Лоренцовиот закон за силата. Погледајте неприменливост на Фарадеевиот закон.

Доколку магнетното поле е сврзано со времето и проводната намотка се движи низ полето, магнетниот флукс Φ_B кој е поврзан со намотката може да се промени на неколку начини. На пример, ако B - полето се менува со местоположбата, и ако намотката се движи кон местоположба со друго B- поле, Φ_B се менува. Со други зборови, доколку намотката ја смени насоката во однос на B - поле, B • dA диференцијалниот елеменент ќе се промени поради различниот агол меѓу B и dA, со што се менува и Φ_B. Како трет пример, Ако дел од колото се протне низа истородно, временски независно B- поле, и другиот дел од колото е неподвижен, флуксот кој го поврзува целото коло може да се промени поради промената на релативната местоположба на колото со текот на времето (површината ∂Σ(t) е временски зависна). Во сите три случаи, Фарадеевиот закон за индукција ја предвидува ЕМС создадена од промената на Φ_B.

Се забележува дека Максвел-Фарадееват равенка тврди дека електричното поле E не се запазува кога амгнетното поле B се менува со текот на времето, и не може да се изрази како градиентот на скаларното поле, и не е под дејство на градиентната теорема бидејќи сопствениот ротор не е нула.Погледајте.^[23][25]

Лоренцовата сила изразена преку потенцијалите

Главни статии: Математички описи на електромагнетното поле, Максвелови равенки, и Хелмхолцова теорема

E и B полињата можат да се заменат со магнетниот векторски потенцијал A и (скаларниот) електростатички потенцијал ϕ од

${\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}$

${\displaystyle \mathbf {B} =\nabla \times \mathbf {A} }$

каде ∇ е симбол за градиент, ∇• е дивергенција, ∇ × е ротор.

Па силата станува

${\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )\right]}$

и користејќи го идентитетот за тројниот произод се упростува на

${\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\nabla (\mathbf {v} \cdot \mathbf {A} )-(\mathbf {v} \cdot \nabla )\mathbf {A} \right]}$

користејќи го изводот на сложената функција, вкупниот извод од A е:

${\displaystyle {\frac {\mathrm {d} \mathbf {A} }{\mathrm {d} t}}={\frac {\partial \mathbf {A} }{\partial t}}+(\mathbf {v} \cdot \nabla )\mathbf {A} }$

па така горниот израз може да се презапише на следниот начин;

${\displaystyle \mathbf {F} =q\left[-\nabla (\phi -\mathbf {v} \cdot \mathbf {A} )-{\frac {d\mathbf {A} }{\mathrm {d} t}}\right]}$

која пак може да биде запишана со пригодниот Ојлер-Лангранжов облик

${\displaystyle \mathbf {F} =q\left[-\nabla _{\mathbf {x} }(\phi -{\dot {\mathbf {x} }}\cdot \mathbf {A} )+{\frac {\mathrm {d} }{\mathrm {d} t}}\nabla _{\dot {\mathbf {x} }}(\phi -{\dot {\mathbf {x} }}\cdot \mathbf {A} )\right]}$

Лоренцовата сила и аналитичката механика

Поврзано: Импулс

Лагранжијанот за наелектризирана честичка со маса m и полнеж q во електромагнетно поле еквивелаентно ка опишува динамиката на честичката во зависност од нејзината енергија, отколку од силата која дејствува на истата. Класичниот израз е даден со:^[26]

${\displaystyle L={\frac {m}{2}}\mathbf {\dot {r}} \cdot \mathbf {\dot {r}} +q\mathbf {A} \cdot \mathbf {\dot {r}} -q\phi }$

каде A и ϕ се потенцијалните полиња од погоре. Користејќи Ланранжови равенки, може да се добие равенката за Лоренцоватѕа сила.

Изведување на Лоренцовата сила од класичниот Лагранжијан (SI единици)

За A полето, честичка која се движи со брзина v = ṙ има импулс ${\displaystyle q\mathbf {A} (\mathbf {r} ,t)}$, па неговата потенцијална енергија е ${\displaystyle q\mathbf {A} (\mathbf {r} ,t)\cdot \mathbf {\dot {r}} }$. За ϕ поле, потенцијалната енергија на честичката е ${\displaystyle q\phi (\mathbf {r} ,t)}$. Вкупната потенцијална енергија тогаш е: ${\displaystyle V=q\phi -q\mathbf {A} \cdot \mathbf {\dot {r}} }$ а кинетичката енергија е: ${\displaystyle T={\frac {m}{2}}\mathbf {\dot {r}} \cdot \mathbf {\dot {r}} }$ па оттука Лангражијанот: ${\displaystyle L=T-V={\frac {m}{2}}\mathbf {\dot {r}} \cdot \mathbf {\dot {r}} +q\mathbf {A} \cdot \mathbf {\dot {r}} -q\phi }$ ${\displaystyle L={\frac {m}{2}}({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})+q({\dot {x}}A_{x}+{\dot {y}}A_{y}+{\dot {z}}A_{z})-q\phi }$ Лангранжовите равенки се ${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {x}}}}={\frac {\partial L}{\partial x}}}$ (исто и за y и z). По пресметуивањето на парцијалните изводи: ${\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {x}}}}&=m{\ddot {x}}+q{\frac {\mathrm {d} A_{x}}{\mathrm {d} t}}\\&=m{\ddot {x}}+{\frac {q}{\mathrm {d} t}}\left({\frac {\partial A_{x}}{\partial t}}dt+{\frac {\partial A_{x}}{\partial x}}dx+{\frac {\partial A_{x}}{\partial y}}dy+{\frac {\partial A_{x}}{\partial z}}dz\right)\\&=m{\ddot {x}}+q\left({\frac {\partial A_{x}}{\partial t}}+{\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{x}}{\partial y}}{\dot {y}}+{\frac {\partial A_{x}}{\partial z}}{\dot {z}}\right)\\\end{aligned}}}$ ${\displaystyle {\frac {\partial L}{\partial x}}=-q{\frac {\partial \phi }{\partial x}}+q\left({\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{y}}{\partial x}}{\dot {y}}+{\frac {\partial A_{z}}{\partial x}}{\dot {z}}\right)}$ изедначувајќи и упростувајќи се добива: ${\displaystyle m{\ddot {x}}+q\left({\frac {\partial A_{x}}{\partial t}}+{\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{x}}{\partial y}}{\dot {y}}+{\frac {\partial A_{x}}{\partial z}}{\dot {z}}\right)=-q{\frac {\partial \phi }{\partial x}}+q\left({\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{\frac {\partial A_{y}}{\partial x}}{\dot {y}}+{\frac {\partial A_{z}}{\partial x}}{\dot {z}}\right)}$ ${\displaystyle {\begin{aligned}F_{x}&=-q\left({\frac {\partial \phi }{\partial x}}+{\frac {\partial A_{x}}{\partial t}}\right)+q\left[{\dot {y}}\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)+{\dot {z}}\left({\frac {\partial A_{z}}{\partial x}}-{\frac {\partial A_{x}}{\partial z}}\right)\right]\\&=qE_{x}+q[{\dot {y}}(\nabla \times \mathbf {A} )_{z}-{\dot {z}}(\nabla \times \mathbf {A} )_{y}]\\&=qE_{x}+q[\mathbf {\dot {r}} \times (\nabla \times \mathbf {A} )]_{x}\\&=qE_{x}+q(\mathbf {\dot {r}} \times \mathbf {B} )_{x}\end{aligned}}}$ слично и за насоките y и z. Па оттука равенката за силата е: ${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {\dot {r}} \times \mathbf {B} )}$

Потенцијалната енергија зависи од брзината на честичката, па честичката е зависна од брзината, па следи дека истата не е запазувачка.

Релативистичкиот Лангранжијан е

${\displaystyle L=-mc^{2}{\sqrt {1-\left({\frac {\dot {\mathbf {r} }}{c}}\right)^{2}}}+e\mathbf {A} (\mathbf {r} )\cdot {\dot {\mathbf {r} }}-e\phi (\mathbf {r} )\,\!}$

Дејството е релативстичката лачна должина на патеката на честичката во време-просторот, минус придонесот на потенцијалната енергија, плус дополнителен придонес кој е квантно механички дополнителна фаза која наелектризираната честичка ја стекнува кога се движи надолж векторскиот потенцијал.

Изведување на Лоренцовата сила од релативистичкиот Лангранжијан (SI единици)

Равенките на честичката во движење се изведени со доведување во крајност на дејството (Погледајте матрично сметање): ${\displaystyle {\frac {\mathrm {d} \mathbf {P} }{\mathrm {d} t}}={\frac {\partial L}{\partial \mathbf {r} }}=e{\partial \mathbf {A} \over \partial \mathbf {r} }\cdot {\dot {\mathbf {r} }}-e{\partial \phi \over \partial \mathbf {r} }\,\!}$ ${\displaystyle \mathbf {P} -e\mathbf {A} ={\frac {m{\dot {\mathbf {r} }}}{\sqrt {1-\left({\frac {\dot {\mathbf {r} }}{c}}\right)^{2}}}}\,}$ се исти како и Хамилтоновите равенки за движење: ${\displaystyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\frac {\partial }{\partial \mathbf {p} }}\left({\sqrt {(\mathbf {P} -e\mathbf {A} )^{2}+(mc^{2})^{2}}}+e\phi \right)\,\!}$ ${\displaystyle {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}=-{\partial \over \partial \mathbf {r} }\left({\sqrt {(\mathbf {P} -e\mathbf {A} )^{2}+(mc^{2})^{2}}}+e\phi \right)\,\!}$ двете се еквивалентни на неканонските облици: ${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({m{\dot {\mathbf {r} }} \over {\sqrt {1-\left({\frac {\dot {\mathbf {r} }}{c}}\right)^{2}}}}\right)=e\left(\mathbf {E} +{\dot {\mathbf {r} }}\times \mathbf {B} \right).\,\!}$ Оваа равенка е Лоренцовата сила, претставувајќи го чекорот со кој ЕМ поле додава релативистички импулс на честичката.

Равенка (cgs единици)

Поврзано: cgs единици

Горе споменатата равенка е за SI единици кои најчесто се користат меѓу експерименталистите, техничарите и инженерите. Во cgs-Гаусови единици, кои поретко се користат меѓу теоретските физичари, се добива

${\displaystyle \mathbf {F} =q_{\mathrm {cgs} }\left(\mathbf {E} _{\mathrm {cgs} }+{\frac {\mathbf {v} }{c}}\times \mathbf {B} _{\mathrm {cgs} }\right).}$

каде c е брзината на светлината. Иако ова равенка изгледа малку поинаку, целосно е еквивалентна, бидејќи важат следниве релации:

${\displaystyle q_{\mathrm {cgs} }={\frac {q_{\mathrm {SI} }}{\sqrt {4\pi \epsilon _{0}}}},\quad \mathbf {E} _{\mathrm {cgs} }={\sqrt {4\pi \epsilon _{0}}}\,\mathbf {E} _{\mathrm {SI} },\quad \mathbf {B} _{\mathrm {cgs} }={\sqrt {4\pi /\mu _{0}}}\,{\mathbf {B} _{\mathrm {SI} }}}$

каде ε₀ е електричната константа и μ₀ е магнетната константа. Во практиката, подзаписот „cgs“ и „SI“ се секогаш изоставени, користениот систем на единици треба самостојно да се процени од самиот запис.

Релативистички облик на Лоренцовата сила

Коваријантен облик на Лоренцовата сила

Тензор на полето

Главни статии: Коваријантен запис на класичниот електромагнетизам и Математички описи на електромагнетната сила

Користејќи го метричкиот запис (-1, 1, 1, 1), Лоренцовата сила за полнежот q може да се запише во коваријантен облик:

${\displaystyle {\frac {\mathrm {d} p^{\alpha }}{\mathrm {d} \tau }}=qU_{\beta }F^{\alpha \beta }}$

каде p^α е четири-импулсот, дефиниран како

${\displaystyle p^{\alpha }=\left(p_{0},p_{1},p_{2},p_{3}\right)=\left(\gamma mc,p_{x},p_{y},p_{z}\right)\,,}$

τ е сопственото време на честичката, F^αβ е коваријантниот електромагнетен тензор

${\displaystyle F^{\alpha \beta }={\begin{pmatrix}0&E_{x}/c&E_{y}/c&E_{z}/c\\-E_{x}/c&0&B_{z}&-B_{y}\\-E_{y}/c&-B_{z}&0&B_{x}\\-E_{z}/c&B_{y}&-B_{x}&0\end{pmatrix}}}$

и U е коваријантната 4-брзината на честичката, определена со:

${\displaystyle U_{\beta }=\left(U_{0},U_{1},U_{2},U_{3}\right)=\gamma \left(-c,v_{x},v_{y},v_{z}\right)\,,}$

во која

${\displaystyle \gamma (v)={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-{\frac {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}{c^{2}}}}}}}$

е Лоренцовиот фактор.

Полињата се трансформираат во рамка која се движи со постојана релативна брзина:

${\displaystyle F'^{\mu \nu }={\Lambda ^{\mu }}_{\alpha }{\Lambda ^{\nu }}_{\beta }F^{\alpha \beta }\,,}$

каде Λ^μ_α е тензорот на Лоренцовата преобразба.

Транслација во векторски запис

Компонентата α = 1 (x- компонентата) на силата е

${\displaystyle {\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=qU_{\beta }F^{1\beta }=q\left(U_{0}F^{10}+U_{1}F^{11}+U_{2}F^{12}+U_{3}F^{13}\right).\,}$

Заменувајќи ги компонентите на коваријантниот електромагнетен тензор F дава

${\displaystyle {\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=q\left[U_{0}\left({\frac {-E_{x}}{c}}\right)+U_{2}(B_{z})+U_{3}(-B_{y})\right].\,}$

Користејќи ги компонентите на коваријантната четири-брзина се добива

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}&=q\gamma \left[-c\left({\frac {-E_{x}}{c}}\right)+v_{y}B_{z}+v_{z}(-B_{y})\right]\\&=q\gamma \left(E_{x}+v_{y}B_{z}-v_{z}B_{y}\right)\\&=q\gamma \left[E_{x}+\left(\mathbf {v} \times \mathbf {B} \right)_{x}\right]\,.\end{aligned}}}$

Преаметката за α = 2, 3 (компонентите на силата во насоките y и z) дава слични резултати, па собирајќи ги овие 3 равенки во една:

${\displaystyle {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} \tau }}=q\gamma \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\,,}$

и бидејќи изводите во временските координати dt и сопственото време dτ се поврзани со Лоренцовиот фактор,

${\displaystyle dt=\gamma (v)d\tau \,,}$

па се добива

${\displaystyle {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}=q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\,.}$

Ова е токму бараниот Лоренцов закон за силата, сепак, важно е да се забележи дека p е релативистичкиот израз,

${\displaystyle \mathbf {p} =\gamma (v)m_{0}\mathbf {v} \,.}$

Временско-просторно алгебарски облик на Лоренцовата сила

Електричното и магнетното поле се зависни од брзината на набљудувачот, па релативистичкиот облик на Лоренцовиот закон за силата може најдобро да образло9жи почнувајќи од координатно независен израз за електромагнетните и магнетните полиња,^[27] ${\displaystyle {\mathcal {F}}}$, и произволната временска насока, ${\displaystyle \gamma _{0}}$, каде

${\displaystyle \mathbf {E} =({\mathcal {F}}\cdot \gamma _{0})\gamma _{0}}$

и

${\displaystyle i\mathbf {B} =({\mathcal {F}}\wedge \gamma _{0})\gamma _{0}}$

${\displaystyle {\mathcal {F}}}$ е време-просторниот бивектор (насочен површински отсечок, како што векторот е насочен дел од правата), кој има шест степени на слобода кој соодејствуваат на изблици (вртежи во време-просторните рамнини) и вртежи. Точкестиот производ со векторот ${\displaystyle \gamma _{0}}$ извлекува вектор од транслациониот дел, додека пак клинестиот производ создава тривектор које двојник на векторто кој е вообичаениот вектор на магнетното поле. Релативистичката брзина се менува со временската местоположба на векторот ${\displaystyle v={\dot {x}}}$, каде

${\displaystyle v^{2}=1,}$

и брзината е

${\displaystyle \mathbf {v} =cv\wedge \gamma _{0}/(v\cdot \gamma _{0}).}$

Соодветниот облик на Лоренцовиот закон за силата е едноставно

${\displaystyle F=q{\mathcal {F}}\cdot v}$

Се забележува дека редоследот е важен меѓу бивекторот и векторот на точкестиот прроизвод е антисиметричен. Од временско-просторното раздвојување може да се добие брзината, и полињата од погоре го даваат вообичаениот израз.

Примена

Лоренцова сила со осцилоскоп.

Лоренцовата сила се јавува кај многу апарати, вклучувајќи ги и:

• Циклотроните
• Масен спектрометар
• Брзински филтри
• Магнетроните
• Лоренцово силни брзиномери

Појавувајќи се како Лапласова сила на електричната струја во проводникот, оваа сила се случува во многум апарати како што се:

Електричен мотор Шински топ Линиски мотор Звучник

Магнето-плазмичнодинамичен мотор Електричен генератор Истополен генератор Линиски алтернатор

Поврзано

Холов ефект Електромагнетизам Гравитомагнетизам Амперов закон за силата Хендрик Лоренц Максвелови равенки Запишување на Mаксвеловите равенки во специјалата релативност

Подвижен магнет и проводнички проблем Абрахам–Лоренцова сила Ларморова равенка Циклотронско зрачење Магнетен потенцијал Магнетоотпор

Скаларен потенцијал Хелмхолцова теорема Водечки центар Линија на полето

„Лоренцова сила“ на Ризницата ?

Наводи

1. Oliver Heaviside By Paul J. Nahin, p120
2. Huray, Paul G. (2009). Maxwell's Equations. Wiley-IEEE. стр. 22. ISBN 0-470-54276-4.
3. See Jackson page 2. The book lists the four modern Maxwell's equations, and then states, "Also essential for consideration of charged particle motion is the Lorentz force equation, F = q ( E+ v × B ), which gives the force acting on a point charge q in the presence of electromagnetic fields."
4. See Griffiths page 204.
5. For example, see the website of the "Lorentz Institute": \, or Griffiths.
6. Griffiths, David J. (1999). Introduction to electrodynamics. reprint. with corr. (3. изд.). Upper Saddle River, New Jersey [u.a.]: Prentice Hall. ISBN 978-0-13-805326-0.
7. Meyer, Herbert W. (1972). A History of Electricity and Magnetism. Norwalk, Connecticut: Burndy Library. стр. 30–31. ISBN 0-262-13070-X.
8. Verschuur, Gerrit L. (1993). Hidden Attraction : The History And Mystery Of Magnetism. New York: Oxford University Press. стр. 78–79. ISBN 0-19-506488-7.
9. Darrigol, Olivier (2000). Electrodynamics from André Ampère to Albert Einstein. Oxford, [England]: Oxford University Press. стр. 9, 25. ISBN 0-19-850593-0.
10. Verschuur, Gerrit L. (1993). Hidden Attraction : The History And Mystery Of Magnetism. New York: Oxford University Press. стр. 76. ISBN 0-19-506488-7.
11. Darrigol, Olivier (2000). Electrodynamics from André Ampère to Albert Einstein. Oxford, [England]: Oxford University Press. стр. 126–131, 139–144. ISBN 0-19-850593-0.
12. Darrigol, Olivier (2000). Electrodynamics from André Ampère to Albert Einstein. Oxford, [England]: Oxford University Press. стр. 200, 429–430. ISBN 0-19-850593-0.
13. Heaviside, Oliver. "On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric".
14. Darrigol, Olivier (2000). Electrodynamics from André Ampère to Albert Einstein. Oxford, [England]: Oxford University Press. стр. 327. ISBN 0-19-850593-0.
15. Whittaker, E. T. (1910). A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century. Longmans, Green and Co. стр. 420–423. ISBN 1-143-01208-9.
16. See Griffiths page 326, which states that Maxwell's equations, "together with the [Lorentz] force law...summarize the entire theoretical content of classical electrodynamics".
17. See, for example, Jackson p777-8.
18. J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. стр. 72–73. ISBN 0-7167-0344-0.CS1-одржување: повеќе имиња: список на автори (link). These authors use the Lorentz force in tensor form as definer of the electromagnetic tensor F, in turn the fields E and B.
19. I.S. Grant, W.R. Phillips, Manchester Physics (2008). Electromagnetism (2. изд.). John Wiley & Sons. стр. 122. ISBN 978-0-471-92712-9.CS1-одржување: повеќе имиња: список на автори (link)
20. I.S. Grant, W.R. Phillips, Manchester Physics (2008). Electromagnetism (2nd Edition). John Wiley & Sons. стр. 123. ISBN 978-0-471-92712-9.CS1-одржување: повеќе имиња: список на автори (link)
21. See Griffiths pages 301–3.
22. Tai L. Chow (2006). Electromagnetic theory. Sudbury MA: Jones and Bartlett. стр. 395. ISBN 0-7637-3827-1.
23. Landau, L. D., Lifshit︠s︡, E. M., & Pitaevskiĭ, L. P. (1984). Electrodynamics of continuous media; Volume 8 Course of Theoretical Physics (Second. изд.). Oxford: Butterworth-Heinemann. стр. §63 (§49 pp. 205–207 in 1960 edition). ISBN 0-7506-2634-8.CS1-одржување: повеќе имиња: список на автори (link)
24. Roger F Harrington (2003). Introduction to electromagnetic engineering. Mineola, New York: Dover Publications. стр. 56. ISBN 0-486-43241-6.
25. M N O Sadiku (2007). Elements of elctromagnetics (Fourth. изд.). NY/Oxford: Oxford University Press. стр. 391. ISBN 0-19-530048-3.
26. Classical Mechanics (2nd Edition), T.W.B. Kibble, European Physics Series, Mc Graw Hill (UK), 1973, ISBN 0-07-084018-0.
27. Hestenes, David. „SpaceTime Calculus“. Архивирано од изворникот на 2021-05-09. Посетено на 2015-05-03.

Надворешни врски

• Interactive Java tutorial on the Lorentz force National High Magnetic Field Laboratory
• Faraday's law: Tankersley and Mosca Архивирано на 26 февруари 2009 г.
• Notes from Physics and Astronomy HyperPhysics at Georgia State University; see also home page
• Interactive Java applet on the magnetic deflection of a particle beam in a homogeneous magnetic field Архивирано на 13 август 2011 г. by Wolfgang Bauer