Plokščia banga
From Wikipedia, the free encyclopedia
Remove ads
Plokščioji banga – bangų fizikos sąvoka, reiškianti pastovaus dažnio bangą, kurios bangos frontai (vienodos fazės paviršiai) yra begalinės lygiagrečios plokštumos, statmenos sklidimo (fazinio greičio vektoriaus) krypčiai.
| |
Šiam straipsniui ar jo daliai trūksta išnašų į patikimus šaltinius. Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais. |
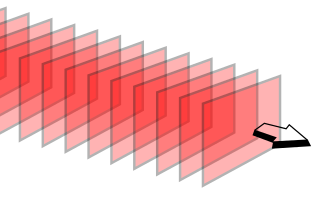

Šis terminas taip pat yra vartotinas aprašant tas bangas, kurios yra apytiksliai plokščios nagrinėjamoje erdvės srityje. Pavyzdžiui, tokio riboto šaltinio, kaip antena kuriamas laukas yra apytiksliai plokščia banga savo tolimajame lauke. Būtina paminėti, kad optinis "spindulys", geometrinės optikos artinyje (sklidimas vienalytėje terpėje atstumais žymiai didesniais negu bangos ilgis) apytiksliai atitinka lokaliame taške plokščią bangą, kurios bangos vektorius sutampa su spindulio kryptimi.
Plokščioji banga yra bangų lygties sprendinys užrašomas tokiame pavidale:
kur i yra menamas vienetas, k yra bangos vektorius, ω yra kampinis dažnis, o a yra kompleksinė amplitudė. Fizikinis dydis atitinka realiąją šios išraiškos dalį.
Ši išraiška yra skaliarinės bangų lygties vienalytėje terpėje sprendinys. Vektorinės bangų lygtys, aprašančios, pvz., elektromagnetinės bangas arba bangas tampriame kūne, turi panašios išraiškos sprendinį: , kur pastovus vektorius yra bangos amplitudė. Pavyzdžiui, elektromagnetizme dažniausiai yra vektorius, aprašantis elektrinį lauką, magnetinį lauką arba vektorinį potencialą. Skersinė banga yra tokia banga, kurioje amplitudės vektorius yra statmenas k (pvz., elektromagnetinės bangos izotropinėje terpėje), tuo tarpu išilginė banga yra ta, kurioje amplitudės vektorius yra lygiagretus k (pvz., akustinės bangos skystyje arba dujose).
Aukštesnėje lygtyje, funkcija ω(k) apibrėžia terpės dispersinį sąryšį. Santykis ω/|k| apibrėžia plokščios bangos fazinio greičio dydį, o dydis dω/dk - grupinį greitį.
Remove ads
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



