Triangolo

Un triangolo o l'é un poligono con trei loei e træ ponte (ò pissi). A l'é uña de forme de base da geometria. Un triangolo con ponte ${\displaystyle A}$, ${\displaystyle B}$ e ${\displaystyle C}$ o s'indica con ${\displaystyle \triangle ABC}$.

ZE	Sta pagina a l'é scrita in zeneise, segondo a grafia unitäia

Inta geometria euclidea, tutte e combinaçioin de trei ponti che no seggian conlineæ determinan un triangolo unico e, a-o mæximo tempo, un cian unico (saieiva à dî un spaçio euclideo à doe dimençioin). In atre poule, gh'é un solo cian ch'o contëgne quello triangolo, e ògni triangolo o l'é contegnuo inte un dæto cian.

Se o spaçio consciderou o l'é o cian euclideo, aloa gh'é un solo cian e tutti i triangoli ghe stan drento. Pe contra, inti spaçi euclidei de dimenscion maggiô, sto fæto o no l'é ciù veo. St'articolo o tratta di triangoli inta geometria euclidea.

Clascificaçion di triangoli

I triangoli se peuan clascificâ da-a longhixe relativa di seu loei, ò da-a grandessa relativa di seu angoli:

• O triangolo equilatero o l'à tutti i loei da mæxima longhixe ò, de mainea equivalente, tutti i angoli da mæxima grandessa.
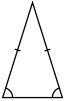
• O triangolo isòscele o l'à doî di loei da mæxima longhixe, ò doi di angoli da mæxima grandessa, ch'o l'é equivalente.
• O triangolo scalen o l'à tutti i loei e tutti i angoli despægi.

Equilatero	Isòscele	Scalen

Differente, se peu ascì clascificâ i triangoli da-a grandessa do seu angolo ciù grande:

• O triangolo rettangolo ò drito o l'à un di angoli da 90°, saieiva à dî un angolo drito. O lou ch’o s’attreuva in diagonâ respetto à l’angolo o l'é dito ipotenusa, e o l'é o ciù longo. I atri doî loei en ciammæ cateti. O l'é o triangolo pe-o quæ o vâ o teorema de Pitagora.
• O triangolo ottusangolo ò ottuso o l'à un angolo de ciù de 90°, saieiva à dî un angolo ottuso.
• O triangolo acutangolo ò agusso o l'à tutti trei i angoli de grandessa minô de 90°, saieiva à dî di angoli agussi.

Drito	Ottuso	Agusso

Pe de ciù, un triangolo o l'é dito degenerou quande o l'à un angolo de 180°, ò sæ un angolo cian.

Condiçioin d'existensa

Dæto træ longhixe, segondo a disegualiansa triangolâ, un triangolo con i loei de ste longhixe o peu existe solo se respettan a disegualiansa. Pe-i triangoli degeneræ, donde e trei ponte en conlineæ e forman un segmento, a disegualiansa a vëgne unn'egualiansa.

Dæto trei angoli, questi peuan formâ un triangolo solo se en de grandessa maggiô ò pægia à zero, e se a seu somma a l'é pægia à 180°. Se s'ammette di angoli de 0°, o triangolo ch'o ne sciòrte o l'é degenerou.

Atri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons a contêgne di files in sce Trangolo

Contròllo de outoritæ	LCCN (EN) sh85137407 · BNF (FR) cb11946969k (data)