복소평면

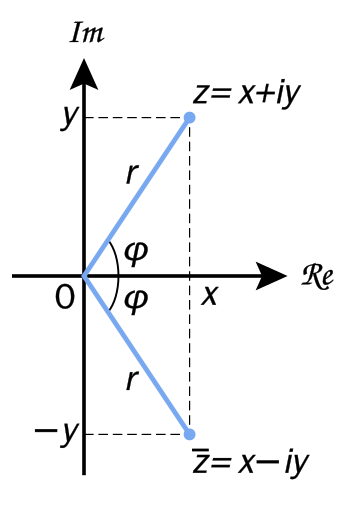
수학에서, 복소평면(複素平面)은 복소수를 기하학적으로 표현하기 위해 개발된 좌표평면으로 서로 직교하는 실수축과 허수축으로 이루어져 있다. 이것은 복소수의 실수부가 실수축에, 허수부가 허수축에 대응된 형태의 데카르트 좌표로 볼 수 있다.

복소평면에 나타낸 복소수 z와 켤레복소수의 기하학적 표현. 원점에서 점 z를 따라 그어진 파란색 선의 거리는 복소수 z의 절댓값을 나타내고 각 ¢은 z의 논의를 나타낸다.

복소평면의 개념은 복소수의 기하학적 해석을 가능하게 한다. 덧셈연산 하에서, 복소수들은 복소평면상에서 벡터처럼 더해진다. 두 복소수의 곱셈은 극좌표를 이용하면 쉽게 표현할 수 있다. 특히 복소수의 크기가 1인 복소수 간의 곱셈은 회전하는 것처럼 행동한다. 삼각함수의 덧셈정리에 의하여, ${\displaystyle (\cos A+i\sin A)(\cos B+i\sin B)=(\cos A\cos B-\sin A\sin B)+i(\sin A\cos B+\cos A\sin B)=\cos(A+B)+i\sin(A+B)}$가 되어 회전한 결과와 같게 된다.

정의

복소수는 다음과 같이 정의하는 수이다.

${\displaystyle z=\mathrm {Re} z+i\mathrm {Im} z}$ (${\displaystyle \mathrm {Re} z}$, ${\displaystyle \mathrm {Im} z}$는 실수, ${\displaystyle i={\sqrt {-1}}}$)

다시 말해, 하나의 복소수는 실수 두개로 이뤄진 하나의 순서쌍과 대응시킬 수 있다. 하나의 순서쌍은 좌표평면의 한 점으로 대응되기 때문에 복소수 역시 좌표평면상의 한 점으로 나타낼 수 있다. 일반적으로 실수부는 ${\displaystyle x}$좌표로, 허수부는 ${\displaystyle y}$좌표로 대응시킨다.

${\displaystyle z(x,y)=x+iy}$

극좌표를 이용하여 ${\displaystyle z=x+iy}$ 를

${\displaystyle z=r(\cos \theta +i\sin \theta )}$

라고 표현하며, 이 경우, 실수부와 허수부는 각각,

${\displaystyle x=r\cos \theta }$

${\displaystyle y=r\sin \theta }$

이다. 또한, 오일러의 공식을 이용하여

${\displaystyle z=re^{i\theta }}$

라고 쓴다.

원점과 점${\displaystyle z}$를 이은 직선과 실수축 사이의 각인 ${\displaystyle \theta }$는 ${\displaystyle z}$의 편각이라고 하며, 삼각함수는 주기가 ${\displaystyle 2\pi }$이기 때문에 ${\displaystyle z}$의 편각이 ${\displaystyle \theta }$ 일때, ${\displaystyle \theta +2n\pi }$ (${\displaystyle n}$은 임의의 정수) 역시 ${\displaystyle z}$의 편각이다. 편각 중에서 구간 (${\displaystyle -\pi ,\pi }$]에 있는 것은 유일하며, 특별히 주편각이라고 한다. ${\displaystyle z}$의 편각을 나타내는 기호는 ${\displaystyle \mathrm {arg} \,z}$이며, 주편각은 ${\displaystyle \mathrm {Arg} \,z}$이다.

같이 보기

• 복소기하학
• 리만 구
• 실직선

참조

• Flanigan, Francis J. (1983). 《Complex Variables: Harmonic and Analytic Functions》. Dover. ISBN 0-486-61388-7.
• Moretti, Gino (1964). 《Functions of a Complex Variable》. Prentice-Hall.
• Wall, H. S. (1948). 《Analytic Theory of Continued Fractions》. D. Van Nostrand Company. Reprinted (1973) by Chelsea Publishing Company ISBN 0-8284-0207-8.
• Whittaker, E. T.; Watson, G. N. (1927). 《A Course in Modern Analysis》 Four판. Cambridge University Press.