튜링 기계

수학 또는 컴퓨터 과학에서 튜링 기계(영어: Turing machine)는 긴 테이프에 쓰여있는 여러 가지 기호들을 일정한 규칙에 따라 바꾸는 기계이다. 상당히 간단해 보이지만 이 기계는 적당한 규칙과 기호를 입력한다면 일반적인 컴퓨터의 알고리즘을 수행할 수 있으며 컴퓨터 CPU의 기능을 설명하는데 상당히 유용하다.

인공지능의 정도를 판별하는 테스트에 대해서는 튜링 테스트 문서를 참고하십시오.

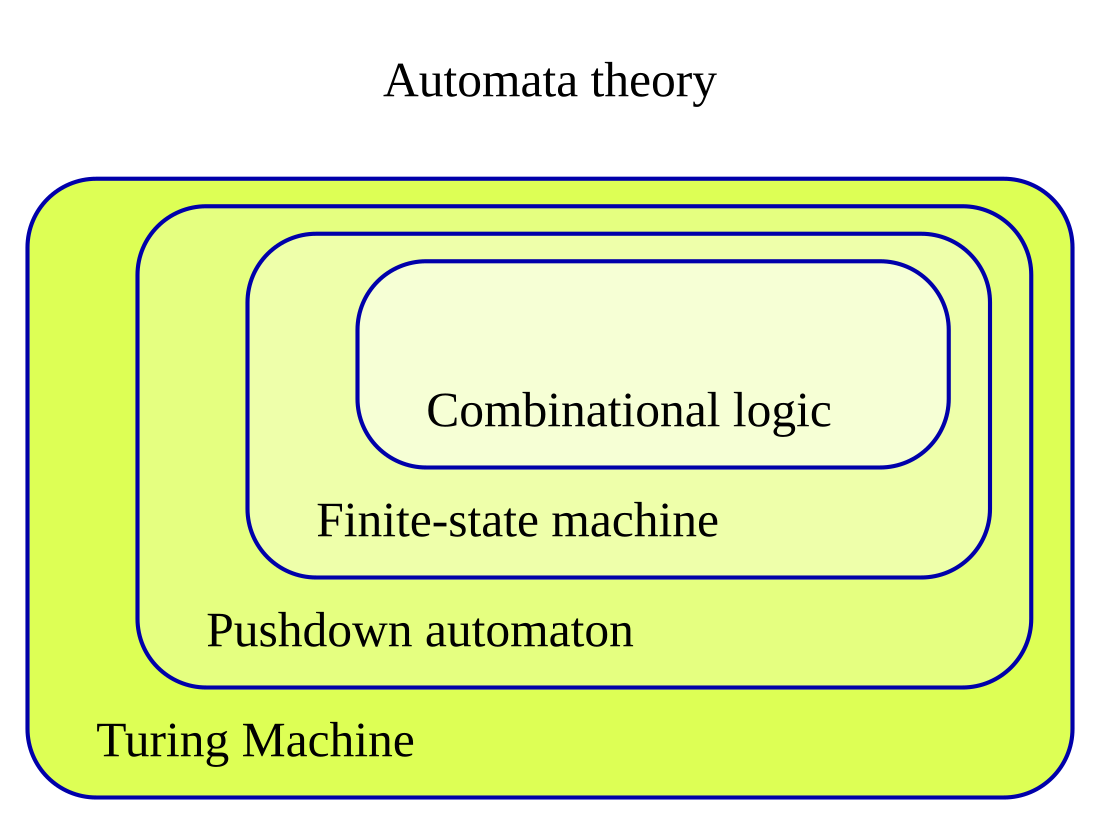
오토마타 벤 다이어그램

(각 레이어를 클릭하면 해당 글로 이동합니다.)

튜링 기계의 작동 방식을 묘사하는 그림임

1936년 앨런 튜링은 계산하는 기계를 대표할 수 있는 가상의 장치를 만들었고 ^[1] 이 장치에 영어 단어인 automatic의 a를 따서 "a-기계"라는 이름을 붙였다. 이 기계가 바로 나중에 창시자인 앨런 튜링의 이름을 따서 튜링 기계라 불리게 되었다.

1948년 "똑똑한 기계"라는 글에서 앨런 튜링은 자신의 "a-기계"를 간결히 정의하였다. 1936년 논문 "계산 가능한 수와 결정성 문제에의 응용"을 언급하며 튜링기계(이 글에서는 논리적 계산 기계라는 표현을 사용한다.)를 다음과 같이 기술하였다.

“	...무한한 저장공간은 무한한 길이의 테이프로 나타나는데 이 테이프는 하나의 기호를 인쇄할 수 있는 크기의 정사각형들로 쪼개져있다. 언제든지 기계속에는 하나의 기호가 들어가있고 이를 "읽힌 기호"라고 한다. 이 기계는 "읽힌 기호"를 바꿀 수 있는데 그 기계의 행동은 오직 읽힌 기호만이 결정한다. 테이프는 앞뒤로 움직일 수 있어서 모든 기호들은 적어도 한번씩은 기계에게 읽힐 것이다.	”
	— (튜링, 1948, p.61)

개론

튜링 기계는 수학적 모형의 일종으로, 특수한 테이프를 기반으로 작동하는 기계이다. 튜링 기계가 사용하는 테이프 위에는 테이프 머릿기호를 바탕으로 기계가 인식하거나 기록할 수 있는 기호들이 있다. 작동 방식은, “42번째 상태에서 0이라는 기호가 있다면 1을 쓴다. 1이라는 기호가 있다면 17번째 상태로 간다. 17번째 상태에서 0이라는 기호가 있다면 1을 쓰고, 1이라는 기호가 있다면 6번째 상태로 간다”와 같이 유한한 개수의 기초적 지시문으로 이루어진다. 원문(“계산가능수와 결정문제에 대한 응용에 관하여On computable numbers, with an application to the Entscheidungsproblem”)에 따르면 튜링이 상상한 것은 이러한 연산을 특출하게 수행할 수 있는 "컴퓨터"라 불릴 사람이었다.

더 자세히 설명하자면, 튜링 기계는 다음과 같은 부분들로 구성되어 있다.

1. 테이프 : 테이프는 서로 연속한 단위 구간들로 나뉜다. 각각의 구간은 알파벳을 가지고, 특정 알파벳은 비어있음을 나타낸다. 테이프는 왼쪽이나 오른쪽으로 임의적으로 확장될 수 있으며, 한번도 쓰이지 않은 구간은 비어있다는 기호로 표시된다. 어떤 테이프는 왼쪽을 고정시키고 오른쪽을 무한히 확장시키는 반직선의 형태로 되어있다.
2. 머리 : 기계가 머리를 읽으면 테이프를 왼쪽이나 오른쪽으로 한 칸 (오직 한 칸만) 이동시키는 역할을 한다. 다른 모델에서는 머리가 움직이고 테이프가 고정되기도 한다.
3. 상태 기록기는 튜링 기계의 유한히 많은 상태 중 하나를 기록한다. ‘개시 상태’는 상태 기록기를 초기화시키는 특별한 상태이다.
4. 유한한 표 (또는 행동표)는 특정한 상태(q_i)에 있는 기계가 어떠한 기호(a_j)를 읽을 때 해야 할 행동을 다음과 같이 지시한다(5튜플).
   1. 기호를 지우거나 적고 (a_j를 a_j1으로 치환)
   2. 머리를 옮긴다 (‘L’은 왼쪽으로 한 칸 가는 것을, ‘R’은 오른쪽으로 한 칸 가는 것을, ‘N’은 정지하고 같은 자리에 있는 것을 의미한다)
   3. 그리고 같은 상태나 새로운 상태로 간다 (q_i에서 q_i1으로)

튜링 기계가 가진 기호와 상태, 그리고 행동은 모두 유한하고 이산적이며, 구분 가능하다.

정의

호프크로프트와 일맨은 7투플의 단일 테이프 튜링 기계를 ${\displaystyle M=\left\langle Q,\Gamma ,b,\Sigma ,\delta ,q_{0},F\right\rangle }$로 정의했다. 각 변수들의 의미는 다음과 같다.

• ${\displaystyle Q}$는 유한하고 비어있지 않은 상태들의 집합
• ${\displaystyle \Gamma }$는 유한하고 비어있지 않은 기호와 알파벳들의 집합
• ${\displaystyle b\in \Gamma }$는 비어있음을 알려주는 기호 (테이프 위에서 유일하게 무한하게 나타날 수 있는 기호)
• ${\displaystyle \Sigma \subseteq \Gamma \backslash \left\{b\right\}}$는 입력가능한 기호들의 집합
• ${\displaystyle q_{0}\in Q}$는 초기상태
• ${\displaystyle F\subseteq Q}$는 최종상태, 또는 수락 상태
• ${\displaystyle \delta :Q\backslash F\times \Gamma \rightarrow Q\times \Gamma \times \left\{L,R\right\}}$는 부분함수

이 정의를 바탕으로 작동하는 모든 것은 튜링 기계라고 불린다.

튜링 기계를 실행하거나 실체화하기 위해 필요한 추가적인 요소

반 엠데 보아스(1990)에 따르면, “7투플의 이론적 구상은 기계의 행동과 계산의 극히 단적인 부분밖에 보여주지 못한다”라고 말했다. 예를 들면,

• 기호들을 실제로 결정하는 데 많은 과정이 소모될 것이다.
• 왼쪽이나 오른쪽으로 이동시키는 동작은 머리가 테이프 위에서 이동하게 할 수도 있지만, 실제로 튜링 기계를 만들 때 테이프가 머리 아래에서 왔다 갔다 하게 만드는 것이 더 현실적이다.
• 테이프는 유한하지만 필요한 만큼 비어있는 상태로 확장될 수 있다. 하지만 오히려 테이프가 무한하게 확장될 수 있고 유한한 분열의 머리가 채워져 있다고 보는 것이 더 타당하다.

다른 정의들

정의들은 설명을 위해 조금씩 다르게 표현되지만, 항상 같은 계산력을 가지도록 유도된다. 예를 들어, 집합 ${\displaystyle \left\{L,R\right\}}$를 ${\displaystyle \left\{L,R,N\right\}}$로 바꾸는 연산은 기계의 계산력을 높여주지 않는다. 가장 일반적인 정의는 튜링 기계의 지시를 튜링표로 표현한 것이다. 이것은 9개의 5투플로 구성되어 있다. (튜링(1936), 해독불가능에 대해서, p. 126-127과 데이비스(2000) p. 152)

(정의 1) : (q_j, S_j, S_k/E/N, L/R/N, q_m)

(현재의 상태 q_j, 읽힌 기호 S_j, 쓰이는 기호 S_k/지우기 E/아무것도 하지 않음 N, 한 칸 왼쪽으로 이동 L/오른쪽으로 이동 R/움직이지 않음 N, 새로운 상태 q_m)

다른 저자들 (민스키(1967), p. 119, 호프크로프트와 일맨 (1979) p. 158, 스톤 (1972) p. 9)은 새로운상태 qm이 읽힌 기호 Sj의 바로 뒤에 위치하게 함으로써 다른 정의를 취했다.

(정의 2) : (q_j, S_j, q_m, S_k/E/N, L/R/N)

(현재의 상태 q_i, 읽힌 기호 S_j, 새로운 상태 q_m, 쓰이는 기호 S_k/지우기 E/아무것도 하지 않음 N, 한 칸 왼쪽으로 이동 L/오른쪽으로 이동 R/움직이지 않음 N)

이 글의 나머지 부분에 대해서는 “정의 1” (튜링/데이비스 정의)를 사용할 것이다.

예시 : 3-상태 2-기호의 아주 바쁜 기계를 5투플로 표현한 상태표
현재 상태	읽힌 기호	쓰이는 기호	이동 종류	최종(다음) 상태	5투플 표현
A	0	1	R	B	(A, 0, 1, R, B)
	1	1	L	C	(A, 1, 1, L, C)
B	0	1	L	A	(B, 0, 1, L, A)
	1	1	R	B	(B, 1, 1, R, B)
C	0	1	L	B	(C, 0, 1, L, B)
	1	1	N	H	(C, 1, 1, N, H)

다음 표에서 볼 수 있듯이, 튜링의 본래 모델은 N1, N2, N3라고 불리는 세 가지의 행동만을 허용했다. 예를 들어, 읽힌 구간의 지우기를 0번째 기호인 S₀=”지움” 또는 “비어있음” 등으로 표현하는 것은 허용했으나 아무것도 쓰지 않는 것은 허용하지 않았기 때문에 모든 행동에는 “기호 S_k를 인쇄한다” 또는 “지운다”라는 명령이 포함되어 있었다. 약어들은 튜링이 만든 것인데, 튜링의 원문이 나온 이후 기계 모델은 9가지의 5투플을 포함하고 있다.

	현재 m-배형 (튜링 상태)	테이프 기호	인쇄	테이프 행동	최종 m-배형 (튜링 상태)	5투플	5투플 주석	4투플
N1	qi	Sj	Print(Sk)	Left L	qm	(qi, Sj, Sk, L, qm)	"blank" = S0, 1=S1, etc.
N2	qi	Sj	Print(Sk)	Right R	qm	(qi, Sj, Sk, R, qm)	"blank" = S0, 1=S1, etc.
N3	qi	Sj	Print(Sk)	None N	qm	(qi, Sj, Sk, N, qm)	"blank" = S0, 1=S1, etc.	(qi, Sj, Sk, qm)
4	qi	Sj	None N	Left L	qm	(qi, Sj, N, L, qm)		(qi, Sj, L, qm)
5	qi	Sj	None N	Right R	qm	(qi, Sj, N, R, qm)		(qi, Sj, R, qm)
6	qi	Sj	None N	None N	qm	(qi, Sj, N, N, qm)	Direct "jump"	(qi, Sj, N, qm)
7	qi	Sj	Erase	Left L	qm	(qi, Sj, E, L, qm)
8	qi	Sj	Erase	Right R	qm	(qi, Sj, E, R, qm)
9	qi	Sj	Erase	None N	qm	(qi, Sj, E, N, qm)		(qi, Sj, E, qm)

어떠한 종류의 튜링표도 위의 아홉 개의 5투플로부터 조합될 수 있다. 기술적인 이유로 세 개의 “N” 지시는 무시되기도 한다. 반면, 4투플은 잘 사용되지 않는다. 이들은 튜링 지시를 단순화할 때 사용된다.

상태

튜링 기계를 설명하는 데 있어서 상태라는 말은 두 가지의 뜻을 가진다. 대부분의 경우는 현재 지시의 이름이나 내용을 뜻한다(상태 기록기에 저장된 정보). 하지만 튜링 (1936)은 계산과정 상에서 기계의 m배열과 기계의 진행 상태를 확실하게 구분했다. 튜링이 “상태식”이라 표현했던 것은 현재의 지시와 테이프 상의 모든 기호들을 포함한다.

“	따라서 튜링 기계가 수행하는 모든 단계에서 계산의 진행 상태는 지시와 테이프의 기호에 따라 결정된다. 즉, 시스템의 상태는 테이프 위에 존재하는 기호들의 나열로 표현된 하나의 식과 지시로 표현된다. 이 식을 “상태식”이라고 부른다.	”
	— 해독불가능에 관해서, p.139-140, 강조가 포함됨

튜링 기계의 “상태” 모식도

3-상태 아주 바쁜 기계의 상태표 (“P”=1을 인쇄하거나 씀)
테이프 기호	현재 상태 A			현재 상태 B			현재 상태 C
	쓰이는 기호	테이프 이동	다음 상태	쓰이는 기호	테이프 이동	다음 상태	쓰이는 기호	테이프 이동	다음 상태
0	P	R	B	P	L	A	P	L	B
1	P	L	C	P	R	B	P	R	HALT

3-상태 아주 바쁜 기계의 튜링 기계를 유한 오토마타에 입각해 표현해본 것. 각각의 원은 표의 상태를 나타내고, m배열, 지시, 또는 명령은 화살표로 표현된다. 화살표 위의 표식은 특정한 변화를 야기하는 ‘읽히는 기호’를 결정하고 슬래쉬 뒤의 동작은 따라오는 행동을 의미한다. 이 정의는 맥클럭시(1965), 부스(1967), 힐 그리고 피터슨에 의해 보여졌다.

이러한 모식도들은 일련의 계산 궤적을 나타내는 것이 아니라 순간을 포착해서 보여주는 것이다. 아주 바쁜 기계는 작동하는 동안 항상 동일한 궤적을 따라 진행하지만 다른 유사한 기계의 경우에는 아닐 수도 있다.

튜링 머신과 동치인 다른 모델들

단순한 범용 튜링 기계보다 더 높은 계산능력을 지니고 있는 기계가 존재할 것이라는 주장이 있었지만, 그러한 가상 기계들은 결국 범용 튜링 기계와 같은 능력을 가지고 있다는 사실이 증명되었다(홉크로프트와 울만, p. 159, cf Minsky(1967)). 그 기계들이 더 높은 속도와 적은 저장 공간을 가질지언정, 범용 튜링 기계보다 더 많은 수학적 함수들을 계산 할 수는 없다는 것이다.(처치-튜링 명제는 모든 기계가 이러한 법칙을 따를 것이라고 주장한다. 즉 모든 계산 가능한 문제는 튜링 기계로 계산할 수 있으며, 그 역 역시 성립한다는 의미이다.)

몇 개의 다른 모델들도 튜링 기계와 동일한 계산 능력을 가지고 있다는 것이 밝혀졌다. 그중에는 다중 테이프 튜링 기계, 다중 트랙 튜링 기계, 입력과 출력이 있는 튜링 기계, 비결정론적 튜링 기계 등이 있다.

범용 튜링 기계

튜링은 미결정성에 다음과 같이 적었다.

“

계산 가능한 수열을 계산하는 단일 기계를 만들 수 있다. 만약 이 기계 U에 들어온 테이프의 처음 부분이 어떤 계산기계 M이 처리한 세미콜론(;)으로 분할된 5-튜플이라면 U는 M과 똑같은 계산 과정을 거치게 된다.

”

지금은 이 발견이 당연하다고 생각하지만 그 당시(1936)로서는 정말 놀라운 발견이었다. 일부 학자들은 튜링이 범용 기계(Universal Machine)"이라고 부른 이 계산 모델이 프로그램 내장식 컴퓨터를 위한 기초적인 이론적 해결책을 제시했다고 생각한다.

“	튜링의 논문은...기본적으로 현대 컴퓨터와 관련된 일부 프로그래밍 기술의 발견을 서술하고 있다.	”
	— 민스키(1967) p.104

계산복잡도의 측면에서 보면 다중테이프 튜링 기계는 이 기계가 시뮬레이트하는 기계에 비해 로그 인수만큼 느려야 한다. 이 결과는 1966년에 F.C. 헨리와 R.E. 스턴에 의해 얻어졌다.(아오라와 바락, 2009, 정리 1.9)

실제 기계와의 비교

흔히들 튜링 기계는 다른 오토마타와 다르게 실제 기계만큼 강력하고 실제 프로그램이 할 수 있는 연산을 모두 실행할 수 있다고 한다. 여기서 간과하고 있는 사실은 실제 기계는 유한개의 배형만을 가질 수 있기 때문에 이 "실제 기계"는 선형 구속 오토마타에 그친다. 그에 비해 튜링 기계는 연산을 위한 무한한 저장 공간을 가진 기계이다. 튜링 기계는 컴퓨터를 모델링한 것이 아니라 연산 자체를 모델링한 것이다. 역사적으로 보자면 고정된 내부 저장장치를 이용해 연산하는 컴퓨터는 튜링 기계보다 훨씬 나중에 개발되었다.

튜링 기계는 다음과 같은 이유들로 실제 컴퓨터의 모형으로서 상당히 유용하다.

1. 실제 컴퓨터가 연산할 수 있다면 튜링 기계 역시 마찬가지이다. 그렇기에 튜링 기계의 한계는 곧 실제 컴퓨터에도 적용된다.
2. 실제 컴퓨터와 튜링 기계의 차이점은 처리할 수 있는 데이터의 양이다. 튜링 기계의 경우 무한한 양의 데이터를 처리할 수 있으나, 실제 컴퓨터가 처리할 수 있는 데이터의 양은 유한하다. 하지만 유한한 시간에서는 튜링 기계도 실제 기계처럼 유한한 양의 데이터만 조작 가능하다.
3. 튜링 기계처럼 실제 기계도 하드 디스크와 같은 기타 저장 매체들을 이용해 저장 공간을 확장시킬 수 있다. 따라서 이런 저장 매체들이 구하기 힘들어진다면 튜링 기계와 실제 기계의 격차는 벌어질 것이다. 하지만 연산들이 실패하는 이유는 대부분 저장 공간의 작은 크기가 아닌 느린 연산 속도이다.
4. 실제 기계를 설명할 때 더 단순하고 추상적인 모델을 사용한 실제 설명보다 튜링 기계를 이용한 설명이 더욱 간단하다. 만약 튜링 기계가 하나의 알고리즘을 설명하는데 몇 백개 정도의 상태가 필요하다면 같은 설명을 하는데 결정적 유한 오토마타는 수 천조의 상태가 필요하다.
5. 튜링 기계는 얼마나 많은 메모리를 사용하는지에 관계없이 알고리즘을 설명할 수 있다. 튜링 기계는 실제 기계의 발전과 전혀 관계 없이 알고리즘에 대한 이론적인 설명이 가능하다.
6. 튜링 기계는 알고리즘의 설명을 간단케 한다. 튜링 동치인 추상적 기계를 사용하여 알고리즘을 실행하는 것은 실제 기계보다 훨씬 일반적이다. 실제 기계에는 메모리 공간 부족과 같은 특수한 상황이 존재하며 또 자료의 종류가 한정되어 있기 때문이다.

하지만 튜링 기계도 어떤 경우에는 실제 프로그램에 대한 좋지 못한 모델이 될 수 있다. 운영 체제나 워드 프로세서 같은 경우에는 시간에 따라 무한한 입력을 받을 수 있어야 하는데 튜링 기계는 그러한 무한한 연산의 경우 모델링이 힘들다.(그렇지만 역시 부분적인 과정들은 모델링할 수 있다.)

튜링 기계의 한계(시간 복잡도 이론)

튜링 기계의 한계는 일부 배열들의 능력을 잘 모델링하지 못한다는 것이다. 현대의 저장 프로그램 컴퓨터들은 추상적인 랜덤 접근 저장 프로그램 기계(Random Access Store Program Machine, RASP machine)들의 실질적인 예이다. 범용 튜링 기계와 같이 RASP는 무한개의 구분 가능한, 동시에 셀 수 있지만 무한한 레지스터(정수를 하나 저장할 수 있는 메모리 공간)를 가지고 있다. RASP의 유한 상태 기계는 하나의 레지스터가 다른 레지스터의 주소를 포함하는 등 간접적으로 주소를 저장하는 것이 가능하다. 따라서 RASP의 프로그램은 레지스터 배열에 있는 다른 레지스터를 호출하는 것이 가능하다. 메모리 인덱스를 이용한 연산의 최적화가 튜링 기계에서는 불가능하므로 튜링 기계로 모델링 할 때 일부 알고리즘에 대해서는 시간복잡도의 잘못된 하한을 줄 수 있다. 예를 들어 이진 검색 알고리즘의 경우 튜링 기계 모델보단 RASP 모델로 훨씬 더 빠르게 연산이 가능하다.

역사

 알고리즘 및 처치-튜링 명제 문서를 참고하십시오.

역사적 배경 : 계산 기계

앨런 튜링(1912-1954)의 제자이자 평생의 친구인 로빈 간디(1919-1995)는 '계산 기계(calculatng machine)'의 관념의 기원을 배비지에서 찾았으며 실제로 배비지 이론을 제안했다.

간디는 배비지의 해석 기관을 다섯 개의 연산으로 묘사했다.

1. 산술적 함수 +, -, × (이 때의 -는 y≥0 일 때 x-y=0이 되는 적절한 뺄셈이다.)
2. 그 어떤 일련의 연산도 하나의 연산으로 표현될 수 있다.
3. 반복 (연산 P를 n번 반복)
4. 조건부 반복 (시험 T가 성공한다는 조건 하에 연산 P를 n번 반복)
5. 조건부 이동 (결과값에 따라 계산 순서가 변경)

간디는 1, 2, 4에 의해 계산될 수 있는 함수를 계산 가능한 함수로 정의했다.

판정문제

 이 부분의 본문은 판정문제입니다.

1900년 수학자 다비트 힐베르트가 제안한 힐베르트의 문제들 중 열 번째 문제는 그 개념이 정립되기 이전에 거의 30년 가까이 해결되지 않은 채 표류했다. 힐베르트의 열 번째 문제는 다음과 같다.

10. 디오판토스 방정식의 풀이 가능성을 결정하라.
임의의 주어진 디오판토스 방정식의 정수해를 유한한 연산을 통해 얻어낼 수 있는가?

1928년 힐베르트는 다음의 세 물음을 통해 자신의 문제를 좀 더 엄밀하게 만들었다.

1. 수학은 완전한가?
2. 수학은 모순을 포함하지 않는가?
3. 수학은 결정 가능한가?

첫 번째와 두 번째 문제는 1930년 쿠르트 괴델에 의해 해결되었으나, 세 번째 문제는 1930년대 중반까지 해결되지 않았다.

앨런 튜링의 a-기계

1935년 봄, 케임브리지 킹스 칼리지의 젊은 박사 과정 학생이었던 튜링은 한 과제에 직면했다. 그는 논리학자 뉴먼의 강의에 자극을 받았으며, 결정 문제에 대한 괴델의 연구에 대해서 알게 되었다. 뉴먼은 '기계적'이라는 단어를 사용했으며, 1955년 튜링의 부고에 뉴먼은 다음과 같이 기술했다.

"‘기계적' 과정이란 무엇인가?’라는 질문에 튜링은 '기계로 할 수 있는 것'이라는 답을 내놓았다.

— Gandy, p.74

튜링은 그의 일생동안 기계에 대한 흥미를 가지고 있었다. 아래에도 나와있지만, 튜링은 그의 박사후과정 동안 불 논리 곱셈 기계를 만들었다. 그의 박사후과정 논문인 'Systems of Logic Based on Ordinals'는 계산 가능한 함수에 대한 다음의 정의를 담고 있다.

“	우리는 어떤 함수의 값이 순수한 기계적 과정을 통해 계산될 수 있을 때 그 함수를 계산 가능한 함수로 정의한다.	”
	— Turing(1939) in The Undecidable, p.160

튜링이 영국으로 돌아왔을 때, 그는 독일의 암호 기계인 '에니그마 the Enigma'를 해독하기 위한 방법을 구상하는 것에 참여했다. 그는 ACE(Automatic Computing Engine)의 개발에 참여하기도 했다.

1937-1970 : 디지털 컴퓨터, 그리고 컴퓨터 과학의 탄생

1937년, 그의 박사후 과정을 위해 프린스턴에서 연구하는 동안 튜링은 전기-기계식 릴레이를 이용해 디지털(Boolean-logic) 곱셈 기계를 만들었다. 튜링의 발명은 단순한 호기심과 실험 정신에 의해 시작되었지만, 같은 방향을 향하는 연구들이 독일과 미국에서 행해지고 있었으며, 그러한 노력의 결과물은 2차 세계 대전 동안 연합국과 주축국의 군사 활동에 사용되었다. 1950년대 중반 하오 왕과 마빈 민스키는 튜링 기계를 좀 더 간단한 형태로 바꾸었다. 동시에 유럽의 연구자들은 최신식의 전자 컴퓨터를 현재의 튜링 기계인 '컴퓨터와 같은 이론적 오브젝트'로 환원시켜 생각했다. 1950년대 후반에서 1960년대 초반에 멜자크와 레벡(1961), 민스키(1961), 셰퍼슨과 스터기스(1961) 등의 유럽 연구자들은 일련의 연구들을 통해 튜링 기계를 좀 더 친숙하고 컴퓨터와 같은 '셈 기계 counter machine'로 만들었다. 이후 1970년대 초반에는 엘곳과 로빈슨(1964), 할트마니스(1971), 쿡과 렉하우(1973) 등은 이 연구를 진척시켜 '기록 기계 register machine'와 RAM의 모델로 발전시켰다.

1970-현재 : 계산 모델로서의 튜링 기계

오늘날의 셈 기계, 기록 기계, 그리고 RAM은 그 근간을 튜링 기계에 두고 있으며, 수많은 연구자들은 계산 이론을 풀어나가는 데에 있어서 튜링 기계를 사용한다. 특히 계산 복잡도 이론의 경우 튜링 기계의 사용이 필수적이다.

같이 보기

• 확률적 튜링 기계
• 양자 튜링 기계
• 교대 튜링 기계
• 범용 튜링 기계(UTM, en:Universal Turing machine)

참고

1. 1935년 중반, 막스 뉴만은 그의 강의에서 "과연 수학적 표현에 적용되어 그 표현이 증명될 수 있는지를 알려주는 명확한 방법이(뉴만은 이를 기계적 과정이라고 표현하였다.) 존재하는가?"(호지스 1983:93) 라는 질문을 던졌다. 이 강의를 들고 튜링은 그 가상의 장치를 생각해내었다고 한다.(더 자세한 사실은 역사부분을 참조하시오) 그는 이 논문을 런던 수학회지에 1936년 5월 31일에 제출하였으나(참고: 호지스 1983:112), 정작 이 논문이 출판된 것은 1937년 초였고, 그 해 2월이 다 돼서야 발췌 인쇄가 가능해졌다.(참고: 호지스 1983:129)

참고 문헌

1차 저서, 재출판, 편집

• B. Jack Copeland ed. (2004), The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life plus The Secrets of Enigma, Clarendon Press (Oxford University Press), Oxford UK, ISBN 0-19-825079-7. Contains the Turing papers plus a draft letter to Emil Post re his criticism of "Turing's convention", and Donald W. Davies' Corrections to Turing's Universal Computing Machine
• 마틴 데이비스 (ed.) (1965), 해독불가능에 대해서, Raven Press, Hewlett, NY.
• 에밀 포스트 (1936), "Finite Combinatory Processes—Formulation 1", Journal of Symbolic Logic, 1, 103–105, 1936. 해독불가능에 대해서에 재출판됨. pp. 289ff.
• 에밀 포스트 (1947), "Recursive Unsolvability of a Problem of Thue", Journal of Symbolic Logic, vol. 12, pp. 1–11. 해독불가능에 대해서 재출판됨. pp. 293ff. In the Appendix of this paper Post comments on and gives corrections to Turing's paper of 1936–1937. In particular see the footnotes 11 with corrections to the universal computing machine coding and footnote 14 with comments on Turing's first and second proofs.
• 튜링, A.M. (1936). “계산가능수와 결정문제에 대한 응용에 관하여”. 《런던수학회지》. 2 (1937) 42: 230–65. doi:10.1112/plms/s2-42.1.230. (and 튜링, A.M. (1938). “계산가능수와 결정문제에 대한 응용에 관하여: 수정판”. 《런던수학회지》. 2 (1937) 43 (6): 544–6. doi:10.1112/plms/s2-43.6.544.). Reprinted in many collections, e.g. in 해독불가능에 대해서 pp. 115–154; available on the web in many places, e.g. at Scribd.
• 앨런 튜링, 1948, "Intelligent Machinery." Reprinted in "Cybernetics: Key Papers." Ed. C.R. Evans and A.D.J. Robertson. Baltimore: University Park Press, 1968. p. 31.
• F. C. Hennie and R. E. Stearns. Two-tape simulation of multitape Turing machines. JACM, 13(4):533–546, 1966.

계산 이론

• 불로스, 조지; 리차드 제퍼리 (1989, 1999). 《Computability and Logic》 3판. Cambridge UK: Cambridge University Press. ISBN 0-521-20402-X. 더 이상 지원되지 않는 변수를 사용함 (도움말); 다음 날짜 값 확인 필요: |date= (도움말)
• 불로스, 조지; 존 부르게스, 리차드 제퍼리, (2002). 《Computability and Logic》 4판. Cambridge UK: Cambridge University Press. ISBN 0-521-00758-5 (pb.) |isbn= 값 확인 필요: invalid character (도움말). 더 이상 지원되지 않는 변수를 사용함 (도움말) Some parts have been significantly rewritten by Burgess. Presentation of Turing machines in context of Lambek "abacus machines" (cf Register machine) and recursive functions, showing their equivalence.
• 테일러 L. 부스 (1967), Sequential Machines and Automata Theory, John Wiley and Sons, Inc., New York. 공대 졸업생 수준의 책. 넓은 범위의 주제를 다루며 9장 튜링 기계는 재귀 이론에 대해서 조금 다루고 있다.
• 마틴 데이비스 (1958). 《Computability and Unsolvability》. McGraw-Hill Book Company, Inc, New York.. On pages 12–20 he gives examples of 5-tuple tables for Addition, The Successor Function, Subtraction (x ≥ y), Proper Subtraction (0 if x < y), The Identity Function and various identity functions, and Multiplication.
• 데이비스, 마틴; 론 시갈, 엘레인 J. 웨커 (1994). 《Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science》 2판. San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1. 더 이상 지원되지 않는 변수를 사용함 (도움말)
• Hennie, Fredrick (1977). 《Introduction to Computability》. Addison–Wesley, Reading, Mass. 지원되지 않는 변수 무시됨: |unused_data= (도움말). On pages 90–103 Hennie discusses the UTM with examples and flow-charts, but no actual 'code'.
• 존 홉크로프트와 제퍼리 울만, (1979). 《Introduction to Automata Theory, Languages and Computation》 1판. Addison–Wesley, Reading Mass. ISBN 0-201-02988-X. |isbn= 값 확인 필요: invalid character (도움말). A difficult book. Centered around the issues of machine-interpretation of "languages", NP-completeness, etc.
• Hopcroft, John E.; Rajeev Motwani, Jeffrey D. Ullman (2001). 《Introduction to Automata Theory, Languages, and Computation》 2판. Reading Mass: Addison–Wesley. ISBN 0-201-44124-1. 더 이상 지원되지 않는 변수를 사용함 (도움말) Distinctly different and less intimidating than the first edition.
• Stephen Kleene (1952), Introduction to Metamathematics, North–Holland Publishing Company, Amsterdam Netherlands, 10th impression (with corrections of 6th reprint 1971). Graduate level text; most of Chapter XIII Computable functions is on Turing machine proofs of computability of recursive functions, etc.
• Knuth, Donald E. (1973). 《Volume 1/Fundamental Algorithms: The Art of computer Programming》 2판. Reading, Mass.: Addison–Wesley Publishing Company.. With reference to the role of Turing machines in the development of computation (both hardware and software) see 1.4.5 History and Bibliography pp. 225ff and 2.6 History and Bibliographypp. 456ff.
• Zohar Manna, 1974, Mathematical Theory of Computation. Reprinted, Dover, 2003. ISBN 978-0-486-43238-0
• 마빈 민스키, Computation: Finite and Infinite Machines, Prentice–Hall, Inc., N.J., 1967. See Chapter 8, Section 8.2 "Unsolvability of the Halting Problem." 초보자도 읽을만 하며 재밌는 부분도 있다.
• Christos Papadimitriou (1993). 《Computational Complexity》 1판. Addison Wesley. ISBN 0-201-53082-1. Chapter 2: Turing machines, pp. 19–56.
• Michael Sipser (1997). 《Introduction to the Theory of Computation》. PWS Publishing. ISBN 0-534-94728-X. Chapter 3: The Church–Turing Thesis, pp. 125–149.
• 스톤, 해롤드 S. (1972). 《Introduction to Computer Organization and Data Structures》 1판. New York: McGraw–Hill Book Company. ISBN 0-07-061726-0.
• Peter van Emde Boas 1990, Machine Models and Simulations, pp. 3–66, in Jan van Leeuwen, ed., Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity, The MIT Press/Elsevier, [place?], ISBN 0-444-88071-2 (Volume A). QA76.H279 1990. Valuable survey, with 141 references.

처치-튜링 명제

• Nachum Dershowitz; Yuri Gurevich (2008년 9월). “A natural axiomatization of computability and proof of Church's Thesis” (PDF). 《Bulletin of Symbolic Logic》 14 (3). 2008년 10월 15일에 확인함. 더 이상 지원되지 않는 변수를 사용함 (도움말)
• Roger Penrose (1989, 1990). 《The Emperor's New Mind》 2판. Oxford University Press, New York. ISBN 0-19-851973-7. 다음 날짜 값 확인 필요: |date= (도움말)

작은 튜링 기계

• Rogozhin, Yurii, 1998, "A Universal Turing Machine with 22 States and 2 Symbols", Romanian Journal Of Information Science and Technology, 1(3), 259–265, 1998. (surveys known results about small universal Turing machines)
• Stephen Wolfram, 2002, A New Kind of Science, Wolfram Media, ISBN 1-57955-008-8
• Brunfiel, Geoff, Student snags maths prize, Nature, October 24. 2007.
• Jim Giles (2007), Simplest 'universal computer' wins student $25,000, New Scientist, October 24, 2007.
• Alex Smith, Universality of Wolfram’s 2, 3 Turing Machine, Submission for the Wolfram 2, 3 Turing Machine Research Prize.
• Vaughan Pratt, 2007, "Simple Turing machines, Universality, Encodings, etc.", FOM email list. October 29, 2007.
• 마틴 데이비스, 2007, "Smallest universal machine", and Definition of universal Turing machine FOM email list. October 26–27, 2007.

• Alasdair Urquhart, 2007 "Smallest universal machine", FOM email list. October 26, 2007.
• Hector Zenil (Wolfram Research), 2007 "smallest universal machine", FOM email list. October 29, 2007.
• Todd Rowland, 2007, "Confusion on FOM", Wolfram Science message board, October 30, 2007.

기타

• 마틴 데이비스 (2000). 《Engines of Logic: Mathematicians and the origin of the Computer》 1판. W. W. Norton & Company, New York. ISBN 0-393-32229-7 pbk. |isbn= 값 확인 필요: invalid character (도움말).
• 로빈 간디, "The Confluence of Ideas in 1936", pp. 51–102 in Rolf Herken, see below.
• 스티븐 호킹 (editor), 2005, God Created the Integers: The Mathematical Breakthroughs that Changed History, Running Press, Philadelphia, ISBN 978-0-7624-1922-7. Includes Turing's 1936–1937 paper, with brief commentary and biography of Turing as written by Hawking.
• Rolf Herken (1995). 《The Universal Turing Machine—A Half-Century Survey》. Springer Verlag. ISBN 3-211-82637-8.
• 앤드류 호지스, Alan Turing: The Enigma, Simon and Schuster, New York. Cf Chapter "The Spirit of Truth" for a history leading to, and a discussion of, his proof.
• Ivars Peterson (1988). 《The Mathematical Tourist: Snapshots of Modern Mathematics》 1판. W. H. Freeman and Company, New York. ISBN 0-7167-2064-7 (pbk.) |isbn= 값 확인 필요: invalid character (도움말).
• Paul Strathern (1997). 《Turing and the Computer—The Big Idea》. Anchor Books/Doubleday. ISBN 0-385-49243-X.
• Hao Wang, "A variant to Turing's theory of computing machines", Journal of the Association for Computing Machinery (JACM) 4, 63–92 (1957).
• Charles Petzold, Petzold, Charles, The Annotated Turing, John Wiley & Sons, Inc., ISBN 0-470-22905-5
• Arora, Sanjeev; Barak, Boaz, "Complexity Theory: A Modern Approach", Cambridge University Press, 2009, ISBN 978-0-521-42426-4, section 1.4, "Machines as strings and the universal Turing machine" and 1.7, "Proof of theorem 1.9"
• Isaiah Pinchas Kantorovitz, "A note on turing machine computability of rule driven systems", ACM SIGACT News December 2005.

외부 링크

• Turing Machine on Stanford Encyclopedia of Philosophy
• Detailed info on the Church–Turing Hypothesis (Stanford Encyclopedia of Philosophy)
• Turing Machine-Like Models in Molecular Biology, to understand life mechanisms with a DNA-tape processor.
• The Turing machine—Summary about the Turing machine, its functionality and historical facts
• The Wolfram 2,3 Turing Machine Research Prize—Stephen Wolfram's $25,000 prize for the proof or disproof of the universality of the potentially smallest universal Turing Machine. The contest has ended, with the proof affirming the machine's universality.
• "Turing Machine Causal Networks" by Enrique Zeleny, Wolfram Demonstrations Project.
• (영어) Turing Machines - Curlie
• Purely mechanical Turing Machine