이진 유리수

수학에서 이진 유리수(二進有理數, dyadic rational) 또는 이진 분수(二進分數, dyadic fraction)는 이진법 전개가 유한한 유리수이다. 즉, 분자가 정수, 분모가 2의 거듭제곱인 분수로 나타낼 수 있는 유리수이다. 예를 들어, 1/2, 3/8은 이진 유리수이며, 1/3은 이진 유리수가 아니다.

0부터 1까지의 이진유리수

정의

이진 유리수는 다음과 같은 꼴의 수이다.

${\displaystyle {\frac {a}{2^{b}}}\qquad (a,b\in \mathbb {Z} ,\;b\geq 0)}$

성질

연산에 대한 닫힘

두 이진 유리수의 합·차·곱 역시 이진 유리수이다.

${\displaystyle {\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}={\frac {2^{d-b}a+c}{2^{d}}}\qquad (b\leq d)}$

${\displaystyle {\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}={\frac {2^{d-b}a-c}{2^{d}}}\qquad (b\leq d)}$

${\displaystyle {\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}={\frac {a-2^{b-d}c}{2^{b}}}\qquad (b>d)}$

${\displaystyle {\frac {a}{2^{b}}}\times {\frac {c}{2^{d}}}={\frac {ac}{2^{b+d}}}}$

그러나, 두 이진 유리수의 몫은 이진 유리수가 아닐 수 있다.

${\displaystyle {\frac {a}{2^{b}}}\div {\frac {c}{2^{d}}}={\frac {2^{d-b}a}{c}}\qquad (b\leq d)}$

${\displaystyle {\frac {a}{2^{b}}}\div {\frac {c}{2^{d}}}={\frac {a}{2^{b-d}c}}\qquad (b>d)}$

대수적 성질

이진 유리수의 집합은 유리수환의 부분환을 이루며, 이 부분환은 정수환의 2의 거듭제곱의 곱셈 모노이드에 대한 국소화 ${\displaystyle \{2^{n}\colon n\in \mathbb {N} \}^{-1}\mathbb {Z} }$이다. 이진 유리수의 덧셈군의 정수 덧셈군에 대한 몫군은 프뤼퍼 2-군과 동형이다.

순서론적 성질

임의의 가산 전순서 집합은 항상 ${\displaystyle \{a/2^{b}\in [0,1]\colon a,b\in \mathbb {Z} ,\;b\geq 0\}}$의 부분 집합과 동형이다.

위상수학적 성질

이진 유리수들은 실수선의 조밀 집합을 이룬다. 구체적으로, 임의의 실수 ${\displaystyle x\in \mathbb {R} }$를 이진 유리수열 ${\displaystyle (\lfloor 2^{n}x\rfloor /2^{n})_{n=0}^{\infty }}$로 얼마든지 가깝게 근사할 수 있다.

응용

초현실수는 유한 이진 분수를 만든 후 무한대, 무한소 그리고 다른 수들을 만들어 내는 구성 규칙을 반복하여 만들어진다.

이진 반 데르 코르푸트 수열은 양의 이진 유리수의 균등 분배적인 순열이다.

이진 유리수는 우리손의 보조정리를 비롯한 명제들의 증명에서 응용된다.

측량

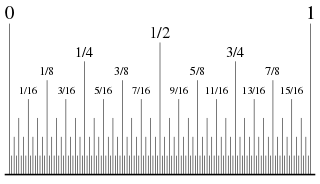
인치의 소수부분은 습관상 이진분수로 표시한다. 고대 이집트인들도 측량에 분모가 64 이하인 이진분수를 사용하였다.^[1]

음악

박자표는 관례적으로 이진분수로 이루어진 서양 기보법이다. 20세기쯤 비이진법적 박자표가 작곡가들에 의해 도입되었지만 말이다.

같이 보기

• 반정수는 홀수를 2로 나눠 얻어지는 수이며, 이진 유리수의 특수한 경우이다.
• 2진수는 이진 유리수를 확장한 수 체계이다.

각주

1. Curtis, Lorenzo J. (1978), “Concept of the exponential law prior to 1900”, 《American Journal of Physics》 (영어) 46 (9): 896–906, doi:10.1119/1.11512.