ಘನ (ಆಕೃತಿ)

ಈ article the geometric shape ಬಗ್ಗೆ. other uses ಗಾಗಿ, ಘನ (ಆಕೃತಿ) (disambiguation) ನೋಡಿ.

ಟೆಂಪ್ಲೇಟು:Reg polyhedron stat table ರೇಖಾಗಣಿತದಲ್ಲಿ, ಒಂದು ಕ್ಯೂಬ್ (ಘನ)ಎಂಬುದು ಒಂದು ತ್ರಿವಿಮಿತೀಯ ಘನಾಕೃತಿಯ ವಸ್ತುವಾಗಿದೆ. ಇದು ಆರು ಚೌಕಾಕಾರದ ಮುಖಗಳು, ಪಾರ್ಶ್ವಗಳು ಅಥವಾ ಬದಿಗಳಿಂದ ಪರಿಮಿತಿಯನ್ನು ಹೊಂದಿದ್ದು, ಇದರಲ್ಲಿ ಮೂರು ಬದಿಗಳು ಪ್ರತಿ ಬಹುಭುಜದಲ್ಲಿ ಸೇರುತ್ತವೆ. ಘನವನ್ನು ಒಂದು ಸಾಮಾನ್ಯ ಷಣ್ಮುಖ (ಆರು ಮುಖಗಳಿರುವ ಒಂದು ಘನ ಕಾಯ)(ಹೆಕ್ಸಾಹೆಡ್ರಾನ್) ಎಂದೂ ಕರೆಯಬಹುದು ಜೊತೆಗೆ ಇದು ಐದು ಪ್ಲೇಟಾನಿಕ್ ಕಾಯಗಳಲ್ಲಿ ಒಂದೆನಿಸಿದೆ. ಇದೊಂದು ಆಯತಾಕೃತಿಯ ಸಮಾಂತರುಪರಿಪದಿ ಹಾಗು ತ್ರಿಕೋನೀಯ ಟ್ರಾಪೆಜೊಹೆಡ್ರಾನ್ ನ ವಿಶೇಷ ಬಗೆಯ ಚತುಷ್ಕೋನದ ಪ್ರಿಸಮ್(ಪಕ್ಕಗಳೆಲ್ಲವೂ ಸಮಾಂತರ ಚತುರ್ಭುಜಗಳಾಗಿಯೂ ಇರುವ ಘನ ಆಕೃತಿ) ಆಗಿದೆ. ಘನವು ಆಕ್ಟಹೆಡ್ರನ್(ಅಷ್ಟಮುಖಿಯ) ದ್ವಿರೂಪವಾಗಿದೆ. ಇದಕ್ಕೆ ಘನಾಕೃತಿಯ ಸಮಸೂತ್ರತೆಯಿದೆ (ಇದನ್ನು ಅಷ್ಟಮುಖೀಯ ಸಮಸೂತ್ರತೆ ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ).

ಒಂದು ಘನವು ಒಂದು ಹೈಪರ್ ಕ್ಯೂಬ್ ನ ಸಾಧಾರಣ ಕಲ್ಪನೆಯಲ್ಲಿ ಹೆಚ್ಚಿದ ತ್ರಿವಿಮಿತೀಯ ಮಾದರಿಯಾಗಿದೆ.

ಇದು 11 ಬಲೆಗಳಿಂದ ಸುತ್ತುವರೆಯಲ್ಪಟ್ಟಿರುತ್ತದೆ.^[೧] ಒಬ್ಬರು ಒಂದು ಘನಕ್ಕೆ ಬಣ್ಣ ಹಚ್ಚಬೇಕಾದರೆ, ಯಾವುದೇ ಎರಡು ಪಾರ್ಶ್ವ ಮುಖಗಳು ಒಂದೇ ಬಣ್ಣವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ, ಅದಕ್ಕೆ ಬಣ್ಣ ತುಂಬಬೇಕಾದರೆ 3 ಬಣ್ಣಗಳ ಅಗತ್ಯವಿದೆ.

ಮೂಲ ಘನದ ಅಂಚಿನ ಉದ್ದವು 1 ಆಗಿದ್ದರೆ, ಅದರ ದ್ವಿರೂಪದ ಆಕ್ಟಹೆಡ್ರನ್(ಅಷ್ಟಮುಖಿ) ಅಂಚಿನ ಉದ್ಧವು ${\displaystyle {\sqrt {2}}}$ ಆಗಿರುತ್ತದೆ.

ಕಾರ್ಟೇಸಿಯನ್ ನಿರ್ದೇಶಾಂಕ

ಮೂಲದಲ್ಲಿ ಕೇಂದ್ರೀಕೃತವಾದ, ಸ್ಥಿರಬಿಂದುವಿನೊಂದಿಗೆ ಸಮಾನಾಂತರವಾಗಿರುವ ಅಂಚುಗಳೊಂದಿಗೆ ಹಾಗು 2ರಷ್ಟು ಅಂಚಿನ ಉದ್ದವನ್ನು ಹೊಂದಿರುವ ಒಂದು ಘನಾಕೃತಿಗೆ, ಕಾರ್ಟೇಸಿಯನ್ ನಿರ್ದೇಶಾಂಕದ ಬಹುಭುಜಗಳು,

(±1, ±1, ±1)

ಈ ನಡುವೆ ಒಳಕೋನವು ಎಲ್ಲ ಬಿಂದುಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ (x ₀, x ₁, x ₂) ಜೊತೆಗೆ −1 < x _i < 1ನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ.

ಸೂತ್ರಗಳು

ಒಂದು ಘನದ ಅಂಚಿನ ಉದ್ದವು ${\displaystyle a}$ನಷ್ಟಿದ್ದರೆ,

ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ	${\displaystyle 6a^{2}}$
ಘನ ಅಳತೆ	${\displaystyle a^{3}}$
ಪಾರ್ಶ್ವ ಕರ್ಣರೇಖೆ	${\displaystyle {\sqrt {2}}a}$
ಸ್ಥಳ ಕರ್ಣರೇಖೆ	${\displaystyle {\sqrt {3}}a}$
ಪರಿವೃತ್ತ ಗೋಲದ ತ್ರಿಜ್ಯ	${\displaystyle {\frac {\sqrt {3}}{2}}a}$
ಅಂಚುಗಳ ಗೋಲ ಸ್ಪರ್ಶಕ ರೇಖೆಯ ತ್ರಿಜ್ಯ	${\displaystyle {\frac {a}{\sqrt {2}}}}$
ಗೋಲದ ಒಳಗಡೆ ರಚನೆಯಾದ ತ್ರಿಜ್ಯ	${\displaystyle {\frac {a}{2}}}$
ಘನವಸ್ತುಗಳ ತಲದ ನಡುವಿನ ಕೋನಗಳು	${\displaystyle {\frac {\pi }{2}}}$

ಒಂದು ಘನದ ಅಳತೆಯು ಅದರ ಬದಿಗಳ ಮೂರನೇ ಘಾತವಾದ ಕಾರಣ a ×a ×a , ಮೂರನೇ ಘಾತಗಳನ್ನು, ಚತುಷ್ಕೋನಗಳು ಹಾಗು ಎರಡನೇ ಘಾತಗಳ ಹೋಲಿಕೆಯೊಂದಿಗೆಘನಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಒಂದು ನಿರ್ದಿಷ್ಟ ಕ್ಷೇತ್ರ ತಲದಲ್ಲಿ ಒಂದು ಘನವು, ಘನಾಭ(ಕ್ಯೂಬಾಯ್ಡ್)(ಆಯಾಕೃತಿಯ ಬಾಕ್ಸ್ ಗಳು)ಗಳಲ್ಲೇ ಅತ್ಯಂತ ದೊಡ್ಡ ಘನ ಅಳತೆಯನ್ನು ಹೊಂದಿದೆ. ಅಲ್ಲದೆ, ಒಂದು ಘನವು, ಸಮಾನಾಂತರ ರೇಖೀಯ ಗಾತ್ರವನ್ನು ಒಳಗೊಂಡು ಘನಾಭಗಳಲ್ಲಿ ಅತ್ಯಂತ ದೊಡ್ಡ ಘನ ಅಳತೆಯನ್ನು ಹೊಂದಿದೆ(ಉದ್ದ + ಅಗಲ + ಎತ್ತರ).

ಏಕಪ್ರಕಾರದ ವರ್ಣಲೇಪನ ಹಾಗು ಸಮಸೂತ್ರತೆ(ಸಿಮಿಟ್ರಿ)

ಒಂದು ಘನವು 3 ಏಕಪ್ರಕಾರದ ವರ್ಣಲೇಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಇವುಗಳನ್ನು ಬಹುಮುಖಿಗಳ ಸುತ್ತಲೂ ಇರುವ ಚತುಷ್ಕೋನ ಮುಖಗಳಿಗೆ ಬಳಿಯಲಾದ ಬಣ್ಣಗಳನ್ನು ಆಧರಿಸಿ ಹೆಸರಿಸಲಾಗುತ್ತದೆ: 111, 112, 123.

ಘನವು ಸಮಸೂತ್ರತೆಯ 3 ವರ್ಗಗಳನ್ನು ಒಳಗೊಂಡಿದೆ, ಇದನ್ನು ಪಾರ್ಶ್ವಗಳಿಗೆ ಬಹುಮುಖಿ-ಸಕರ್ಮಕ ಬಣ್ಣವನ್ನು ಬಳಿಯುವ ಮೂಲಕ ನಿರೂಪಿಸಲಾಗಿದೆ. ಅತ್ಯಂತ ದೊಡ್ಡ ಆಕ್ಟಹೆಡ್ರಲ್(ಅಷ್ಟಮುಖಿ)ಸಮಸೂತ್ರತೆಯಲ್ಲಿ O_h ಎಲ್ಲ ಪಾರ್ಶ್ವಗಳು ಒಂದೇ ಬಣ್ಣವನ್ನು ಹೊಂದಿವೆ. ಘನವು ಒಂದು ಪ್ರಿಸಮ್ ನಿಂದ ದ್ವಿಮುಖಿ ಸಮಸೂತ್ರತೆಯು D_4h ಉಂಟಾಗುತ್ತದೆ, ಇದರಲ್ಲಿ ಎಲ್ಲ ನಾಲ್ಕು ಪಾರ್ಶ್ವಗಳು ಒಂದೇ ಬಣ್ಣವನ್ನು ಹೊಂದಿರುತ್ತವೆ. ಅತ್ಯಂತ ಕಡಿಮೆ ಸಮಸೂತ್ರತೆಯಾದ D_2h ಒಂದು ಪ್ರಿಸಮ್ ಸಮಸೂತ್ರತೆಯೂ ಸಹ ಆಗಿದೆ, ಇದರಲ್ಲಿ ಪಾರ್ಶ್ವಗಳು ಪರ್ಯಾಯ ಬಣ್ಣವನ್ನು ಹೊಂದಿರುತ್ತವೆ, ಈ ರೀತಿಯಾಗಿ ವಿರುದ್ಧ ಪಾರ್ಶ್ವಗಳ ಜೋಡಿಯಾಗಿ ಒಟ್ಟಾರೆಯಾಗಿ ಮೂರು ಬಣ್ಣಗಳನ್ನು ಹೊಂದಿರುತ್ತವೆ. ಪ್ರತಿಯೊಂದು ಸಮಸೂತ್ರತೆಯ ರೂಪವು ಒಂದು ವಿಭಿನ್ನ ವೈತೋಫ್ಫ್ ಸಂಕೇತವನ್ನು ಹೊಂದಿರುತ್ತವೆ.

ಹೆಸರು	ಸಾಮಾನ್ಯ ಷಣ್ಮುಖ	ಚತುಷ್ಕೋನದ ಪ್ರಿಸಮ್	ಘನಾಭ	ತ್ರಿಕೋನೀಯ ಟ್ರಾಪೆಜೊಹೆಡ್ರಾನ್
ಕೊಕ್ಸೆಟರ್-ಡಿನ್ಕಿನ್
ಶ್ಕಲಾಫ್ಲಿ ಸಂಕೇತ	{4,3}	{4}x{}	{}x{}x{}
ವೈತೋಫ್ಫ್ ಸಂಕೇತ	4 2	2	2 2 2
ಸಮಸೂತ್ರತೆ	Oh (*432)	D4h (*422)	D2h (*222)	D3d 2-3%
ಸಮಸೂತ್ರತೆಯ ಕ್ರಮ	24	16	8	12
ಇಮೇಜ್ (ಏಕಪ್ರಕಾರವಾಗಿ ಬಣ್ಣಹಚ್ಚುವುದು)	(111)	(112)	(123)

ಜ್ಯಾಮಿತೀಯ ನಿರೂಪಣೆಗಳು

ಈ ಪರಿಚಿತ ಆರು-ಮುಖದ ಚೌಕಳಿ ಒಟ್ಟು ಘನ-ರೂಪದಲ್ಲಿದೆ

ಪ್ಲೇಟಾನಿಕ್ ಕಾಯಗಳಲ್ಲಿ ಘನವು ಕ್ರಮಬದ್ಧವಾಗಿ ಟೈಲ್ ಮಾಡಲು ಸಾಧ್ಯವಾದ ಯೂಕ್ಲಿಡಿಯನ್ ಸ್ಪೇಸ್ ನ ಸಾಮರ್ಥ್ಯದೊಂದಿಗೆ ವಿಶಿಷ್ಟತೆಯನ್ನು ಹೊಂದಿದೆ. ಪಾರ್ಶ್ವಗಳ ಸಮತಲೀಯತೆಯನ್ನು ಹೊಂದಿರುವ ಪ್ಲೇಟಾನಿಕ್ ಕಾಯಗಳಲ್ಲಿಯೂ ಸಹ ಇದು ವಿಶಿಷ್ಟವಾಗಿದೆ, ಜೊತೆಗೆ ಈ ಕಾರಣದಿಂದ ಇದು ಒಂದು ಜೊನೊಹೆಡ್ರಾನ್ (ಪ್ರತಿಯೊಂದು ಪಾರ್ಶ್ವವು ಬಿಂದು ಸಮಸೂತ್ರತೆಯನ್ನು ಹೊಂದಿದೆ)ಗುಂಪಿನ ಏಕೈಕ ಭಾಗವಾಗಿದೆ.

ಒಂದು ಘನವನ್ನು 6 ಒಂದೇ ವಿಧವಾದ ಚತುಷ್ಕೋನದ ಪರಮಿಡ್ಗಳಾಗಿ ಭಾಗ ಮಾಡಬಹುದಾಗಿದೆ. ಈ ಚತುಷ್ಕೋನದ ಬಹುಭುಜಾಕೃತಿ(ಪಿರಮಿಡ್)ಗಳನ್ನು ಮತ್ತೊಂದು ಘನದ ಮುಖಗಳಿಗೆ ಸೇರಿಸಿದಾಗ, ಒಂದು ರಾಂಬಿಕ್ ದ್ವಾದಶಮುಖಿಯ ಸೃಷ್ಟಿಯಾಗುತ್ತದೆ.

ಇತರ ವಿಮಿತಿಗಳು

ನಾಲ್ಕು-ವಿಮಿತೀಯ ಯೂಕ್ಲಿಡಿಯನ್ ಸ್ಪೇಸ್ ನಲ್ಲಿ ಒಂದು ಘನದ ಸದೃಶಿಯವು ಒಂದು ವಿಶೇಷ ಹೆಸರನ್ನು ಹೊಂದಿದೆ- ಟೆಸ್ಸೆರಾಕ್ಟ್ ಅಥವಾ(ವಿರಳವಾಗಿ) ಹೈಪರ್ ಕ್ಯೂಬ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

n -ವಿಮಿತೀಯ ಯೂಕ್ಲಿಡಿಯನ್ ಸ್ಪೇಸ್ ನಲ್ಲಿ ಘನ ಸದೃಶಿಯವನ್ನು ಒಂದು ಹೈಪರ್ ಕ್ಯೂಬ್ ಅಥವಾ n -ವಿಮಿತೀಯ ಘನ ಅಥವಾ ಸರಳವಾಗಿ n -ಕ್ಯೂಬ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಇದು ಮೆಷರ್ ಪಾಲಿಟೋಪ್  ಎಂಬ ಹೆಸರಿನಿಂದಲೂ ಕರೆಯಲ್ಪಡುತ್ತದೆ.

ಕೆಳ ವಿಮಿತಿಗಳಲ್ಲೂ ಸಹ ಘನಕ್ಕೆ ಸದೃಶಿಯಗಳಿವೆ: 0 ವಿಮಿತಿಯಲ್ಲಿರುವ ಒಂದು ಬಿಂದು, ಒಂದು ವಿಮಿತಿಯಲ್ಲಿರುವ ಒಂದು ಖಂಡ ಹಾಗು ಒಂದು ಚತುಷ್ಕೋನದಲ್ಲಿರುವ ದ್ವಿವಿಮಿತೀಯಗಳು.

ಸಂಬಂಧಿತ ಬಹುಮುಖಿಗಳು

ಒಂದು ಘನದ ಬಹುಭುಜಗಳನ್ನು ನಾಲ್ಕರ ಎರಡು ಗುಂಪುಗಳಾಗಿ ವಿಂಗಡಿಸಬಹುದು, ಇದರಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಒಂದು ಸಾಮಾನ್ಯ ಟೆಟ್ರಹೆಡ್ರನ್(ನಾಲ್ಕು ಪಕ್ಕಗಳಿರುವ ಘನ)ನ್ನು ರೂಪಿಸುತ್ತದೆ; ಸಾಧಾರಣವಾಗಿ ಇದನ್ನು ಡೆಮಿಕ್ಯೂಬ್ ಎಂಬ ಹೆಸರಿನಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಇವೆರಡೂ ಒಟ್ಟಾರೆಯಾಗಿ ಒಂದು ಸಾಮಾನ್ಯ ಸಂಯುಕ್ತವನ್ನು ರೂಪಿಸುತ್ತದೆ, ಸ್ಟೆಲ್ಲಾ ಆಕ್ಟಾಂಗುಲ. ಈ ಎರಡೂ ರೂಪಗಳ ಛೇದನವು ಒಂದು ಸಾಮಾನ್ಯ ಅಷ್ಟಮುಖಿಯನ್ನು ರೂಪಿಸುತ್ತದೆ. ಒಂದು ಸಾಧಾರಣ ಟೆಟ್ರಹೆಡ್ರನ್ ನ ಸಮಸೂತ್ರತೆಗಳು ಘನಕ್ಕೆ ಹೊಂದಾಣಿಕೆಯಾಗುವುದರ ಜೊತೆಗೆ ತನ್ನಷ್ಟಕ್ಕೆ ಟೆಟ್ರಹೆಡ್ರನ್ ನ ರಚನೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ; ಘನದ ಇತರ ಬಹುಮುಖಿಗಳು ಪರಸ್ಪರ ಎರಡರ ನಕ್ಷೆಯನ್ನು ರೂಪಿಸುತ್ತದೆ.

ಅಂತಹ ಒಂದು ಸಾಧಾರಣ ಟೆಟ್ರಹೆಡ್ರನ್, ಒಂದು ಘನದ ⅓ರಷ್ಟು ಘನ ಅಳತೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಉಳಿದ ಕ್ಷೇತ್ರವು ನಾಲ್ಕು ಸಮನಾದ ಅಸಮರೂಪದ ಟೆಟ್ರಹೆಡ್ರನ್ ನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ಇದರಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಒಂದು ಘನದ 1/6ರಷ್ಟು ಘನ ಅಳತೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ.

ಒಂದು ನೀಳಕಲನಿಸಿದ ಘನವೇ ಕ್ಯೂಬೋಕ್ಟಹೆಡ್ರನ್. ಸಣ್ಣ ಅಂಚುಗಳನ್ನು ತೆಗೆದುಹಾಕಿದಾಗ ನಮಗೆ 6 ಅಷ್ಟಮುಖಿ ಪಾರ್ಶ್ವಗಳ ಹಾಗು 8 ತ್ರಿಕೋಣ ಪಾರ್ಶ್ವಗಳ ಒಂದು ಬಹುಮುಖಿಯು ಲಭ್ಯವಾಗುತ್ತದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳಬಹುದಾದರೆ ನಮಗೆ ಸಾಮಾನ್ಯ ಅಷ್ಟಮುಖಿಗಳು ಲಭ್ಯವಾಗುತ್ತದೆ (ಮೊಟಕುಗೊಂಡ ಘನ). ಒಂದು ಸರಿಯಾದ ಪ್ರಮಾಣದಲ್ಲಿ ಕೋನಗಳು ಹಾಗು ಅಂಚುಗಳನ್ನು ತೆಗೆದುಹಾಕಿದಾಗ ರಾಂಬಿಕ್ಯೂಬೋಕ್ಟಹೆಡ್ರನ್ ಲಭ್ಯವಾಗುತ್ತದೆ.

ಒಂದು ಘನವನ್ನು ಒಂದು ದ್ವಾದಶಮುಖಿಯಲ್ಲಿ ಒಳರಚನೆ ಮಾಡಬಹುದಾಗಿದೆ, ಈ ರೀತಿಯಾಗಿ ಘನದ ಪ್ರತಿ ಬಹುಭುಜವು ದ್ವಾದಶಮುಖಿಯ ಬಹುಭುಜವಾಗಿರುವುದರ ಜೊತೆಗೆ ಪ್ರತಿ ಅಂಚುಗಳು ದ್ವಾದಶಮುಖಿಯ ಪಾರ್ಶ್ವಗಳಲ್ಲಿ ಒಂದಕ್ಕೆ ಕರ್ಣೀಯವಾಗಿರುತ್ತದೆ; ಇಂತಹ ಎಲ್ಲ ಘನಗಳನ್ನು ಸೇರಿಸಿದಾಗ ಐದು ಘನಗಳ ಸಾಮಾನ್ಯ ಸಂಯೋಜನೆಯು ಸೃಷ್ಟಿಯಾಗುತ್ತದೆ.

ಒಂದು ಘನಕ್ಕೆ ನೇರವಾಗಿ ಸಂಪರ್ಕ ಹೊಂದಿದ ಅದರ ಎರಡು ವಿರುದ್ಧ ಮೂಲೆಗಳನ್ನು 3 ಬಹುಭುಜೀಯ ಅಳತೆಗೆ ಮೊಟಕುಗೊಳಿಸಿದಾಗ, ಒಂದು ಅಸಮರೂಪದ ಅಷ್ಟಮುಖಿಯು ರೂಪುಗೊಳ್ಳುತ್ತದೆ. ಇಂತಹ ಅಸಮರೂಪದ ಎಂಟು ಅಷ್ಟಮುಖಿಶ್ರ(ಆಕ್ಟಾಹೆಡ್ರಾ)ಗಳನ್ನು ಒಂದು ಸಾಮಾನ್ಯ ಅಷ್ಟಮುಖಿಯ ತ್ರಿಕೋನೀಯ ಪಾರ್ಶ್ವಗಳಿಗೆ ಸೇರಿಸಿ ಕ್ಯೂಬೋಕ್ಟಹೆಡ್ರನ್ ನ್ನು ರೂಪಿಸಬಹುದು.

• 
  ಕ್ಯೂಬ್(ಘನ)ನಲ್ಲಿರುವ ಎರಡು ಟೆಟ್ರಹೆಡ್ರನ್ (ಸ್ಟೆಲ್ಲಾ ಆಕ್ಟ್ಯಾಂಗುಲ)
• 
  ಸರಿಪಡಿಸಲಾದಂತಹ ಘನ (ಕ್ಯೂಬೋಕ್ಟಹೆಡ್ರನ್)
• 
  ಮೊಟಕುಗೊಳಿಸಿದ ಘನ
• 
  ಕ್ಯಾನ್ಟೆಲ್ಲೆಟೆಡ್ ಘನ(ರಾಂಬಿಕ್ಯೂಬೋಕ್ಟಹೆಡ್ರನ್)
• 
  ಎಲ್ಲಭಾಗದಲ್ಲೂ ಮೊಟಕುಗೊಂಡ ಘನ(ಮೊಟಕುಗೊಂಡ ಕ್ಯೂಬೋಕ್ಟಹೆಡ್ರನ್)
• 
  ಗಿಡ್ಡವಾದ ಘನ
• 
  ಮೂರು ಘನಗಳ ಸಂಯೋಗ
• 
  ಒಂದು ಪರ್ಯಾಯವಾಗಿ ಮೊಟಕುಗೊಂಡ ಘನ

ಮೇಲೆ ತೋರಿಸಲ್ಪಟ್ಟ ಎಲ್ಲ ಚಿತ್ರಗಳು ವಿಶೇಷವಾಗಿ ಕಡೆಯದು ಘನದಂತೆ ಒಂದೇ ಸಮಸೂತ್ರತೆಗಳನ್ನು ಹೊಂದಿದೆ (ನೋಡಿ ಆಕ್ಟಹೆಡ್ರಲ್ ಸಿಮೆಟ್ರಿ(ಅಷ್ಟಮುಖೀಯ ಸಮಸೂತ್ರತೆ)

ಹೆಮಿಕ್ಯೂಬ್ ಘನದ 2-ರಿಂದ-1 ರ ಭಾಗಲಬ್ದವಾಗಿದೆ.

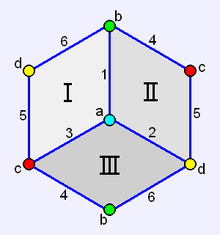
ಪೂರ್ಣವಿರುದ್ಧ ನಕ್ಷೆಯ ಪರಿಣಾಮವಾಗಿ ಉಂಟಾದ ಘನದ ಭಾಗಲಬ್ದವು ಒಂದು ಪ್ರಕ್ಷೇಪಿತ ಬಹುಮುಖಿ, ಹೆಮಿಕ್ಯೂಬ್ ನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ.

ಸಾಮಾನ್ಯ ಬಹುಮುಖಿಗಳ ಹಲವಾರು ವರ್ಗಗಳಲ್ಲಿ ಘನವು ಒಂದು ವಿಶೇಷ ಮಾದರಿಯಾಗಿದೆ:

ಹೆಸರು	ಸಮಾನಾಂತರವಾದ ತುದಿ-ಉದ್ದಗಳು?	ಸಮಾನಾಂತರ ಕೋನಗಳು?	ಲಂಬ ಕೋನಗಳು?
ಘನ	ಹೌದು	ಹೌದು	ಹೌದು
ರಾಂಬೋಮುಖಿ	ಹೌದು	ಹೌದು	ಇಲ್ಲ
ಘನಭ	ಇಲ್ಲ	ಹೌದು	ಹೌದು
ಸಮಾಂತರುಪರಿಪದಿ	ಇಲ್ಲ	ಹೌದು	ಇಲ್ಲ
ಚತುಷ್ಕೋನೀಯ ಮುಖದ ಷಣ್ಮುಖ	ಇಲ್ಲ	ಇಲ್ಲ	ಇಲ್ಲ

ಸಂಚಯಾತ್ಮಕ ಘನಗಳು

ಘನದ ಒಂದು ಭಿನ್ನ ಮಾದರಿಯೆಂದರೆ ಕ್ಯೂಬ್ ಗ್ರಾಫ್ (ಘನ ರೇಖಾನಕ್ಷೆ), ಇದು ಜ್ಯಾಮಿತೀಯ ಘನದ ಬಹುಮುಖಿಗಳು ಹಾಗು ಅಂಚುಗಳ ರೇಖಾನಕ್ಷೆ. ಇದು ಹೈಪರ್ ಕ್ಯೂಬ್ ರೇಖಾನಕ್ಷೆಯ ಒಂದು ವಿಶೇಷ ಮಾದರಿ.

ಇದರ ಒಂದು ವಿಸ್ತೀರ್ಣವೇ 3-ವಿಮಿತೀಯ k -ary ಹಮ್ಮಿಂಗ್ ರೇಖಾನಕ್ಷೆ, ಇದರಲ್ಲಿ k = 2 ಎಂಬುದು ಘನ ರೇಖಾನಕ್ಷೆ. ಈ ಮಾದರಿಯ ರೇಖಾನಕ್ಷೆಗಳು ಕಂಪ್ಯೂಟರ್ ನ ಪ್ಯಾರಲೆಲ್ ಪ್ರಾಸೆಸ್ಸಿಂಗ್ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ.

ಇವನ್ನೂ ನೋಡಿ

• ಏಕಮಾನದ ಘನ
• ಟೆಸ್ಸೆರಾಕ್ಟ್
• ಘನ(ಚಿತ್ರ)
• ಟ್ರಪೆಜೊಹೆಡ್ರಾನ್
• ಯೋಶಿಮೋಟೋ ಘನ
• ದಿ ಕ್ಯೂಬ್ (ಗೇಮ್ ಷೋ)
• ಪ್ರಿನ್ಸ್ ರೂಪರ್ಟ್ ನ ಘನ
• OLAP ಘನ

ಆಕರಗಳು

1. • Weisstein, Eric W., "Cube", MathWorld.

ಬಾಹ್ಯಕೊಂಡಿಗಳು

Listen to this article (info/dl)

noicon

noicon

Spoken Wikipedia

This audio file was created from a revision of the "ಘನ (ಆಕೃತಿ)" article dated 2006-07-07, and does not reflect subsequent edits to the article. (Audio help)

More spoken articles

• ಕ್ಯೂಬ್: ಇಂಟರಾಕ್ಟಿವ್ ಪಾಲಿಹೆಡ್ರನ್ ಮಾಡೆಲ್ Archived 2007-10-09 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
• K.J.M. ಮ್ಯಾಕ್ಲೆಯನ್, ಏ ಜಿಆಮಿಟ್ರಿ ಅನಾಲಿಸಿಸ್ ಆಫ್ ದಿ ಫೈವ್ ಪ್ಲಟೋನಿಕ್ ಸಾಲಿಡ್ಸ್ ಅಂಡ್ ಅದರ್ ಸೆಮಿ-ರೆಗ್ಯೂಲರ್ ಪಾಲಿಹೆಡ್ರ
• ದಿ ಯೂನಿಫಾರ್ಮ್ ಪಾಲಿಹೆಡ್ರ
• ವರ್ಟ್ಯೂಅಲ್ ರಿಯಾಲಿಟಿ ಪಾಲಿಹೆಡ್ರ
• ವಾಲ್ಯೂಮ್ ಆಫ್ ಏ ಕ್ಯೂಬ್, ವಿಥ್ ಇಂಟರಾಕ್ಟಿವ್ ಅನಿಮೇಶನ್

ಟೆಂಪ್ಲೇಟು:Uniform polyhedra navigator