Пи (сан)

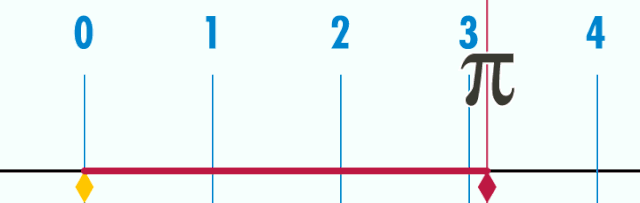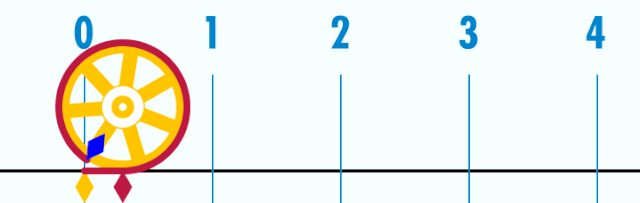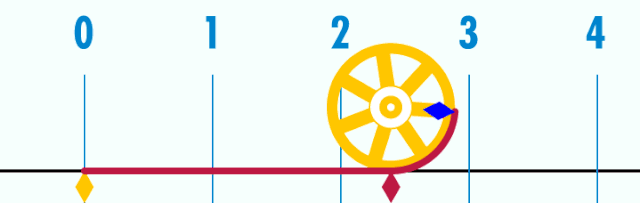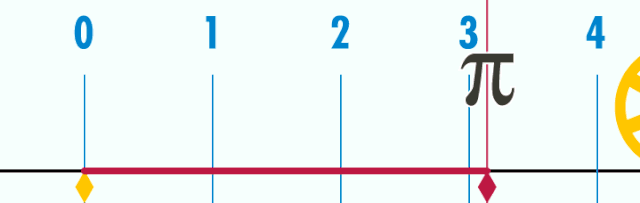
${\displaystyle \pi }$ саны («пи» деп оқылады) — шеңбер ұзындығының оның диаметріне қатынасын сипаттайтын математикалық тұрақты шама. Юнан әліппесінің алғашқы әрпімен - «пи » белгіленеді. 2022 жылдың маусымына «пи» санының үтірден кейінгі 100 триллион таңбасы табылды.

Егер шеңбер диаметрі бірге тең деп алынса, шеңбер ұзындығы — «пи» санына тең болады.

Қасиеттері

Иррационалдық және Трансценденттік

"Пи" саны иррационал, яғни оның мәні m / n бөлшек түрінле нақты көрсетілмейді, m - бүтін сан ал n - натурал сан. Демек оның ондық бөлігі шексіз және де периодты емес. "Пи" санының иррационалдығын бірінші рет 1761 жылы Иоганн Ламберт ғалымы

тангенстың үздіксіз бөлшек ретінде бөлшектеу арқылы дәлелдеді. "Пи" және "Пи²" санының иррационалдығын 1794 жылы Лежандр ғалымы қатаң дәлелдеді. Кейбір дәлелдеулер Иррационалдық дәлелдеу мақаласында шағын келтірілген

"Пи" трансцедентті сан, яғни ол коэффиценті бүтін сан көпмүшенің түбірі бола алмайды. "Пи" санының трансцеденттілігін алғаш рет 1882 жылы Кёнигсберкг университетінің профессорымен, ал одан кейін Мюнхен университетінің профессорымен дәлелденді. Осы дәлелдеуді 1894 жылы Феликс Клейн ықшамдады. Евклид геометриясында дөнгелек ауданы мен шенбер ұзындығы "пи" санының функциялары болып табылатындықтан, "пи" санының трансцендеттігі 2500 жылдан астам дөнгелек квадратурасын салуға арналған есептің нүктесін қойды.

"e константасының "пи" дәрежесін" трансценденттігін 1934 жылы Гельфонд ғалымы дәлелдеді.1996 жылы Юрий Нестеренко дәлелдеуі бойынша, әрбір n - натурал санына "пи" және де "e константасының пи көбейтілген түбір астындағы n дәрежесі" өзара алгебралық тұрғыда тәуелсіз., осыдан "пи" + "е константасынын пи дәрежесінде ", "пи көбейтілген е константасы, осының пи дәрежесі және е константасының пи көбейтілген түбір астында n дәрежесі" осы сандар трансцендентті болып келеді.

"Пи" периодты сақина элементтердің тобына жатады, яғни есептеле алатын және арифметикалық сан. Бірақ "1 / пи" периодты сақина тобына жататына белгісіз.

Тарихы

Пи саны — шеңбер ұзындығының оның диаметріне қатынасын көрсететін және математикада белгілі бір иррационал санды белгілеу үшін қолданылатын грек әрпі. Бұл белгілеуді алғаш рет 1706 ж. ағылшын математигі У.Джонс (1675 — 1749) пайдаланғанымен, жаппай қолданысқа 1736 ж. Л.Эйлердің (1707 — 83) еңбегінен кейін ғана ене бастады. Кез келген иррационал сандар сияқты Пи саны да шектеусіз периодты емес ондық бөлшек түрінде жазылады: ${\displaystyle \pi }$=3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 …

Ерте замандардан бастап дөңгелек пен шеңберге қатысты практик. есептеулер рационал сандардың көмегімен ${\displaystyle \pi }$-дің жуық мәнін іздеудің қажеттілігін туғызды. Ежелгі Египетте (б.з.б. 2-мыңжылдықта) дөңгелек ауданын есептеу кезінде ${\displaystyle \pi }$-дің шамамен 3-ке тең мәні немесе дәлірек тең мәні қолданылған. Архимед (б.з.б. 3 ғ.) іштей және сырттай сызылған көпбұрышы бар шеңберлерді салыстыра отырып, ${\displaystyle \pi }$-дің дәл мәні және сандарының аралығында екенін тапқан (бұл жуықтаулар қазіргі кезде де үлкен дәлдікті қажет етпейтін есептеулерде қолданылып келеді). 5 ғасырдың 2-жартысында қытай математигі Цзу Чун-чжи ${\displaystyle \pi }$-дің 3,1415927-ге тең жуық мәнін тапқан, бұл мән ұзақ уақыттан кейін Еуропада да табылды (16 ғасырда); бұл жуықтаудың тек 7-ондық таңбасында ғана қателік бар. ${\displaystyle \pi }$-дің дәлірек жуық мәнін табу жұмыстары жалғасып, Ғийас әд-Дин ибн Масуд Жәмшид әл-Кәши Пи санының 17 ондық таңбасын, ал голланд математигі Лудольф ван Цейлен (1540 — 1610) 32 ондық таңбасын тапқан. 1962 ж. Пи санының жүз мың ондық таңбасы электрондық есептеуіш машинаның көмегімен табылды. Пи саны түрлі геометриялық есептеулермен қатар, арифметикалық тізбектердің шегін табуда, Эйлер формуласында, т.б. кездеседі.

18 ғасырдың аяғында И.Ламберт (1728 — 77) пен А.Лежандр (1752 — 1833) ${\displaystyle \pi }$-дің иррационал сан екенін айтса, 1882 ж. Ф.Линдеман (1852 — 1939) трансцендент сан екенін дәлелдеген.^[1]

Есептеу, бағалау

• ${\displaystyle {\frac {22}{7}}}$ (Архимед),
• ${\displaystyle {\frac {377}{120}}}$ (үндіс ойшылы мен астрономы Арьябхаттың кітабында 5-ші ғасырда берілген),
• ${\displaystyle {\frac {355}{113}}}$ (Арьябхат замандасы көнеқытайлық Цзу Чун-цжи астрономы бағалаған-мыс).

• үтірден кейін 510 белгісі:

  π ≈ 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362…

• Үтірден кейін жүз миллион белгісі
  • 3.141592653589793238462643383279502884197169399375105820974944592.jp

Лудольф саны

Лудольф саны - ${\displaystyle ~\pi }$ (пи) санының 32 таңбалы ондық белгілермен өрнектелген жуық мәні. Бұл мәнді нидерланд математигі Ван Цейлен Лудольф (1540-1610) есептеп тапқан. Бұл 1615 жылы (ғалым қайтыс болған соң) жарияланған.

• ${\displaystyle ~\pi =3,14159265358979323846264338327950.}$

• π = 3,141 592 653 589 793 238 462 643 383 279 50^[2]

Дереккөздер

1. «Қазақстан»: Ұлттық энцклопедия / Бас редактор Ә. Нысанбаев – Алматы «Қазақ энциклопедиясы» Бас редакциясы, 1998 ISBN 5-89800-123-9, VII том
2. "Математикалық ойашар", "Қазақ энциклопедиясы" Алматы, 2009 ISBN 9965-893-25-X

Ортаққорда бұған қатысты медиа санаты бар: Pi