分布定数回路

分布定数回路（ぶんぷじょうすうかいろ、ぶんぷていすうかいろ）は電気回路の一種で、回路素子が有限の個数で集中することなく無限に分布している回路、そのようなモデルで表現される回路である。

ケーブルのように一様な形状・電気特性の箇所にケーブルの長さよりも十分に波長が短くなるような高周波の交流信号が加えられ、ケーブルの全体にわたって電圧・電流分布が均一であるとみなせないような状況の下での振る舞いを取り扱う。対義の概念は集中定数回路（しゅうちゅうじょうすうかいろ）である。

特性を表すためにSパラメータを用いることが多い。

概要

典型的な例として平行二線線路、同軸ケーブルを考えてみる。 長さ方向に導通を前提とした小さい抵抗成分、誘導成分が、長さ方向のある点では導体間に容量成分、絶縁を前提とした大きい抵抗成分が存在する。

直流または十分に低い周波数では、線路を構成する導体全体で電圧・電流分布は一様と扱うことができる。

周波数が高い領域では、誘導成分、容量成分の影響が顕在化し、印加した信号の線路上での進行をモデル化した電信方程式で取り扱う必要がある。

分布定数線路は周波数が高い領域での電気回路の取り扱いである。 ここでいう周波数が高いとは、信号の周波数と回路の寸法的大きさから相対的に決まるもので、一般にはサイズがλ/4程度になる程度から分布定数回路的な取り扱いの必要がある。 すなわち、周波数50Hz/60Hzの商用電源の送電網のように、電気回路一般としては低周波として扱われる周波数の電圧・電流を扱う場合であっても、その線路長が㎞単位の長さで回路全体に亘って電圧・電流が一定と見なせない場合には、分布定数回路として扱う必要がある。

低周波回路では周波数フィルタをつくるのに個別素子としての誘導素子インダクタンス(＝コイル)・容量素子キャパシタ(＝コンデンサ)・抵抗素子抵抗を用いるが、超高周波回路では配線自体の誘導性・容量性・抵抗性が顕在化するため、配線だけでフィルタ(LPF・BPF・HPF・BEF)を構成することができる。

設計には始めに、配線の特性を考慮して、信号の伝播に位相遅れが生じることを念頭に伝播速度・反射係数・減衰率・周波数余裕などを設定する必要がある。 配線間の容量・信号透過率も考慮しなければならないため非常に高度な設計法を必要とする。

回路方程式と諸特性

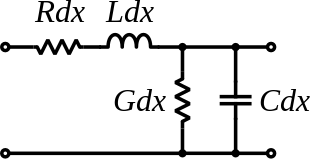
伝送線路の基本の構成要素の略図

伝送線路の回路モデルを示す。

R:単位長さあたりの抵抗成分

L：単位長さあたりのインダクタンス成分

G：単位長さあたりの導体間のコンダクタンス成分

C：単位長さあたりの導体間の容量成分

である。

分布定数線路の基本方程式

図で示される部分の電圧・電流分布についての関係を示す以下の2式は分布定数回路における基本方程式である。

${\displaystyle -{\frac {\partial }{\partial x}}V(x,t)=L{\frac {\partial }{\partial t}}I(x,t)+RI(x,t)}$

${\displaystyle -{\frac {\partial }{\partial x}}I(x,t)=C{\frac {\partial }{\partial t}}V(x,t)+GV(x,t)}$

さらにxで偏微分して

${\displaystyle {\frac {\partial ^{2}}{{\partial x}^{2}}}V=LC{\frac {\partial ^{2}}{{\partial t}^{2}}}V+(RC+GL){\frac {\partial }{\partial t}}V+GRV}$

${\displaystyle {\frac {\partial ^{2}}{{\partial x}^{2}}}I=LC{\frac {\partial ^{2}}{{\partial t}^{2}}}I+(RC+GL){\frac {\partial }{\partial t}}I+GRI}$

を得る。これは「電信方程式（Telegrapher's equations, Telegraphers equations）」と呼ばれる。

さらに上式に ${\displaystyle e^{j\omega t}}$ なる電源を印加した時の偏微分方程式の定常解（特殊解）は伝播定数${\displaystyle \gamma }$、特性インピーダンス${\displaystyle Z_{0}}$を導入して

${\displaystyle V=K_{1}e^{-\gamma x}+K_{2}e^{\gamma x}}$

${\displaystyle I={\frac {1}{Z_{0}}}(K_{1}e^{-\gamma x}-K_{2}e^{\gamma x})}$

となる。${\displaystyle K_{1}}$と${\displaystyle K_{2}}$は境界条件によって決まる定数である。

伝播定数${\displaystyle \gamma }$、特性インピーダンス${\displaystyle Z_{0}}$は、

${\displaystyle \gamma ={\sqrt {(R+j\omega L)(G+j\omega C)}}}$

${\displaystyle Z_{0}={\sqrt {\frac {R+j\omega L}{G+j\omega C}}}}$

である。さらに、伝播定数${\displaystyle \gamma }$の実部である減衰定数${\displaystyle \alpha }$および、虚部である位相定数${\displaystyle \beta }$は、以下のようになる。

${\displaystyle \gamma =\alpha +j\beta ={\sqrt {ZY}}={\sqrt {(R+j\omega L)(G+j\omega C)}}}$

${\displaystyle \alpha ={\sqrt {{\frac {1}{2}}\left({\sqrt {(R^{2}+\omega ^{2}L^{2})(G^{2}+\omega ^{2}C^{2})}}+(RG-\omega ^{2}LC)\right)}}}$

${\displaystyle \beta ={\sqrt {{\frac {1}{2}}\left({\sqrt {(R^{2}+\omega ^{2}L^{2})(G^{2}+\omega ^{2}C^{2})}}-(RG-\omega ^{2}LC)\right)}}}$

そして、特性インピーダンス${\displaystyle Z_{0}}$の実部${\displaystyle R_{0}}$と虚部${\displaystyle X_{0}}$を求めると以下のようになる。

${\displaystyle Z_{0}={\sqrt {\frac {R+j\omega L}{G+j\omega C}}}=R_{0}+jX_{0}}$

${\displaystyle R_{0}={\sqrt {{\frac {1}{2}}\left({\sqrt {\frac {R^{2}+\omega ^{2}L^{2}}{G^{2}+\omega ^{2}C^{2}}}}+{\frac {RG+\omega ^{2}LC}{G^{2}+\omega ^{2}C^{2}}}\right)}}}$

${\displaystyle X_{0}={\sqrt {{\frac {1}{2}}\left({\sqrt {\frac {R^{2}+\omega ^{2}L^{2}}{G^{2}+\omega ^{2}C^{2}}}}-{\frac {RG+\omega ^{2}LC}{G^{2}+\omega ^{2}C^{2}}}\right)}}}$

無損失線路

伝送線路に損失がない場合、${\displaystyle R=G=0}$であり、

${\displaystyle Z_{0}={\sqrt {\frac {L}{C}}}}$

${\displaystyle \gamma =\alpha +j\beta ={\sqrt {(j\omega L)(j\omega C)}}=j\omega {\sqrt {LC}}}$

となる。

無ひずみ線路

伝送線路において以下の無ひずみ条件

${\displaystyle {\frac {R}{L}}={\frac {G}{C}}}$

つまり、

${\displaystyle RC=LG}$

を満たすとき、

${\displaystyle \alpha ={\sqrt {RG}}}$
${\displaystyle \beta =\omega {\sqrt {LC}}}$

となる。

反射現象

分布定数回路において、伝送線路の特性インピーダンスと伝送線路の終端のインピーダンスが異なるなど、「入射波」に対する「反射波」が存在するとき、位置xにおける反射係数${\displaystyle \rho _{x}}$は、電圧の場合、入射波を${\displaystyle V_{i(x)}}$、反射波を${\displaystyle V_{r(x)}}$とすると、

${\displaystyle \rho _{(x)}={\frac {V_{r(x)}}{V_{i(x)}}}={\frac {K_{2}e^{\gamma x}}{K_{1}e^{-\gamma x}}}={\frac {Z_{x}-Z_{0}}{Z_{x}+Z_{0}}}}$

となる。

特に、伝送線路の終端（${\displaystyle x=l}$）における電圧の反射係数は

${\displaystyle \rho _{(l)}={\frac {V_{r(l)}}{V_{i(l)}}}={\frac {K_{2}e^{\gamma l}}{K_{1}e^{-\gamma l}}}={\frac {Z_{l}-Z_{0}}{Z_{l}+Z_{0}}}}$

である。

このとき、伝送路の終端が開放（open）のとき、すなわち${\displaystyle Z_{l}=\infty }$の場合、${\displaystyle \rho _{(l)}=1}$である。（完全反射）

また、伝送路の終端が短絡（short）のとき、すなわち${\displaystyle Z_{l}=0}$の場合、${\displaystyle \rho _{(l)}=-1}$である。（完全反射）

さらに、伝送路の終端が${\displaystyle Z_{0}}$で終端のとき、すなわち${\displaystyle Z_{l}=Z_{0}}$の場合、${\displaystyle \rho _{(l)}=0}$である。（インピーダンス整合、反射波なし）

透過現象

伝送線路のインピーダンスが変化する点などにおいて、反射と透過の現象が起きる。入射してきた波が異なるインピーダンスの伝送線路に透過する波を「透過波」という。

電圧の入射波を${\displaystyle V_{i}}$、反射波を${\displaystyle V_{r}}$、透過波を${\displaystyle V_{t}}$、電流の入射波を${\displaystyle I_{i}}$、反射波を${\displaystyle I_{r}}$、透過波を${\displaystyle I_{t}}$とするとき、以下の関係が成り立つ。

${\displaystyle V_{t}=V_{i}+V_{r}}$
${\displaystyle I_{t}=I_{i}-I_{r}}$

また、透過波と入射波の比を、それぞれ電圧透過係数、電流透過係数という。

電圧透過係数は以下である。

${\displaystyle {\frac {V_{t}}{V_{i}}}={\frac {V_{i}+V_{r}}{V_{i}}}=(1+\rho )}$

電流透過係数は以下である。

${\displaystyle {\frac {I_{t}}{I_{i}}}={\frac {I_{i}-I_{r}}{I_{i}}}=(1-\rho )}$

定在波

伝送線路に電源をおいて奨励波を発生させ、伝送線路上に入射波と反射波の両方の波が存在するとき、2つの波は互いに干渉しあって合成が起き、伝送線路上には時間に無関係で位置に固有な波ができ、これを「定在波」という。

また、電圧の振幅の最大値と最小値の比を「定在波比」（または「電圧定在波比」）という。定在波比${\displaystyle \sigma }$は以下で定義される。

${\displaystyle \sigma ={\frac {|V_{max}|}{|V_{min}|}}={\frac {1+|\rho |}{1-|\rho |}}}$

${\displaystyle |\rho |}$はl点における反射係数。

関連項目

• アナログ回路
• 高周波回路
• スタブ
• CPU
• 定在波 - 定在波比
• スミスチャート

外部リンク

• 1.分布定数回路とは何か