ユークリッドの互除法

ユークリッドの互除法（ユークリッドのごじょほう、英: Euclidean Algorithm）は、2 つの自然数の最大公約数を求める手法の一つである。

252と105のためのユークリッドの互除法のアニメーション。
クロスバーは、最大公約数（GCD）である21の倍数を表す。
それぞれのステップにおいて、1つの番号がゼロになるまで、より少ない数はより大きな数から引かれる。
残りの数は、GCD。

2 つの自然数 a, b (a ≧ b) について、a の b による剰余を r とすると、 a と b との最大公約数は b と r との最大公約数に等しいという性質が成り立つ。この性質を利用して、 b を r で割った剰余、 除数 r をその剰余で割った剰余、と剰余を求める計算を逐次繰り返すと、剰余が 0 になった時の除数が a と b との最大公約数となる。

明示的に記述された最古のアルゴリズムとしても知られ、紀元前300年頃に記されたユークリッドの『原論』第 7 巻、命題 1 から 3 がそれである^{[注釈 1]}。

例

(問題) 1071 と 1029 の最大公約数を求める。

• 1071 を 1029 で割った余りは 42
• 1029 を 42 で割った余りは 21
• 42 を 21 で割った余りは 0

よって、最大公約数は21である。

証明

a, b は自然数で a ≠ 0 とする。 b を a で割った商を q、剰余を r とすると

b = qa + r

今、d₀ を a と r の両方を割り切る自然数とする。

このとき d₀ は積 qa を割り切るから、和 qa + r も割り切るが、qa + r は b に等しい。したがって、d₀ は a とb を割り切る。すなわち a と r の公約数はすべてb と aの公約数である。

逆に、d₁ を b と a の両方を割り切る自然数とする。

d₁ は qa を割り切るから差 b - qa を割り切るが、b - qa は r に等しい。したがって、d₁ は a とrを割り切る。言い換えると b と a の公約数はすべてa と r の公約数である。

したがって、b と a の公約数全体の集合は a と r の公約数全体の集合に等しく、特に b と a の最大公約数は a と r の最大公約数でなければならない。

手続き的記述

ユークリッドの互除法の仕組みは、この図のように最大公約数を求める対象の２つの整数を幅と高さに設定した長方形内での赤色の斜めの直線の描画過程によっても表現できる。 赤色の斜めの直線の描画は、はじめはその長方形内を描画範囲とし、その角から内部に向け、かつ、その辺に対して45度の差を持たせて開始する。 描画範囲の辺の途中に当たれば、その内部へ直角反射するように角度を変える。 赤色の斜めの直線が反射後に描画範囲の向かいの辺と異なる辺の途中に当たる場合、描画範囲の長辺の長さを短辺の長さで割ると余りが生じる状態となっており、直前の反射地点を足掛かりに描画範囲を垂直に区切ってその範囲を絞りこむ。 （区切られて出来た小さいほうの範囲を以後の描画範囲とする） （除数および被除数の変更に相当） 赤色の斜めの直線が描画範囲の角に到達した場合、描画範囲の長辺の長さを短辺の長さで余りなく割れる状態となっており、描画の終了となり、最後にして最小の描画範囲の短辺の長さが最大公約数となる。

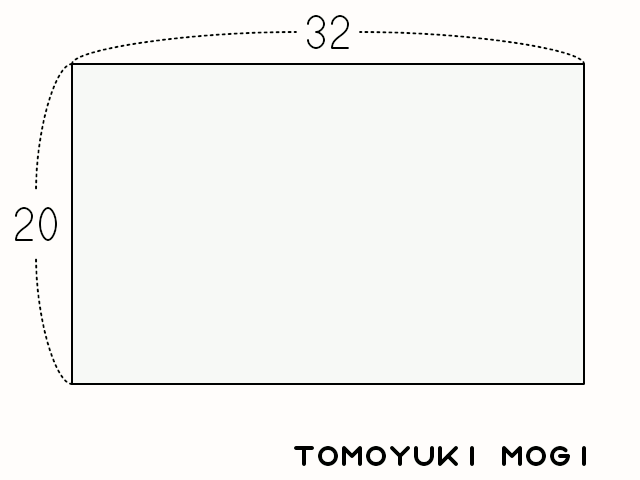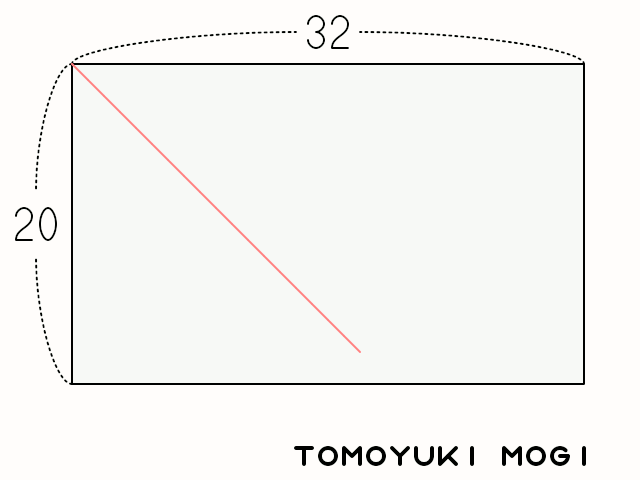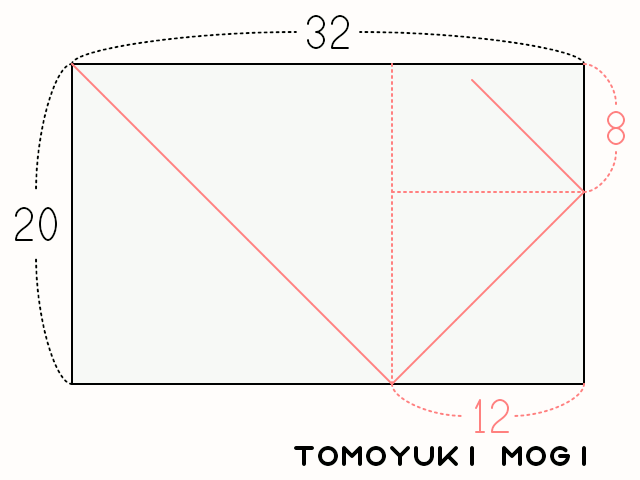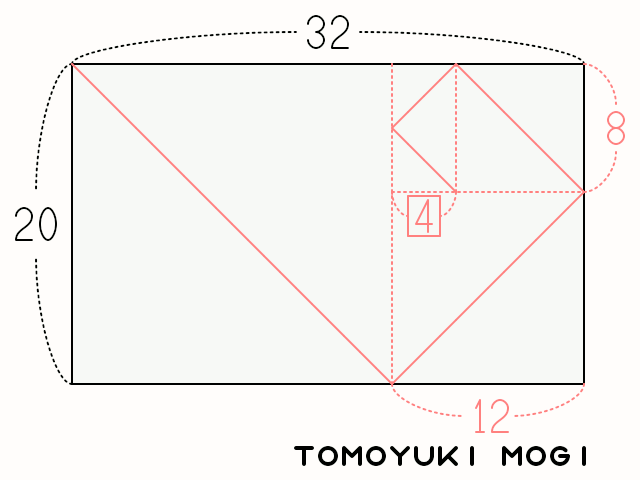
手続き的に記述すると、次のようになる。

1. 入力を m, n (m ≧ n) とする。
2. n = 0 なら、 m を出力してアルゴリズムを終了する。
3. m を n で割った余りを新たに n とし、更に 元のnを新たにm とし 2. に戻る。

上記の手順は「n, m に対して剰余の演算を行うことができる」という仮定だけに依っているので、整数環だけではなく任意のユークリッド整域においても同様にして最大公約因子を求めることができる。

拡張された互除法

整数 m, n の最大公約数 (英: Greatest Common Divisor) を gcd(m,n) と表すときに、（拡張された）ユークリッドの互除法を用いて、mx + ny = gcd(m, n) の解となる整数 x, y の組を見つけることができる。上の例の場合、m = 1071, n = 1029 のとき、

1071 = 1 × 1029 + 42

1029 = 24 × 42 + 21

42 = 2 × 21

であるから、gcd(1071, 1029) = 21 であり、

21 = 1029 − 24 × 42 

= 1029 − 24 × (1071 − 1 × 1029)

= −24 × 1071 + 25 × 1029

となるので、x = −24, y = 25 である。

特に、m, n が互いに素（最大公約数が 1）である場合、mx + ny = 1 の整数解を (x, y) とすると、mx + ny = c は任意の整数 c に対して整数解 (cx, cy) をもつことが分かる。

一般に、${\displaystyle m=r_{0},n=r_{1}}$ において、ユークリッドの互除法の各過程を繰り返して

${\displaystyle r_{0}=k_{0}r_{1}+r_{2}\ \ (0<r_{2}<r_{1})}$

${\displaystyle r_{1}=k_{1}r_{2}+r_{3}\ \ (0<r_{3}<r_{2})}$

${\displaystyle r_{2}=k_{2}r_{3}+r_{4}\ \ (0<r_{4}<r_{3})}$

${\displaystyle ...}$

${\displaystyle r_{h-1}=k_{h-1}r_{h}+0}$

が得られるとき、

${\displaystyle {\begin{pmatrix}r_{0}\\r_{1}\\\end{pmatrix}}={\begin{pmatrix}k_{0}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}r_{1}\\r_{2}\\\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}r_{1}\\r_{2}\\\end{pmatrix}}={\begin{pmatrix}k_{1}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}r_{2}\\r_{3}\\\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}r_{2}\\r_{3}\\\end{pmatrix}}={\begin{pmatrix}k_{2}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}r_{3}\\r_{4}\\\end{pmatrix}}}$

${\displaystyle ...}$

${\displaystyle {\begin{pmatrix}r_{h-1}\\r_{h}\\\end{pmatrix}}={\begin{pmatrix}k_{h-1}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}r_{h}\\0\\\end{pmatrix}}}$

すなわち

${\displaystyle {\begin{pmatrix}r_{0}\\r_{1}\\\end{pmatrix}}={\begin{pmatrix}k_{0}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}k_{1}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}k_{2}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}k_{3}&1\\1&0\\\end{pmatrix}}...{\begin{pmatrix}k_{h-1}&1\\1&0\\\end{pmatrix}}{\begin{pmatrix}r_{h}\\0\\\end{pmatrix}}}$

ここで

${\displaystyle K_{i}={\begin{pmatrix}k_{i}&1\\1&0\\\end{pmatrix}}}$ とおくと、${\displaystyle |K_{i}|=-1}$ であるから${\displaystyle K_{i}^{-1}}$は存在して

${\displaystyle {\begin{pmatrix}k_{h-1}&1\\1&0\\\end{pmatrix}}^{-1}{\begin{pmatrix}k_{h-2}&1\\1&0\\\end{pmatrix}}^{-1}...{\begin{pmatrix}k_{2}&1\\1&0\\\end{pmatrix}}^{-1}{\begin{pmatrix}k_{1}&1\\1&0\\\end{pmatrix}}^{-1}{\begin{pmatrix}k_{0}&1\\1&0\\\end{pmatrix}}^{-1}{\begin{pmatrix}r_{0}\\r_{1}\\\end{pmatrix}}={\begin{pmatrix}r_{h}\\0\\\end{pmatrix}}}$

これらの過程において、${\displaystyle m=r_{0},n=r_{1}}$、ユークリッドの互除法により、${\displaystyle r_{h}=\gcd(m,n)}$であるから、${\displaystyle K_{i}^{-1}={\begin{pmatrix}0&1\\1&-k_{i}\\\end{pmatrix}}}$を考慮すると、

${\displaystyle {\begin{pmatrix}0&1\\1&-k_{h-1}\\\end{pmatrix}}{\begin{pmatrix}0&1\\1&-k_{h-2}\\\end{pmatrix}}...{\begin{pmatrix}0&1\\1&-k_{2}\\\end{pmatrix}}{\begin{pmatrix}0&1\\1&-k_{1}\\\end{pmatrix}}{\begin{pmatrix}0&1\\1&-k_{0}\\\end{pmatrix}}{\begin{pmatrix}m\\n\\\end{pmatrix}}={\begin{pmatrix}\gcd(m,n)\\0\\\end{pmatrix}}}$

となる。

${\displaystyle {\begin{pmatrix}x&y\\u&v\\\end{pmatrix}}={\begin{pmatrix}0&1\\1&-k_{h-1}\\\end{pmatrix}}{\begin{pmatrix}0&1\\1&-k_{h-2}\\\end{pmatrix}}...{\begin{pmatrix}0&1\\1&-k_{2}\\\end{pmatrix}}{\begin{pmatrix}0&1\\1&-k_{1}\\\end{pmatrix}}{\begin{pmatrix}0&1\\1&-k_{0}\\\end{pmatrix}}}$

とおき、ユークリッドの互除法の各過程で得られた ${\displaystyle k_{0}}$, ${\displaystyle k_{1}}$, ${\displaystyle k_{2}}$等を用いて、右辺を計算すれば、左辺の${\displaystyle x}$, ${\displaystyle y}$ が求まり、これはベズーの等式

${\displaystyle mx+ny=\gcd(m,n)}$

を満たす^[6]。

計算量

割って余りを取るという操作を最悪でも小さいほうの十進法での桁数の約 5 倍繰り返せば、最大公約数に達する（ラメの定理）。

最大公約数を求めるのに素因数分解すればよいと思うかもしれないが、この定理は（m, n が大きいときには）素因数分解をするよりもユークリッドの互除法によるほうがはるかに速いということを述べている。

実際、計算複雑性理論においては最大公約数を求めることは「容易な問題」として知られており、素因数分解は「困難な問題」であろうと考えられている。 入力された2つの整数のうち小さいほうの整数 n の桁数を d とすれば、ユークリッドの互除法では O(d) 回の除算で最大公約数が求められる。桁数 d は O(log n) なので、ユークリッドの互除法では O(log n) 回の除算で最大公約数が求められる。

連分数

上の例で出てきた、1071 と 1029 の最大公約数を求める過程は、次のように表せる。

${\displaystyle {\begin{aligned}1071&=1029\times 1+42,\\1029&=42\times 24+21,\\42&=21\times 2.\end{aligned}}}$

すなわち、

${\displaystyle {\begin{aligned}{\frac {1071}{1029}}&=1+{\frac {42}{1029}},\\{\frac {1029}{42}}&=24+{\frac {21}{42}},\\{\frac {42}{21}}&=2.\end{aligned}}}$

したがって、

${\displaystyle {\frac {1071}{1029}}=1+{\frac {1}{24+{\frac {1}{2}}}}}$

このように、 n と m (n > m) の最大公約数を求める際のユークリッドの互除法の割り算の商は、有理数 n/m の連分数展開になっている。