ホモロジー代数学

ホモロジー代数学（ホモロジーだいすうがく、英: homological algebra）は、一般の代数的な設定のもとでホモロジーを研究する数学の分野である。それは比較的新しい分野であり、その起源は19世紀の終わりの、組み合わせ論的トポロジー（英語版）（代数トポロジーの前身）と抽象代数学（加群や syzygy（英語版） の理論）の、主にアンリ・ポアンカレとダフィット・ヒルベルトによる研究にまでさかのぼる。

ホモロジー代数学における基本的な結果である蛇の補題で用いられる図式。

ホモロジー代数学の発展は圏論の出現と密接に結びついている。概して、ホモロジー代数はホモロジー的関手とそれから必然的に生じる複雑な代数的構造の研究である。数学においてきわめて有用で遍在する概念の1つはチェイン複体 (chain complex) の概念であり、これはそのホモロジーとコホモロジーの両方を通じて研究できる。ホモロジー代数は、これらの複体に含まれる情報を得、それを環、加群、位相空間や、他の 'tangible' な数学的対象のホモロジー的不変量の形で描写する手段を提供してくれる。これをするための強力な手法はスペクトル系列によって与えられる。

まさにその起源から、ホモロジー代数学は代数トポロジーにおいて非常に多くの役割を果たしている。その影響の範囲は徐々に拡大しており現在では可換環論、代数幾何学、代数的整数論、表現論、数理物理学、作用素環論、複素解析、そして偏微分方程式論を含む。K-理論はホモロジー代数学の手法を利用する独立した分野であり、アラン・コンヌの非可換幾何もそうである。

ホモロジー代数学の歴史

ホモロジー代数学は1800年代にトポロジーの1つの分野としてその最も基本的な形が研究され始めたが、Ext関手やTor関手のような対象の研究が独立した主題になるのは1940年代になってからであった^[1]。

チェイン複体とホモロジー

→詳細は「鎖複体」を参照

チェイン複体 (chain complex) はホモロジー代数学の中心的な概念である。それはアーベル群と群準同型の列 ${\displaystyle (C_{\bullet },d_{\bullet })}$ であって、任意の2つの連続した写像の合成が 0 になるという性質をもったものである。

${\displaystyle C_{\bullet }:\cdots \longrightarrow C_{n+1}{\stackrel {d_{n+1}}{\longrightarrow }}C_{n}{\stackrel {d_{n}}{\longrightarrow }}C_{n-1}{\stackrel {d_{n-1}}{\longrightarrow }}\cdots ,\quad d_{n}\circ d_{n+1}=0.}$

C_n の元は n-チェイン（n-chain）と呼ばれ、準同型 d_n はバウンダリ写像 (boundary map) や微分 (differential) と呼ばれる。チェイン群 (chain group) C_n は余分な構造をもっているかもしれない。例えば、ベクトル空間や、固定された環 R 上の加群かもしれない。微分は余分な構造もそれが存在するならば保たなければならない。例えば、線型写像や R-加群の準同型でなければならない。表記の都合のため、アーベル群（より正確には、アーベル群の圏 Ab）に注意を制限しよう。名高いミッチェルの埋め込み定理によって、結果は任意のアーベル圏に一般化される。すべてのチェイン複体はさらに2つのアーベル群の列を定義する。サイクル (cycle) Z_n = Ker d_n とバウンダリ (boundary) B_n = Im d_n+1 である。ただし Ker d と Im d は d の核と像を表す。2つの連続するバウンダリ写像の合成は 0 なので、これらの群は互いの中に次のように埋め込まれている。

${\displaystyle B_{n}\subseteq Z_{n}\subseteq C_{n}.}$

アーベル群の部分群は自動的に正規である。したがって、n 次 ホモロジー群 (nth homology group) H_n(C) を n-サイクルの n-バウンダリによる商群

${\displaystyle H_{n}(C)=Z_{n}/B_{n}=\operatorname {Ker} \,d_{n}/\operatorname {Im} \,d_{n+1}.}$

として定義できる。チェイン複体は、すべてのそのホモロジー群が 0 であるときに、非輪状 (acyclic) または完全列、完全系列 (exact sequence) と呼ばれる。

チェイン複体は代数学や代数トポロジーにおいてよく現れる。例えば、X が位相空間であれば、その特異チェイン C_n(X) は標準 n-単体から X の中への連続写像の形式的な線型結合である。K が単体的複体であれば単体的チェイン（英語版） C_n(K) は X の n-単体の形式的な線型結合である。A = F/R がアーベル群 A の生成元と関係式による表現、ただし F は生成元で張られた自由アーベル群で R は relations の部分群、であれば、C₁(A) = R, C₀(A) = F, そしてすべての他の n に対して C_n(A) = 0 とすることによって、アーベル群の列が定義される。これらのケースではすべて、C_n を複体にする自然な微分 d_n が存在する。その複体のホモロジーは位相空間 X、単体的複体 K、あるいはアーベル群 A の構造を反映している。位相空間のケースでは、特異ホモロジーの概念に到達する。これはそのような空間例えば多様体の性質を研究する際に基本的な役割を果たす。 哲学的なレベルでは、ホモロジー代数学は、代数的あるいは幾何学的対象（位相空間、単体的複体、R-加群）に伴ったチェイン複体は、ホモロジーは最も容易に得られる部分でしかないが、それらについてたくさんの価値ある代数的情報を含む、ということを教えてくれる。専門的なレベルでは、ホモロジー代数学は複体を巧みに処理しこの情報を抽出するためのツールを提供する。ここに2つの一般的な例がある。

• 2つの対象 X と Y がそれらの間の写像 f で結ばれている。ホモロジー代数学は f によって誘導される、X と Y に伴うチェイン複体とそれらのホモロジーの間の関係を研究する。これは複数の対象とそれらをつなげる写像の場合に一般化される。圏論の言葉で言えば、ホモロジー代数学はチェイン複体とこれらの複体のホモロジーのさまざまな構造の関手的性質を研究する。
• 対象 X は複数の記述ができる（例えば、位相空間としておよび単体的複体として）、または、複体 ${\displaystyle C_{\bullet }(X)}$ は自然でない選択を含む X のある '表現' を使って構成される。X に伴ったチェイン複体の X の記述の変更の効果を知ることが重要である。一般的には、複体とそのホモロジー ${\displaystyle H_{\bullet }(C)}$ はその表現に関して関手的である。そしてホモロジーは（複体自身でないけれども）選択した表現とは実は独立であり、したがってそれは X の不変量である。

基本的な手法

完全列

→詳細は「完全列」を参照

群論の文脈では、群と群準同型の列

${\displaystyle G_{0}\;{\xrightarrow {f_{1}}}\;G_{1}\;{\xrightarrow {f_{2}}}\;G_{2}\;{\xrightarrow {f_{3}}}\;\cdots \;{\xrightarrow {f_{n}}}\;G_{n}}$

は、次のようなときに完全 (exact) という。各準同型の像（あるいは値域）が次の準同型の核に等しい。

${\displaystyle \mathrm {im} (f_{k})=\mathrm {ker} (f_{k+1}).\!}$

群と準同型の列の長さは有限でも無限でもよいことに注意する。

同様の定義はある種の他の代数的構造に対してもすることができる。例えば、ベクトル空間と線型写像の完全列や、加群と加群準同型の完全列がある。より一般的に、完全列の概念は、核と余核ともった任意の圏において意味をもつ。

短完全列

完全列の最もよく現れるタイプは短完全列 (short exact sequence) である。これは

${\displaystyle A\;{\overset {f}{\hookrightarrow }}\;B\;{\overset {g}{\twoheadrightarrow }}\;C}$

の形の完全列である。ただし ƒ はモノ射で g はエピ射である。この場合、A は B の部分対象であり、対応する商は C に同型である。

${\displaystyle C\cong B/f(A)}$

（ただし f(A) = im(f)）。

アーベル群の短完全列は5つの項をもった完全列として書くこともできる。

${\displaystyle 0\;{\xrightarrow {}}\;A\;{\xrightarrow {f}}\;B\;{\xrightarrow {g}}\;C\;{\xrightarrow {}}\;0}$

ただし 0 は自明群や0次元ベクトル空間といった零対象を表す。0 の配置によって ƒ は単射であり g はエピ射になる（下記参照）。

長完全列

長完全列は自然数で添え字づけられた完全列である。

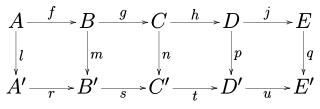
五項補題

→詳細は「5項補題」を参照

任意のアーベル圏（アーベル群の圏や与えられた体上のベクトル空間の圏など）や群の圏において以下の可換図式を考える。

5項補題は次のものである。2つの列が完全で、m と p が同型射で、l がエピ射で、q がモノ射であれば、n も同型である。

蛇の補題

→詳細は「蛇の補題」を参照

任意のアーベル圏（アーベル群の圏や与えられた体上のベクトル空間の圏など）において、可換図式

を考える。ただし2つの列は完全で、0 は零対象である。すると a, b, c の核や余核に関連した完全列

${\displaystyle \ker a\;{\color {Gray}\longrightarrow }\ker b\;{\color {Gray}\longrightarrow }\ker c\;{\overset {d}{\longrightarrow }}\operatorname {coker} a\;{\color {Gray}\longrightarrow }\operatorname {coker} b\;{\color {Gray}\longrightarrow }\operatorname {coker} c}$

が存在する。さらに、射 f がモノ射であれば、射 ker a → ker b もモノ射であり、g' がエピ射であれば、coker b → coker c もエピ射である。

アーベル圏

→詳細は「アーベル圏」を参照

数学において、アーベル圏 (abelian category) は、射や対象を足すことができ、核や余核が存在し望ましい性質をもった圏である。動機付けるプロトタイプのアーベル圏の例はアーベル群の圏 Ab である。理論の起源は アレクサンドル・グロタンディーク (Alexander Grothendieck) によるいくつかのコホモロジー論を統合しようとする試験的な試みである。アーベル圏はとても安定 (stable) である。例えば、正則（英語版）であり、蛇の補題を満たす。アーベル圏のクラスはいくつかの圏論的構成で閉じている。例えば、アーベル圏のチェイン複体の圏や、小さい圏からアーベル圏への関手の圏は、再びアーベル圏である。これらの安定性によってアーベル圏はホモロジー代数学やその先で必要不可欠なものである。理論は代数幾何学、コホモロジー、そして純粋に圏論において、主要な応用をもつ。アーベル圏は ニールス・アーベル (Niels Henrik Abel) にちなんで名づけられている。

より具体的には、圏がアーベル圏であるとは以下を満たすことである。

• 零対象をもつ。
• すべて二項の積と二項の余積をもつ。
• すべて核と余核をもつ。
• すべてのモノ射とエピ射は正規射（英語版）である。

Ext 関手

→詳細は「Ext関手」を参照

R を環とし、Mod_R を R 上の加群の圏とする。B in Mod_R とし、固定された A in Mod_R に対し T(B) = Hom_R(A,B) とおく。これは左完全関手でありしたがって右導来関手 RⁿT をもつ。Ext 関手は

${\displaystyle \operatorname {Ext} _{R}^{n}(A,B)=(R^{n}T)(B)}$

で定義される。これは任意の移入分解

${\displaystyle 0\rightarrow B\rightarrow I^{0}\rightarrow I^{1}\rightarrow \dots }$

をとり

${\displaystyle 0\rightarrow \operatorname {Hom} _{R}(A,I^{0})\rightarrow \operatorname {Hom} _{R}(A,I^{1})\rightarrow \dots }$

を計算することによって計算できる。すると (RⁿT)(B) はこの複体のホモロジーである。Hom_R(A,B) は複体から除かれていることに注意せよ。

関手 G(A)=Hom_R(A,B) を使って別の定義が与えられる。固定された加群 B に対し、これは反変左完全関手であり、したがって右導来関手 RⁿG ももっており、

${\displaystyle \operatorname {Ext} _{R}^{n}(A,B)=(R^{n}G)(A)}$

と定義できる。これは任意の射影分解

${\displaystyle \dots \rightarrow P^{1}\rightarrow P^{0}\rightarrow A\rightarrow 0,}$

を選び、

${\displaystyle 0\rightarrow \operatorname {Hom} _{R}(P^{0},B)\rightarrow \operatorname {Hom} _{R}(P^{1},B)\rightarrow \dots }$

を計算して双対的に続けることによって計算できる。すると (RⁿG)(A) はこの複体のホモロジーである。Hom_R(A,B) が除かれていることに再び注意する。

これらの2つの構成は同型な結果をもたらすことがわかり、したがって Ext 関手を計算するのにどちらを使ってもよい。

Tor 関手

→詳細は「Tor関手」を参照

R を環とし、R-Mod によって左 R-加群の圏を、Mod-R によって右 R-加群の圏を表記する。（R が可換環であれば、2つの圏は一致する。固定された加群 B in R-Mod を選ぶ。A in Mod-R に対し、T(A) = A⊗_RB とおく。すると T は Mod-R からto the アーベル群の圏 Ab への右完全関手である（R が可換なときには、Mod-R から Mod-R への右完全関手である）。そしてその左導来関手 L_nT が定義される。

${\displaystyle \mathrm {Tor} _{n}^{R}(A,B)=(L_{n}T)(A)}$

とおく。すなわち、射影分解

${\displaystyle \cdots \rightarrow P_{2}\rightarrow P_{1}\rightarrow P_{0}\rightarrow A\rightarrow 0}$

をとり、A の項を取り除き、射影分解を B でテンソルして複体

${\displaystyle \cdots \rightarrow P_{2}\otimes _{R}B\rightarrow P_{1}\otimes _{R}B\rightarrow P_{0}\otimes _{R}B\rightarrow 0}$

を得る。（A⊗_RB は現れず、最後の矢はただの零写像であることに注意する。）そしてこの複体のホモロジーをとる。

スペクトル系列

→詳細は「スペクトル系列」を参照

環上の加群の圏のようなアーベル圏を固定する。スペクトル（系）列 (spectral sequence) は非負整数 r₀ の選択と3つの列の集まりである。

1. すべての整数 r ≥ r₀ に対して、対象 E_r。（紙のシートのように）シート (sheet) と呼ばれる。ページ (page) やターム (term) と呼ばれることもある。
2. d_r o d_r = 0 を満たす自己準同型 d_r : E_r → E_r。境界写像 (boundary map) や微分 (differential) と呼ばれる。
3. d_r に関する E_r のホモロジー H(E_r) による E_r+1 の同型

The E₂ sheet of a cohomological spectral sequence

二重に次数付けられたスペクトル列は把握するには途方もない量のデータをもっている。しかし、スペクトル列の構造を明確にする、一般的な視覚化のテクニックがある。3つの添え字 r, p, q がある。各 r に対し、グラフ用紙のシートを1枚もっていると想像しよう。このシートの上に、p を水平な向きに、q を垂直な向きにとる。各格子点に、対象 ${\displaystyle E_{r}^{p,q}}$ があるのである。

n = p + q がスペクトル列の別の自然な添え字であることは非常によくある。n は北西から南東に対角線上を動き、各シートを渡る。ホモロジーの場合には、微分は bidegree (−r, r − 1) をもっているので、n が1つ減る。コホモロジーの場合には、n は1増える。r が 0 であるときには、微分は1つ下か上に対象を動かす。これはチェイン複体上の微分に似ている。r が 1 であるときには、微分は1つ左か右に対象を動かす。r が 2 であるときには、微分はちょうどチェスのナイトの動きのように対象を動かす。より大きい r に対しては、微分はナイトの動きを一般化したような感じで作用する。

導来関手

→詳細は「導来関手」を参照

2つのアーベル圏 A と B の間に共変左完全関手 F : A → B が与えられているとしよう。0 → A → B → C → 0 が A における短完全列であれば、F を施すことで完全列 0 → F(A) → F(B) → F(C) を得、次のことを疑問に思うだろう。この列を右に続けて長完全列にするにはどうすればいいだろうか。厳密に言えば、これは不良設定問題である。なぜならば与えられた完全列を右に続けるたくさんの異なる方法が常に存在するからである。しかし、（A が十分 "nice" であれば）それを行う1つのカノニカルな（英語版）方法が存在し、それは F の右導来関手によって与えられる、ということがわかる。すべての i≥1 に対して、関手 RⁱF: A → B が存在し、上記の列は以下のように続く。0 → F(A) → F(B) → F(C) → R¹F(A) → R¹F(B) → R¹F(C) → R²F(A) → R²F(B) → ... . これから F が完全関手であることと R¹F = 0 であることが同値であることがわかる。なのである意味 F の右導来関手は F が完全であることから「どの程度離れているか」を測る。

関手性

位相空間の連続写像はすべての n に対してそれらの n 次ホモロジー群の間の準同型を引き起こす。この代数トポロジーの基本的な結果はチェイン複体のある種の性質による自然な説明を見つける。いくつかの位相空間を同時に研究することは非常によくあることだから、ホモロジー代数において多数のチェイン複体を同時に考察するということになる。

2つのチェイン複体の間の射 (morphism) ${\displaystyle F:C_{\bullet }\to D_{\bullet }}$ はアーベル群の準同型 F_n:C_n → D_n の族であって微分と交換するようなものである。これの意味するところは、すべての n に対して、F_{n -1} •  d_n^C = d_n^D • F_n ということである。チェイン複体の射はそれらのホモロジー群の射 ${\displaystyle H_{\bullet }(F)}$ を誘導する。これはすべての n に対して準同型 H_n(F): H_n(C) → H_n(D) からなる。射 F は、それがすべての n に対して n 次ホモロジーの同型を誘導するときに、擬同型 (quasi-isomorphism) と呼ばれる。

代数や幾何で生じる、特異ホモロジーを含む、チェイン複体の多くの構成は、次の関手的性質をもっている。2つの対象 X と Y が写像 f で結ばれていれば、伴ったチェイン複体は ${\displaystyle C_{\bullet }(X)}$ から ${\displaystyle C_{\bullet }(Y)}$ への射 F = C(f) によって結ばれており、さらに、写像 f: X → Y と g: Y → Z の合成 g • f は、合成 C(g) • C(f) と一致する、${\displaystyle C_{\bullet }(X)}$ から ${\displaystyle C_{\bullet }(Z)}$ への射 C(g • f) を誘導する。ホモロジー群 ${\displaystyle H_{\bullet }(C)}$ もまた関手的であるということが従い、それゆえ代数的あるいは幾何学的対象の間の射はそれらのホモロジーの間の両立する (compatible) 写像を引き起こす。

次の定義は代数やトポロジーでよくある状況から生じる。3つのチェイン複体 ${\displaystyle L_{\bullet },M_{\bullet },N_{\bullet }}$ とそれらの間の2つの射${\displaystyle f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet }}$ からなる三つ組みは次のようなとき exact triple あるいは複体の短完全列 (short exact sequence of complexes) と呼ばれ、

${\displaystyle 0\longrightarrow L_{\bullet }{\stackrel {f}{\longrightarrow }}M_{\bullet }{\stackrel {g}{\longrightarrow }}N_{\bullet }\longrightarrow 0,}$

と書かれる：任意の n に対して、列

${\displaystyle 0\longrightarrow L_{n}{\stackrel {f_{n}}{\longrightarrow }}M_{n}{\stackrel {g_{n}}{\longrightarrow }}N_{n}\longrightarrow 0}$

はアーベル群の短完全列である。定義によって、このことは f_n は単射で、g_n は全射で、 Im f_n =  Ker g_n であることを意味する。ジグザグ補題と呼ばれることもある、ホモロジー代数学の最も基本的な定理の1つによると、この場合、ホモロジーの長完全列

${\displaystyle \ldots \longrightarrow H_{n}(L){\stackrel {H_{n}(f)}{\longrightarrow }}H_{n}(M){\stackrel {H_{n}(g)}{\longrightarrow }}H_{n}(N){\stackrel {\delta _{n}}{\longrightarrow }}H_{n-1}(L){\stackrel {H_{n-1}(f)}{\longrightarrow }}H_{n-1}(M)\longrightarrow \ldots }$

が存在する。L, M, N のホモロジー群は循環的に互いに従い、δ_n は f と g によって決定されるある準同型であり、連結準同型 (connecting homomorphism) と呼ばれる。この定理を位相幾何学的に表現すれば、マイヤー・ヴィートリス完全系列や相対ホモロジー（英語版）の長完全列が現れる。

基礎的な見地

コホモロジー論は、位相空間、層、群、環、リー環、そしてC*-環といった、多くの異なる対象に対して定義されてきた。現代的な代数幾何学の研究は層コホモロジーなしではほとんど考えられないであろう。

ホモロジー代数学で中心的なのは完全列の概念である。これらは実際の計算を行うのに使うことができる。ホモロジー代数学の古典的な手法は導来関手のそれである。最も基本的な例は関手 Ext と Tor である。

様々な応用が念頭にあり、主題全体を一定の基礎の上に置こうとすることは自然だった。主題が落ち着くまでにいくつかの試みがあった。大体の経過は以下のように述べられる。

• Cartan–Eilenberg： 彼らの 1956 年の本 "Homological Algebra" において、これらの著者は射影および移入加群分解を用いた。
• 'Tohoku'（東北）： Alexander Grothendieck による名高い論文におけるアプローチ。1957年にTohoku Mathematical Journal（東北数学雑誌）の Second Series に現れ、（アーベル群の層を含むために）アーベル圏の概念を使っている。
• Grothendieck と ジャン・ルイ・ヴェルディエ（英語版） (Jean-Louis Verdier) の導来圏。導来圏は Verdier の1967年の学位論文までさかのぼる。これは多くの現代理論で使われる三角圏（英語版） の例である。

これらは計算可能性から一般性へと進展する。

一段とすぐれた (par excellence) 計算のスレッジハンマーはスペクトル系列である。これは例えば2つの関手の合成の導来関手を計算するのに必要である Cartan–Eilenberg や Tohoku のアプローチにおいて必須である。スペクトル系列は導来圏のアプローチでは重要性は落ちるがそれでも具体的な計算が必要なときにはいつでも役割を果たす。

はじめのコホモロジーを torsor（英語版） として拡張する '非可換' 理論の試みがなされている（ガロワ・コホモロジーにおいて重要である）。

関連項目

• アブストラクト・ナンセンス、ホモロジー代数学と圏論に対する用語
• Derivator
• ホモトピー代数学
• 環論
• ホモロジー代数学のトピック一覧（英語版）

脚注

1. History of Homological Algebra, by Chuck Weibel, pp.797-836 in the book The History of Topology, ed. I.M. James, Elsevier, 1999

参考文献

• Henri Cartan, Samuel Eilenberg, Homological algebra. With an appendix by David A. Buchsbaum. Reprint of the 1956 original. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp. ISBN 0-691-04991-2
• Alexander Grothendieck, Sur quelques points d'algèbre homologique. Tôhoku Math. J. (2) 9, 1957, 119–221
• Saunders Mac Lane, Homology. Reprint of the 1975 edition. Classics in Mathematics. Springer-Verlag, Berlin, 1995. x+422 pp. ISBN 3-540-58662-8
• Peter Hilton; Stammbach, U. A course in homological algebra. Second edition. Graduate Texts in Mathematics, 4. Springer-Verlag, New York, 1997. xii+364 pp. ISBN 0-387-94823-6
• Gelfand, Sergei I.; Yuri Manin, Methods of homological algebra. Translated from Russian 1988 edition. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. xx+372 pp. ISBN 3-540-43583-2
• Gelfand, Sergei I.; Yuri Manin, Homological algebra. Translated from the 1989 Russian original by the authors. Reprint of the original English edition from the series Encyclopaedia of Mathematical Sciences (Algebra, V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Berlin, 1999. iv+222 pp. ISBN 3-540-65378-3
• Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324