頻度分析 (暗号)

暗号技術において、頻度分析（Frequency analysis、ひんどぶんせき）は、平文と暗号文に使用される文字や文字列の出現頻度を手掛りとして利用する暗号解読法のことである。平文の言語の統計的特徴を前提とし、暗号文のみを使用して解読を行うため、暗号文単独攻撃に分類される。

概要

平文の1文字を別の文字（や数字、記号等）に1対1で変換して暗号文を作成する単一換字式暗号には、平文と暗号文で対応する文字の出現頻度が一致するという特徴がある。通常、平文の文字の出現頻度には顕著な偏りがあり、この偏りは文章によらずほぼ一定であるため、平文の文字の出現頻度と暗号文の文字の出現頻度を照らし合わせることで、平文と暗号文の文字の対応関係を特定でき、暗号文を解読できる。

使用される文字の種類とその出現頻度は英語やドイツ語、日本語など言語によって異なるので、頻度分析を行うことにより平文の言語を推定することが可能である。さらに、組織や個人によっても出現頻度に違いがある場合があり、頻度分析の精度を向上させるのに利用できる。 また、暗号文は文字で構成されるとは限らず、数字や記号が使用されることもある。例として、平文の1文字に2桁の数を対応させるポリュビオスの暗号表がある。この場合には暗号文の数字2桁が平文の1文字に対応することを推定した上で、頻度分析を試みることになる。

頻度分析が有効なのは、主に古典暗号の換字式暗号であり、9世紀にアラビア人のキンディーが執筆した暗号文書の解読に関する手記にこの解読法の記述がある。15世紀頃にはルネサンスにより欧州にも広がり、ヴィジュネル暗号のような多表式換字の考案の動機となり、20世紀に到るまで、新たな暗号方式の提案と頻度分析をベースとする解読法の改良が繰り返された。20世紀初頭に開発された機械式暗号によって、単純な頻度分析は適用困難になり、暗号解読はアルゴリズムの数学的分析を伴う研究へと変質していった。現代暗号では、暗号文単独攻撃よりも厳しい既知平文や選択暗号文の条件でも安全であることを目標として設計され、ここでは、平文の言語的な特徴を手掛りとする頻度分析は克服されている。

頻度分析の考え方は暗号解読だけではなくて、古代文字の解読にも利用される。

適用

英文字の出現頻度

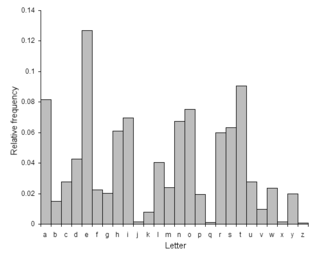
英語の一般的な文章の場合、アルファベット（単文字）を数え上げてヒストグラムを作成すると（右図参照）、概ね e, t, a, o, i, n, ..., j, x, q, z の順で出現することが分る。 同様に2文字（連接文字）の場合、t-h, h-e, i-n, e-r, ... 、3文字の場合には、t-h-e, a-n-d, i-n-g, i-o-n, ... などの順で出現頻度が高いことが知られている。連接文字の場合、'q' の次には 'u' が出現するなどの条件付きの出現頻度に特徴がある場合もある。この特徴を連接特徴という。さらにスペース（単語の区切り）が判明する場合には、単語の出現頻度を利用できる。

暗号解読には出現頻度だけではなくて、出現間隔（反復特徴）も貴重な手掛りとなる。反復特徴には、自己反復、相対反復、一致反復、文内反復がある。詳細は、一致反復率を参照。

平文の文字の出現頻度は、文章によって多少のバラツキはあり、暗号文が少ない場合には出現数の誤差も多くなる。暗号を使用するような組織では、固有名詞や文体の影響で、一般的な出現頻度と異なる場合もあるし、意図的に操作することも可能である。その例として、e を全く使用しないで書かれた小説も存在する（ジョルジュ・ペレック著『消失（La Disparition）』仏語, 1969年、ギルバート・アデア訳『消失（A Void）』英訳, 1994年）。

解読作業は出現頻度などの統計量を手掛りに、1文字ずつ平文の文字を推定して、矛盾がでたら一つ戻って次の文字を試すことを繰り返す。文字の推定は、出現頻度に特徴がある文字から割り当て、これには出現頻度が高い文字と低い文字の両方が利用できる。文法上や前後の単語から意味を考慮して文字を絞り込めることもある。このように頻度分析を実際に行う解読要員には単調な文字を数え上げ作業をこなす能力とクロスワードパズルを解くようなセンスが必要とされる。第二次大戦時には、イギリスやアメリカは、新聞にクロスワードパズルを掲載して、暗号解読要員の募集をしている。文字の数え上げ作業の機械化は、第2次大戦になってIBMのマシンによって始められた。

文学の世界では、「黄金虫」（ポー、1843年）や「踊る人形」（ドイル、1903年）などの暗号小説にて、このような頻度分析のテクニックが謎解きの一場面として描かれている。

歴史

頻度分析に関する最古の記録は、9世紀のキンディーによる、暗号文書の解読に関する手記である（これは暗号解読法に関する最古の記録でもある）。(stub)

この解読法は、ルネサンスにより15世紀頃には欧州にも広がった。当時の欧州では、シフト暗号を複雑にして変換ルールが見破られないように工夫した鍵付き換字等が使用されていた。頻度分析は、換字表がどのように複雑であっても分析可能であり、これらの工夫をすべてを無効にできる。16世紀には外交官にあてた暗号文の多くが他国に解読されていたという。 このように頻度分析によって、単一換字暗号の安全性が失われると、頻度分析への対策として次のような方式が考案された。参照：換字式暗号#分類

同音換字 (homophonic substitution cipher)

平文の1文字（eなど）に、暗号文の複数の文字(x, q, zなど)を対応させ、その一つをランダムに選択して変換することで、暗号文の出現頻度の偏りを少なくする。1401年に同音換字が使用された記録がある。

多表式換字 (polyalphabetic substitution cipher)

ヴィジュネル暗号（1586年）など。複数の変換表を鍵に従って切替えて使用する。平文の1文字に対応する暗号文の文字が、変換表の切替えに従い、変化するため、暗号文の文字の出現頻度が攪拌されて偏りが少なくなる。

綴字換字 (polygraphic substitution cipher)

プレイフェア暗号（1854年）やヒル暗号など。複数文字を複数文字に対応させる。2文字をdigram、3文字のものをtrigramという。暗号文の1文字単位の出現頻度を錯乱できる。

これらの新型の換字式暗号、特に多表式換字は手作業で行うには暗号化/復号処理が複雑なため、当初は敬遠されていたが、18世紀頃には採用されるようになり、ヴィジュネル暗号は19世紀中頃までの300年近く解読不能と考えられていた。頻度分析で解読できない換字式暗号が広まると、それを打ち負かすように、複数文字の出現頻度の考慮や鍵周期の特定など、頻度分析を改良する考案もなされた。

カシスキーテスト（19世紀）

1863年にプロシアのフリードリヒ・カシスキが出版した書籍にて公開（後にチャールズ・バベッジが1854年頃に発見していたことが判明）。ヴィジュネル暗号は、単純な頻度分析では解読できないが、同一文字列の出現周期から鍵周期を特定することによって、頻度分析を適用できる（単純なシフト暗号に帰着できる）ことが指摘された。多表式換字では、同一の文字列（"the" のような文字の並び）に対応する暗号文は、鍵の長さ分だけのバリエーションがあり、かつ鍵周期に従って選択されるため、暗号文中に同一の並びが出現する間隔は（偶然に一致する場合を除くと）鍵周期の公倍数になる。鍵周期の公倍数となる値を複数個集めて最大公約数を求めると鍵周期を得ることができる。周期判定法ともいう。

一致反復率（20世紀）

1922年に米国のフリードマンが考案。鍵周期を特定して、多表式換字に頻度分析を適用できるようにする点はカシスキーテストと同じだが、鍵周期の長さを統計量的に扱う点が異なる。暗号文からランダムに2文字を選んだときに、その２文字が一致する確率から鍵周期の長さの目安とする。確率的な指標なので鍵周期を特定できるわけではない。

改良版も含めた頻度分析に対して十分安全と言える換字式暗号が実現されたのは、ロータ式暗号機（機械式暗号の一種）が開発された20世紀初頭になってのことである。エニグマ暗号機では、鍵周期が 26^3=17,576（ローターが3枚の場合）と十分に長くなるように設計された。このような暗号機の多くも暗号機の仕様上の特徴や暗号文の統計的性質を分析することで解読されていった。

参考文献

• D.E.R. デニング『暗号とデータセキュリティ』培風館、1988年（2.2.1 単文字頻度分析 pp.66-70 等）
• 松井甲子雄『コンピュータによる 暗号解読法入門』、森北出版、1990年（1.6 反復調査 pp.29- 等）

関連項目

• 暗号理論 / 暗号解読 / 暗号化 / 暗号史
• en:Letter frequency