Triangolo

Il triangolo è un poligono con tre lati.

Disambiguazione – Se stai cercando altri significati, vedi Triangolo (disambigua).

Caratteristiche del triangolo

La somma degli angoli interni di un triangolo è uguale a 180°.

Il triangolo è caratterizzato dalle seguenti proprietà:

1. è una "figura indeformabile", dato che, assegnate le lunghezze dei lati, sono univocamente determinati anche gli angoli; ciò non è vero in generale per poligoni con un numero maggiore di lati;
2. è l'unico poligono che non può essere concavo;
3. è l'unico poligono per cui non è richiesto che sia regolare perché sia sempre possibile circoscrivere e inscrivere una circonferenza, perché per tre punti passa sempre una e una sola circonferenza;
4. la somma degli angoli interni è uguale a un angolo piatto, ossia 180°; va comunque precisato che tale uguaglianza vale soltanto nella geometria euclidea e non in altri tipi di geometria come la geometria sferica e quella iperbolica, dove invece tale somma è, rispettivamente, maggiore e minore di 180°;
5. la somma di due lati deve essere sempre maggiore del terzo lato o la differenza di due lati deve essere sempre minore del terzo lato.

Due triangoli sono congruenti se soddisfano almeno uno dei criteri di congruenza.

Due triangoli si dicono simili se soddisfano almeno uno dei criteri di similitudine.

Classificazione dei triangoli

I triangoli possono essere classificati in base alla lunghezza relativa dei lati:

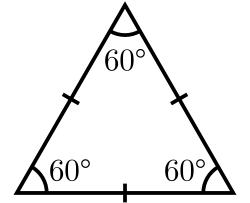
• In un triangolo equilatero tutti i lati hanno lunghezza uguale. Un triangolo equilatero si può definire equivalentemente come triangolo equiangolo, ovvero triangolo avente i suoi angoli interni di uguale ampiezza, pari a 60°.
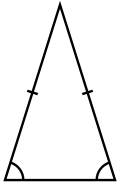
• In un triangolo isoscele due lati hanno lunghezza uguale. Un triangolo isoscele si può definire equivalentemente come triangolo avente due angoli interni di uguale ampiezza.
• In un triangolo scaleno tutti i lati hanno lunghezze differenti. Un triangolo scaleno si può definire equivalentemente come triangolo avente i tre angoli interni di diverse ampiezze ^[1].

Equilatero	Isoscele	Scaleno

I triangoli possono essere classificati anche in base alle dimensioni del loro angolo interno più ampio; sono descritti di seguito usando i gradi d'arco.

• Un triangolo rettangolo (o triangolo retto) ha un angolo interno di 90°, cioè un angolo retto. Il lato opposto all'angolo retto è detto ipotenusa; è il lato più lungo del triangolo rettangolo. Gli altri due lati del triangolo sono detti cateti. Per questo triangolo vale il teorema di Pitagora.
• Un triangolo ottusangolo (o triangolo ottuso) ha un angolo interno maggiore di 90°, cioè un angolo ottuso.
• Un triangolo acutangolo (o triangolo acuto) ha tutti gli angoli interni minori di 90°, cioè ha tre angoli acuti.
• Un triangolo equiangolo, cioè se ha tutti gli angoli interni uguali, cioè di 60°, cioè se e solo se è un triangolo equilatero.

Per i triangoli che non sono rettangoli vale una generalizzazione del teorema di Pitagora nota in trigonometria come teorema di Carnot.

Rettangolo	Ottusangolo	Acutangolo

Triangoli degeneri e triangoli ideali

Si dice triangolo degenere un triangolo che presenta un angolo di 180°. Gli altri due angoli hanno necessariamente ampiezza zero, e un lato misura quanto la somma degli altri due: tale triangolo, come insieme di punti (graficamente), costituisce un segmento.

Si usa il termine triangolo degenere anche per una figura ottenuta come limite di un triangolo nel quale alcuni dei suoi vertici vanno all'infinito; tale figura si chiama anche triangolo ideale. Questa costruzione è molto usata in geometria iperbolica.

Un triangolo ideale con un vertice all'infinito risulta essere una striscia delimitata da un segmento e da due semirette che si estendono illimitatamente nella stessa direzione, ciascuna delle quali ha come estremità una di quelle del segmento; in particolare le rette possono essere ortogonali al segmento.

Punti notevoli

Ad ogni triangolo sono associati vari punti, ciascuno dei quali svolge un ruolo che, per qualche aspetto, lo qualifica come centrale per il triangolo stesso. Definiamo concisamente questi punti riferendoci ad un triangolo ${\displaystyle T}$ i cui vertici denotiamo con ${\displaystyle A}$, ${\displaystyle B}$ e ${\displaystyle C}$ e i cui lati opposti denotiamo rispettivamente con ${\displaystyle a}$, ${\displaystyle b}$ e ${\displaystyle c}$.

• ortocentro di ${\displaystyle T}$ è l'intersezione delle sue altezze;
• baricentro o centroide di ${\displaystyle T}$ è l'intersezione delle sue mediane;
• incentro di ${\displaystyle T}$ è l'intersezione delle sue tre bisettrici, ovvero il centro dell'incerchio di ${\displaystyle T}$;
• circocentro di ${\displaystyle T}$ è l'intersezione dei suoi tre assi, ovvero il centro della sua circonferenza circoscritta (vedi circumcerchio);
• excentro di ${\displaystyle T}$ opposto a un suo vertice ${\displaystyle A}$ è l'intersezione della sua bisettrice in ${\displaystyle A}$ e delle due bisettrici esterne relative ai due vertici rimanenti ${\displaystyle B}$ e ${\displaystyle C}$;
• punto di Bevan di ${\displaystyle T}$ è il circocentro del triangolo excentrale di ${\displaystyle T}$;
• punto di Apollonio di ${\displaystyle T}$ è l'intersezione dei tre segmenti che rispettivamente uniscono un vertice ${\displaystyle A}$ di ${\displaystyle T}$ con il punto nel quale l'excerchio di ${\displaystyle T}$ opposto ad ${\displaystyle A}$ è tangente al cerchio tangente ai tre excerchi di ${\displaystyle T}$;
• punto di Gergonne di ${\displaystyle T}$ è l'intersezione dei tre segmenti che rispettivamente uniscono un vertice ${\displaystyle A}$ di ${\displaystyle T}$ con il punto nel quale il lato di ${\displaystyle T}$ opposto ad ${\displaystyle A}$ è tangente dell'incerchio di ${\displaystyle T}$;
• punto di Nagel di ${\displaystyle T}$ è l'intersezione dei tre segmenti ciascuno dei quali unisce un vertice di ${\displaystyle T}$ con il punto nel quale il suo lato opposto è tangente del corrispondente excerchio;
• punto di Fermat di ${\displaystyle T}$ è l'intersezione dei tre segmenti ciascuno dei quali unisce un vertice ${\displaystyle A}$ di ${\displaystyle T}$ con il vertice non appartenente a ${\displaystyle T}$ del triangolo equilatero uno dei cui lati è il lato ${\displaystyle a}$ opposto ad ${\displaystyle A}$ ed esterno a ${\displaystyle T}$;
• punto di Napoleone di ${\displaystyle T}$ è l'intersezione dei tre segmenti che collegano ognuno un suo vertice ${\displaystyle A}$ con il centro del triangolo equilatero costruito, esternamente a ${\displaystyle T}$, sul lato ${\displaystyle a}$ opposto ad ${\displaystyle A}$;
• centro dei nove punti di ${\displaystyle T}$ è il centro del cosiddetto cerchio dei nove punti (o cerchio di Feuerbach) di ${\displaystyle T}$; questi nove punti comprendono i tre punti medi dei lati di ${\displaystyle T}$, i tre piedi delle altezze di ${\displaystyle T}$, i punti medi dei tre segmenti ciascuno dei quali unisce un vertice di ${\displaystyle T}$ con l'ortocentro di ${\displaystyle T}$.
• punto pedale di ${\displaystyle T}$ è l'intersezione di ciascuna delle tre rette perpendicolari ai lati di ${\displaystyle T}$.
• punto ceviano di ${\displaystyle T}$ è l'intersezione di tre rette ceviane.

Formulario

Formule trigonometriche

Si applica la trigonometria per trovare l'altezza ${\displaystyle h}$

L'area di un triangolo può essere trovata per via trigonometrica. Usando le lettere della figura a destra, l'altezza ${\displaystyle h=a\sin \gamma }$. Sostituendo questo nella formula trovata precedentemente (per via geometrica), ${\displaystyle S={\frac {1}{2}}ab\sin \gamma }$. L'area di un triangolo è quindi anche uguale al semiprodotto di due lati per il seno dell'angolo compreso.

Di conseguenza, per la nota identità ${\displaystyle \sin x=\sin(\pi -x)}$, l'area di un triangolo qualsiasi con i due lati ${\displaystyle a}$ e ${\displaystyle b}$ e l'angolo compreso ${\displaystyle \gamma }$, è uguale all'area del triangolo con gli stessi lati ${\displaystyle a}$ e ${\displaystyle b}$ ma con angolo compreso supplementare ${\displaystyle (\pi -\gamma )}$

L'area di un parallelogramma con due lati adiacenti ${\displaystyle a}$ e ${\displaystyle b}$ e angolo compreso ${\displaystyle \gamma }$ è il doppio di quella del triangolo che ha gli stessi dati, cioè ${\displaystyle ab\sin \gamma }$.

Per risolvere il triangolo, cioè determinare la misura di tutti i lati e angoli, dati due lati e l'angolo compreso fra di essi, o un lato e i due angoli adiacenti, si usano il teorema dei seni e il teorema del coseno, quest'ultimo meglio noto col nome di Carnot.

L'area ${\displaystyle {\mathcal {A}}}$ del triangolo può essere misurata con la formula matematica:

${\displaystyle {\mathcal {A}}={\frac {bh}{2}},}$

dove ${\displaystyle b}$ è la base e ${\displaystyle h}$ l'altezza ad essa relativa, perché il triangolo va visto come la metà di un parallelogramma di base ${\displaystyle b}$ e altezza ${\displaystyle h}$.

Alternativamente l'area del triangolo può essere calcolata con

${\displaystyle {\mathcal {A}}={\sqrt {p(p-a)(p-b)(p-c)}},}$

dove ${\displaystyle a}$, ${\displaystyle b}$ e ${\displaystyle c}$ sono i lati e ${\displaystyle p}$ il semiperimetro (formula di Erone).

Formule analitiche

Consideriamo un triangolo ${\displaystyle ABC}$ nel piano cartesiano individuato attraverso le coppie di coordinate dei vertici ${\displaystyle (x_{A},y_{A}),(x_{B},y_{B}),(x_{C},y_{C})}$.

La sua area ${\displaystyle {\mathcal {A}}}$ è data dall'espressione

${\displaystyle {\mathcal {A}}={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{pmatrix}}\right|={\frac {1}{2}}{\big |}x_{A}(y_{B}-y_{C})-x_{B}(y_{A}-y_{C})+x_{C}(y_{A}-y_{B}){\big |},}$

oppure con un'espressione che non utilizza il concetto di matrice

${\displaystyle {\mathcal {A}}={\frac {{\big |}(y_{B}-y_{A})(x_{C}-x_{B})+(y_{B}-y_{C})(x_{B}-x_{A}){\big |}}{2}},}$

e il suo perimetro ${\displaystyle {\mathcal {P}}}$ è dato da

${\displaystyle {\mathcal {P}}={\sqrt {(x_{A}-x_{B})^{2}+(y_{A}-y_{B})^{2}}}+{\sqrt {(x_{A}-x_{C})^{2}+(y_{A}-y_{C})^{2}}}+{\sqrt {(x_{B}-x_{C})^{2}+(y_{B}-y_{C})^{2}}}.}$

Geometrie non euclidee

Il concetto di triangolo si estende ed è ampiamente usato in tutte le geometrie non euclidee. Un triangolo in una geometria non euclidea si differenzia generalmente per il fatto che la somma dei suoi angoli interni non è 180°: questa somma è inferiore a 180° per ogni triangolo nel caso di una geometria iperbolica, mentre è superiore per ogni triangolo nel caso di una geometria ellittica.

Teoremi sui triangoli

I criterio di congruenza dei triangoli

Se due triangoli hanno rispettivamente congruenti due lati e l'angolo tra essi compreso, essi sono congruenti.

II criterio di congruenza dei triangoli

Se due triangoli hanno rispettivamente congruenti due angoli e il lato ad essi adiacente, essi sono congruenti.

III criterio di congruenza dei triangoli

Se due triangoli hanno rispettivamente congruente i tre lati, essi sono congruenti. Criterio generale di congruenza dei triangoli Se due triangoli hanno rispettivamente congruenti un lato e due angoli qualsiasi, essi sono congruenti.

I teorema dell'angolo esterno

In un triangolo ogni angolo esterno è maggiore di ciascuno degli angoli interni non adiacenti ad esso.

II teorema dell'angolo esterno

In un triangolo l'angolo esterno di uno di essi è uguale alla somma degli altri due angoli interni.

Corollario 1: un triangolo non può avere né due angoli retti, né due angoli ottusi, né un angolo retto e uno ottuso, cioè un triangolo ha almeno due angoli acuti.

Corollario 2: gli angoli alla base di un triangolo isoscele sono acuti.

Disuguaglianza triangolare

In un triangolo ciascun lato è minore della somma degli altri due e maggiore della loro differenza.

I criterio di similitudine dei triangoli

Se due triangoli hanno due angoli rispettivamente congruenti, allora sono simili.

II criterio di similitudine dei triangoli

Se due triangoli hanno rispettivamente due lati proporzionali e l'angolo tra essi compreso congruente, allora sono simili.

III criterio di similitudine dei triangoli

Se due triangoli hanno i tre lati rispettivamente proporzionali, allora sono simili.

I teorema di Euclide

In un triangolo rettangolo ogni cateto è medio proporzionale tra l'ipotenusa e la sua proiezione sull'ipotenusa.

II teorema di Euclide

In un triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale fra le proiezioni dei cateti sull'ipotenusa.

Teorema di Pitagora

In ogni triangolo rettangolo, il quadrato costruito sull'ipotenusa è uguale alla somma dei quadrati costruiti sui cateti.

Note

1. Al libro Topologia di Marco Manetti (2014) viene fatta risalire la tradizione di definire scaleno un triangolo di cui non venga specificata la relazione tra i lati. Questo è diverso dal chiedere che i lati siano tutti diversi. Nella nuova terminologia infatti un triangolo isoscele verrà considerato scaleno.Tale definizione viene ritenuta preferibile a quella tradizionale da molti autori contemporanei.^{[senza fonte]}

Voci correlate

• Encyclopedia of Triangle Centers
• Triangolo di Reuleaux
• Teorema di Pitagora
• Trigonometria

Altri progetti

Altri progetti

• Wikiquote
• Wikizionario
• Wikimedia Commons

• Wikiquote contiene citazioni sul triangolo
• Wikizionario contiene il lemma di dizionario «triangolo»
• Wikimedia Commons contiene immagini o altri file su triangolo

Collegamenti esterni

• triangolo, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• triangolo, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) triangle, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Triangolo, su MathWorld, Wolfram Research.
• Studio dei casi per la risoluzione di un triangolo, su cnuto.it.
• (EN) Triangle in MacTutor
• (EN) Triangle Calculator - completes triangles when given three elements (sides, angles, area, height etc.), supports degrees, radians and grades.
• (EN) Napoleon's theorem A triangle with three equilateral triangles. A purely geometric proof. It uses the Fermat point to prove Napoleon's theorem without transformations by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"
• (EN) William Kahan: Miscalculating Area and Angles of a Needle-like Triangle Archiviato il 10 novembre 2006 in Internet Archive..
• (EN) Clark Kimberling: Encyclopedia of triangle centers. Lists some 1600 interesting points associated with any triangle.
• (EN) Christian Obrecht: Eukleides. Software package for creating illustrations of facts about triangles and other theorems in Euclidean geometry.
• (EN) Triangle constructions, remarkable points and lines, and metric relations in a triangle at cut-the-knot
• (EN) Printable Worksheet on Types of Triangles, su kwiznet.com. URL consultato il 23 novembre 2019 (archiviato dall'url originale il 15 dicembre 2018).
• (EN) Compendium Geometry Analytical Geometry of Triangles
• P. Baroncini - R. Manfredi, MultiMath.blu - Geometria, DeAScuola, 2014, ISBN 978-88-538-0567-6

Controllo di autorità	Thesaurus BNCF 38738 · LCCN (EN) sh85137407 · BNF (FR) cb11946969k (data) · J9U (EN, HE) 987007548775205171

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica