Solido di rotazione

In matematica, e in particolare in geometria, un solido di rotazione o di rivoluzione è la figura ottenuta ruotando attorno ad un asse ${\displaystyle n}$ una regione piana ${\displaystyle K}$, sul cui piano giace l'asse stesso.

Un toro

Ad esempio, il toro è ottenuto dalla rotazione di un cerchio attorno ad un asse esterno al cerchio medesimo.

Solidi ottenuti dalla rotazione di trapezoidi

La figura piana che ruota è spesso un trapezoide con la base sull'asse. La sfera ad esempio è il solido di rotazione del semicerchio intorno al diametro; il cilindro è generato dal rettangolo.

Rotazione di una curva

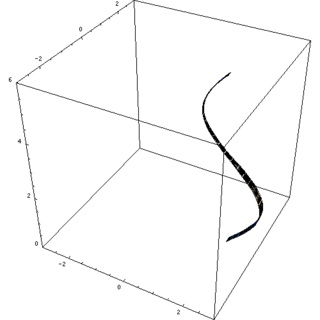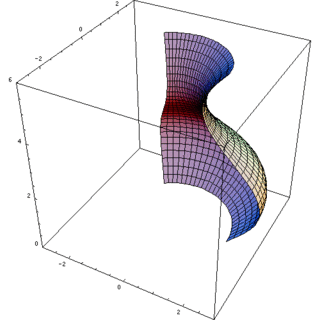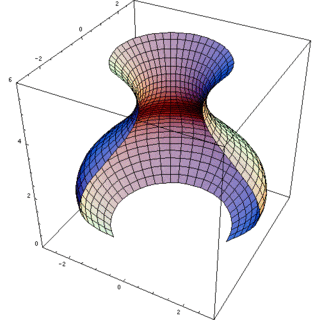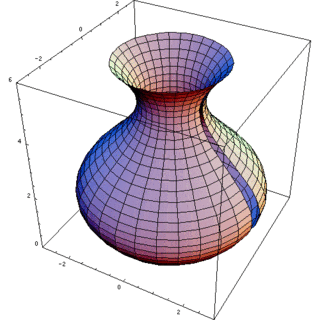
In questo caso il solido è delimitato da una superficie laterale ottenuta ruotando una curva attorno all'asse (superficie di rotazione), ed eventualmente da due basi circolari perpendicolari a tale asse.

Definizione come luogo di punti

A meno di rotazioni dello spazio tridimensionale, l'asse si può considerare coincidente con ${\displaystyle x}$ in modo da poter esprimere il solido in coordinate cilindriche:

${\displaystyle T=\{(x,y,z)\in \mathbb {R} ^{3}|\ a\leq x\leq b\land 0\leq {\sqrt {y^{2}+z^{2}}}\leq f(x)\},}$

dove ${\displaystyle a}$ e ${\displaystyle b}$ sono due valori reali con ${\displaystyle a<b}$, la funzione ${\displaystyle \rho =\rho (y,z)={\sqrt {y^{2}+z^{2}}}}$ è il raggio del cilindro di asse ${\displaystyle x}$ e la funzione ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ è una funzione non negativa e continua, il cui grafico è la curva della definizione che giace sul piano ${\displaystyle xy}$.

Volume e superficie

Lo stesso argomento in dettaglio: Teoremi di Pappo-Guldino.

Il volume ${\displaystyle V}$ del solido ${\displaystyle T}$ si può ottenere idealmente "tagliandolo" in dischi di spessore "infinitesimo" ${\displaystyle dx}$ lungo l'asse ${\displaystyle x}$ (teorema di Fubini). Il disco corrispondente a ${\displaystyle x}$ ha volume uguale all'area del cerchio di raggio ${\displaystyle f(x)}$ moltiplicata per lo spessore ${\displaystyle dx}$. Quindi sommando i vari contributi infinitesimi ${\displaystyle dx}$ (ovvero integrando) si ha

${\displaystyle V=\int _{a}^{b}\pi f(x)^{2}\,dx.}$

La superficie è invece data da:

${\displaystyle A=2\pi \int _{a}^{b}f(x){\sqrt {1+f'(x)^{2}}}\,dx.}$

Se il solido è dato da

${\displaystyle T=\{(x,y,z)\in \mathbb {R} ^{3}|\ a\leq x\leq b\land 0\leq g(x)\leq {\sqrt {y^{2}+z^{2}}}\leq f(x)\},}$

cioè la figura da ruotare è compresa tra due funzioni non negative, allora il volume è

${\displaystyle V=\int _{a}^{b}\pi \left(f(x)^{2}-g(x)^{2}\right)dx.}$

Il volume del solido, se ottenuto tramite rotazione rispetto all'asse ${\displaystyle y}$, con ${\displaystyle a>0}$, si può calcolare pensandolo come la somma delle superfici laterali dei cilindri di asse ${\displaystyle y}$, raggio ${\displaystyle x}$ e altezza ${\displaystyle f(x)}$. Quindi sommando rispetto a ${\displaystyle dx}$ (cioè integrando), si ha:

${\displaystyle V=2\pi \int _{a}^{b}xf(x)\,dx.}$

Nel caso la figura da ruotare sia compresa tra due funzioni, allora si ha:

${\displaystyle V=2\pi \int _{a}^{b}x\vert f(x)-g(x)\vert \,dx.}$

Voci correlate

• Cilindroide
• Integrale multiplo
• Teoria della misura

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su solido di rotazione

Collegamenti esterni

• (EN) Eric W. Weisstein, Solid of Revolution, su MathWorld, Wolfram Research.

Controllo di autorità	Thesaurus BNCF 30687 · GND (DE) 4136951-8

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica