Funzione sigma

La funzione ${\displaystyle \sigma \left(n\right)}$ è una funzione aritmetica, definita come la somma di tutti i divisori positivi di un numero naturale ${\displaystyle n}$:

${\displaystyle \sigma \left(n\right)=\sum _{d|n}d.}$

I primi 250 valori della funzione σ

La funzione sigma generalizzata è invece definita come la somma delle ${\displaystyle \alpha }$-esime potenze dei divisori di ${\displaystyle n}$:

${\displaystyle \sigma _{\alpha }\left(n\right)=\sum _{d|n}d^{\alpha }.}$

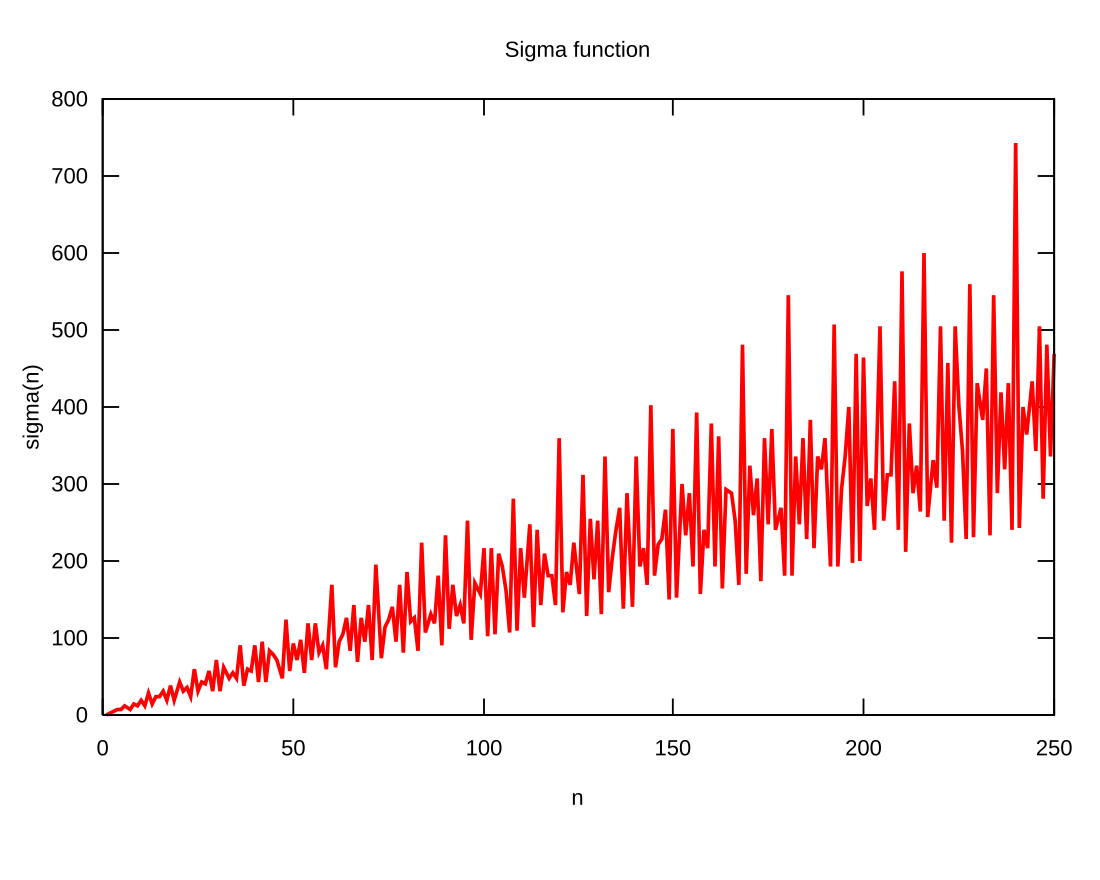
Valori della funzione

Per ${\displaystyle n\geq 2}$, il valore di ${\displaystyle \sigma (n)}$ è sempre maggiore o uguale del numero ${\displaystyle n}$ stesso più ${\displaystyle 1}$, perché ogni numero e ${\displaystyle 1}$ sono divisori del numero stesso: si ha ${\displaystyle \sigma (n)\geq n+1}$, con l'uguaglianza se e solo se ${\displaystyle n}$ è un numero primo. Se invece ${\displaystyle n}$ è composto, vale la disuguaglianza più forte ${\displaystyle \sigma (n)\geq n+{\sqrt {n}}+1}$.

n	1	2	3	4	5	6	7	8	9	10
σ(n)	1	3	4	7	6	12	8	15	13	18
n	11	12	13	14	15	16	17	18	19	20
σ(n)	12	28	14	24	24	31	18	39	20	42

Proprietà

La funzione sigma è una funzione moltiplicativa, ma non completamente moltiplicativa; da questo si può ricavare una formula compatta per il calcolo di questa funzione. Sia ${\displaystyle n=p_{1}^{q_{1}}p_{2}^{q_{2}}\cdots p_{k}^{q_{k}}}$.

${\displaystyle \sigma (p_{i}^{q_{i}})=1+p_{i}+p_{i}^{2}+p_{i}^{3}+\cdots +p_{i}^{q_{i}}={\frac {p_{i}^{q_{i}+1}-1}{p_{i}-1}},}$

essendo una serie geometrica, e quindi

${\displaystyle \sigma (n)={\frac {p_{1}^{q_{1}+1}-1}{p_{1}-1}}{\frac {p_{2}^{q_{2}+1}-1}{p_{2}-1}}\cdots {\frac {p_{k}^{q_{k}+1}-1}{p_{k}-1}}=\prod _{i=1}^{k}{\frac {p_{i}^{q_{i}+1}-1}{p_{i}-1}}.}$

Soddisfa l'identità

${\displaystyle \sigma _{\alpha }\left(n\right)=\prod _{p^{m}|n}{\frac {p^{\alpha \left(m+1\right)}-1}{p^{\alpha }-1}}.}$

Altre due notevoli identità che riguardano la funzione sigma sono

${\displaystyle -\sum _{n=1}^{\infty }\ln \left(1-x^{n}\right)=\sum _{n=1}^{\infty }\sigma _{-1}\left(n\right)x^{n},}$

e

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{\alpha }\left(n\right)}{n^{s}}}=\zeta \left(s\right)\zeta \left(s-\alpha \right),}$

dove ${\displaystyle \zeta \left(s\right)}$ è la funzione zeta di Riemann.

La funzione ${\displaystyle \sigma _{0}(n)}$ è anche nota come funzione tau.

Casi particolari

La funzione sigma generalizzata con ${\displaystyle \alpha =0}$, ${\displaystyle \sigma _{0}(n)}$ restituisce il numero totale di divisori di ${\displaystyle n}$. Sia n scomponibile in fattori primi come ${\displaystyle n=p_{1}^{q_{1}}p_{2}^{q_{2}}\cdots p_{k}^{q_{k}}}$, allora

${\displaystyle \sigma _{0}(n)=\prod _{i=1}^{k}(q_{i}+1).}$

Ad esempio, il numero di divisori del numero ${\displaystyle 24=2^{3}\cdot 3}$ possono essere calcolati come

${\displaystyle \sigma _{0}(24)=\prod _{i=1}^{2}(q_{i}+1)=(3+1)\cdot (1+1)=8.}$

In effetti il numero 24 ha 8 divisori (1, 2, 4, 8, 3, 6, 12 e 24).

Codice

In C:

int sigma( int N ){//la funzione riceve un intero naturale N e restituisce la somma dei suoi divisori
	int i, res=0;
	if (N<1) return 0;//se N è non positivo, restituisce zero
	for (i=1; i<=N; i++)
		if( !(N%i) ) // equivalente a (N%i)==0
			res+=i;
	return res;
}

Voci correlate

• Funzione tau sui positivi

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sulla funzione sigma

Collegamenti esterni

• (EN) Eric W. Weisstein, Divisor Function, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica