Էլիպս

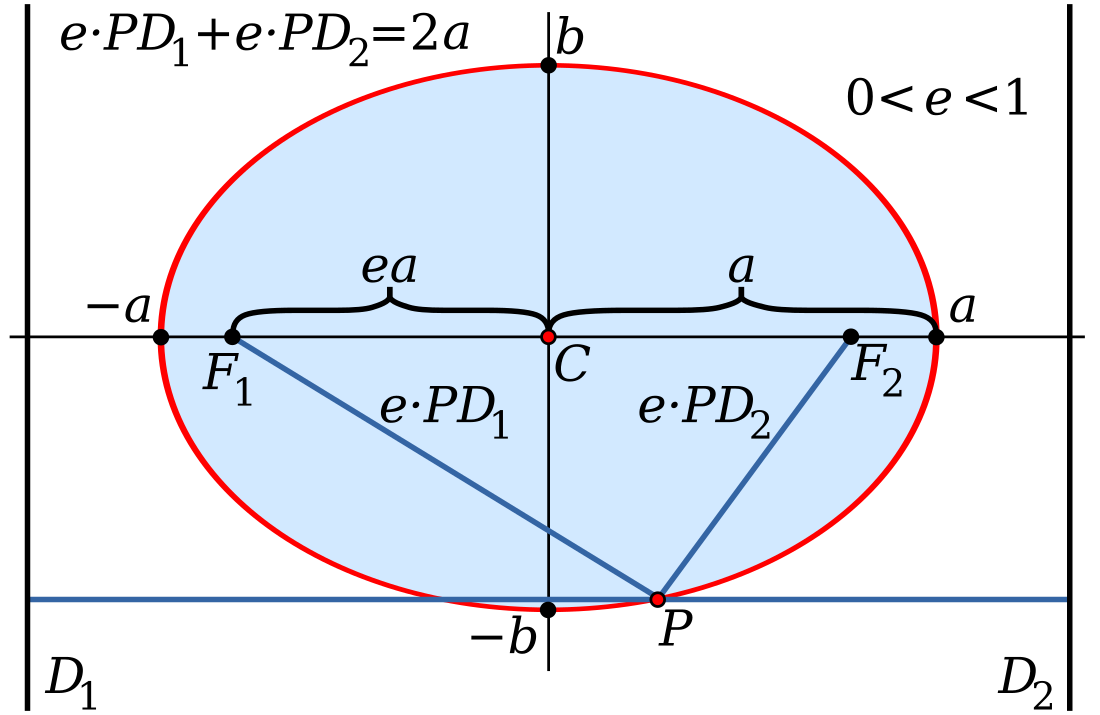
Ձվածիրը, կամ Էլիպսը երկրաչափական պատկեր է։ Էլիպս է կոչվում հարթության այն կետերի երկրաչափական տեղը, որոնց հեռավորությունների գումարը տրված երկու
${\displaystyle F1}$ և ${\displaystyle F2}$ կետերից հաստատուն է և մեծ է ${\displaystyle F_{1}F_{2}}$ հատվածի երկարությունից։Այդ հաստատունը կնշանակենք 2a-ով։ ${\displaystyle F1}$-ը և ${\displaystyle F2}$-ը կոչվում են էլիպսի ֆոկուսներ, իսկ ${\displaystyle F_{1}F_{2}}$ հատվածի երկարությունը կնշանակենք 2c-ով, և կանվանենք ֆոկուսային հեռավորություն։

Անվան այլ կիրառումների համար տե՛ս՝ Էլիպս (այլ կիրառումներ)

Էլիպսի հավասարումը

Հարթության վրա ուղղանկյուն կոորդինատային համակարգն ընտրենք այնպես, որ Ox առանցքն անցնի ${\displaystyle F_{1}}$ և ${\displaystyle F_{2}}$ կետերով, իսկ Oy առանցքը՝ ${\displaystyle F_{1}F_{2}}$ հատվածի միջնակետով։ Այս դեպքում, ըստ սահմանման, էլիպսի ցանկացած P(x, y) կետի համար՝

P${\displaystyle F_{1}}$ + P${\displaystyle F_{2}}$ = 2a

Հաշվի առնելով, որ ${\displaystyle F_{1}}$ կետի կոորդինատներն են ${\displaystyle F_{1}}$(-c;0) , իսկ ${\displaystyle F_{2}}$ կետինը ${\displaystyle F_{1}}$(c;0), երկու կետի հեռավորության բանաձևից ստանում ենք՝

${\displaystyle {\sqrt {(x+c)^{2}+y^{2}}}+{\sqrt {(x-c)^{2}+y^{2}}}=2a}$

Սա էլ հենց հանդիսանում է էլիպսի հավասարումը ընտրված կոորդինատային համակարգում։ Փորձենք այն գրել կոմպակտ տեսքով։ Դրա համար երկրորդ գումարելին տեղափոխենք հավասարման աջ մաս և երկու կողմերը բարձրացնենք քառակուսի՝

${\displaystyle ~(x+c)^{2}+y^{2}=4a^{2}-4a{\sqrt {(x-c)^{2}+y^{2}}}+(x-c)^{2}+y^{2}}$

Պարզեցումներից հետո ստանում ենք՝

${\displaystyle ~(a^{2}-c^{2})x^{2}+a^{2}y^{2}=a^{2}(a^{2}-c^{2})}$

Քանի որ ${\displaystyle ~a>c}$, ապա ${\displaystyle ~a^{2}-c^{2}}$ > 0 ։ Նշանակենք ${\displaystyle ~b^{2}=a^{2}-c^{2}}$, ուստի ${\displaystyle b={\sqrt {a^{2}-c^{2}}}}$ հետևաբար հավասարումը կընդունի հետևյալ տեսքը՝

${\displaystyle ~b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}}$

կամ

${\displaystyle ~{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

որը կոչվում է էլիպսի կանոնական հավասարում ։ Այստեղ 2a-ն և 2b-ն կոչում են էլիպսի համապատասխանաբար մեծ և փոքր առանցքների երկարություններ, իսկ կոորդինատների սկզբնակետը՝ էլիպսի կենտրոն։ ${\displaystyle e={\frac {c}{a}}}$ թիվը կոչվում է էլիպսի էքսցենտրիսիտետ ։ Կոորդինատային առանցքների հետ հատման կետերը կոչվում են էլիպսի գագաթներ։

Դիտողություն

Նշենք, որ իրականում մենք ցույց տվեցինք, որ(1) հավասարմանը բավարարող ցանկացած M(x;y) բավարարում է նաև (2) հավասարմանը։ Կարելի է ցույց տալ, որ ճիշտ է նաև հակառակը, այսինքն (2)-ին բավարարող ցանկացած M(x;y) կետ բավարարում է նաև (1)-ին։ Օրինակ։ Գտնել հետևյալ հավասարումով տրված էլիպսի ֆոկուսների հեռավորությունը և էքսցենտրիսիտետը։

${\displaystyle ~3x^{2}+4y^{2}=5}$

Լուծում

հավասարման երկու մասը բաժանելով 5-ի՝ ստանում ենք

${\displaystyle {\frac {x^{2}}{\frac {5}{3}}}+{\frac {y^{2}}{\frac {5}{4}}}=1}$

ուստի ${\displaystyle a={\sqrt {\frac {5}{3}}}}$; ${\displaystyle b={\sqrt {\frac {5}{4}}}}$ ${\displaystyle ~{c^{2}}={a^{2}}-{b^{2}}={\frac {5}{3}}-{\frac {5}{4}}={\frac {5}{12}}}$ ,${\displaystyle ~2c=2{\sqrt {\frac {5}{12}}}}$ ${\displaystyle e={\sqrt {\frac {5}{12}}}:{\sqrt {\frac {5}{3}}}}$ = ${\displaystyle {\frac {1}{2}}}$ 001

Գրականություն

• Ի․ Պրիվալով "Անալիտիկ երկրաչափություն" Գրքի օնլայն տարբերակը Արխիվացված 2021-08-13 Wayback Machine

Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից  (հ․ 4, էջ 36)։