A statisztikai hipotézisvizsgálatban egy eredmény akkor mondható statisztikailag szignifikánsnak, ha ez a nullhipotézis mellett nagyon valószínűtlen lenne. Vagyis egy tanulmány előre meghatározott szignifikanciaszintje (jele: α) annak a valószínűsége, hogy a tanulmány elutasítja a nullhipotézist, azt feltételezve, hogy az igaz; egy eredmény p-értéke (p) annak a valószínűsége, hogy egy legalább olyan kiugró eredményt kapjunk, ugyancsak azt feltételezve, hogy a nullhipotézis igaz. Az eredmény akkor statisztikailag szignifikáns a tanulmány feltételei mellett, ha p ≤ α. Egy tanulmány szignifikanciaszintjét az adatgyűjtés előtt határozzák meg, és általában 5%-ra teszik, vagy ennél sokkal alacsonyabbra, tudományterülettől függően.
| Ez a szócikk nem tünteti fel a független forrásokat, amelyeket felhasználtak a készítése során. Emiatt nem tudjuk közvetlenül ellenőrizni, hogy a szócikkben szereplő állítások helytállóak-e. Segíts megbízható forrásokat találni az állításokhoz! Lásd még: A Wikipédia nem az első közlés helye. |
Bármilyen kísérletben vagy megfigyelésben, ami egy populációból vett mintát vizsgál, benne van a lehetőség, hogy a megfigyelt (nem nulla mértékű) hatás csak a mintavételi hiba miatt következett be. De ha a hatás p-értéke kisebb vagy egyenlő a szignifikanciaszinttel, akkor a kutató azt a következtetést vonhatja le, hogy ez a hatás az egész populációra igaz, vagyis elutasíthatja a nullhipotézist.
A statisztikai szignifikanciatesztelés ezen módszerét a 20. században fejlesztették ki. A szignifikancia kifejezés esetünkben nem a fontosságot jelenti, valamint a statisztikai szignifikancia nem egyenlő a kutatási, elméleti és gyakorlati szignifikanciával.
A statisztikai szignifikancia fogalma az 1700-as évekre vezethető vissza, John Arbuthnot és Pierre-Simon Laplace munkásságára, akik kiszámolták embereknél a születési nemi arányok p-értékét, nullhipotézisként feltételezve, hogy ugyanakkora eséllyel születnek fiúk és lányok.
1925-ben Ronald Fisher bevezette a statisztikai hipotézisvizsgálat elképzelését, amit ő „a szignifikancia tesztjének” hívott a Statistical Methods for Research Workers c. könyvében. Fisher egy a húszhoz (0,05) arányló valószínűséget javasolt, amit egy megfelelő szintnek tartott a nullhipotézis elutasítására. Egy 1933-as cikkükben Jerzy Neyman és Egon Pearson ezt a szintet szignifikanciaszintnek hívták, amit α-nak neveztek. Emellett azt is előterjesztették, hogy a szignifikanciaszintet a kutatók az adatgyűjtés előtt határozzák meg.
Annak ellenére, hogy Fisher javasolt egy értéket a szignifikanciaszintnek, nem gondolta, hogy ennek az értéknek fixnek kellene lennie. Az 1956-os Statisztikai módszerek és tudományos következtetések c. publikációjában azt javasolta, hogy a szignifikanciaszintet mindig az aktuális körülményekhez képest határozzák meg.
Kapcsolódó fogalmak
Az α az a küszöbérték, ami alatti p-értéket kapva, a nullhipotézis elutasításra kerül, annak ellenére, hogy alapvető feltételezésként igaznak tartjuk. Ez azt jelenti, hogy α annak a valószínűsége is, hogy elutasítjuk a nullhipotézist, amikor az igaz. Ezt hívják fals pozitív, vagy elsőfajú hibának is.
Néha a kutatók inkább konfidenciaszintet használnak: γ = (1 – α). Ez annak a valószínűsége, hogyha a vizsgálat alapján a nullhipotézis igaznak bizonyul, akkor azt nem utasítjuk el. A konfidenciaszinteket és konfidenciaintervallumok fogalmát Neyman vezette be 1937-ben.
A statisztikai szignifikancia kulcsszerepet játszik a statisztikai hipotézisvizsgálatokban, mivel ezt használják annak a meghatározására, hogy a nullhipotézis elutasításra kerül-e, vagy sem. A nullhipotézis az alapvető feltételezés, miszerint semmi sem történt vagy változott. Ahhoz, hogy a nullhipotézist elutasítsuk, a megfigyelt eredménynek statisztikailag szignifikánsnak kell lennie, vagyis a megfigyelt p-értéknek kisebbnek kell lennie, mint az előre meghatározott α szignifikanciaszint.
Ahhoz, hogy egy kutató megállapítsa az eredményeiről, hogy azok statisztikailag szignifikánsak-e, ki kell számolnia a p-értéket, ami annak a valószínűsége, hogy ugyanolyan, vagy még nagyobb mértékű hatás mérhető, azt feltételezve, hogy a nullhipotézis igaz. A nullhipotézis akkor kerül elutasításra, ha a p-érték kisebb (vagy egyenlő), mint az előre meghatározott α-szint. Az α egyben annak a valószínűsége is, hogy a nullhipotézis elutasításra kerül, miközben az valójában igaz (elsőfajú hiba). Általában 5%-nál vagy alatta húzzák meg.
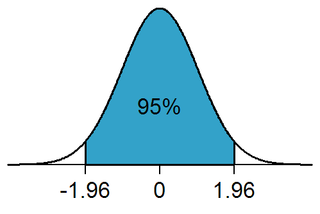
Például, ha α-t 5%-nál határozzák meg, a feltételes valószínűsége annak, hogy elsőfajú hibát követünk el (feltételezve, hogy a nullhipotézis igaz), 5%, és az számít statisztikailag szignifikáns eredménynek, ha a p-érték kisebb vagy egyenlő, mint 5%. Ez azt jelenti, hogy amikor egy populációból veszünk mintát, az elutasítási régió az 5%-a a mintavételi eloszlásnak. Ez az 5% kerülhet az egyik oldalára az eloszlásnak az egyoldalas próbák esetén, vagy elosztódhat mindkét oldalra egy kétoldalas próba esetén, ahol az eloszlás mindkét „farka” (elutasítási régiója) 2,5%-nyi területet foglal magába.
Az egyoldalas próba attól függően kerül használatra, hogy a kutatási kérdés vagy az alternatív hipotézis meghatároz-e egy irányt, mint például egy adott tárgycsoport nehezebb-e, vagy a diákok teljesítménye egy felmérésen jobb-e. Ilyenkor is lehet használni kétoldalas próbát, azonban gyengébb lesz, mint az egyoldalas, mert az egyoldalas próbák elutasítási régiója az eloszlás egyik végére koncentrálódik csak, és kétszer akkora (5% vs. 2,5%), mint a kétoldalas próbák bármelyik elutasítási régiója. Ennek eredményeként a nullhipotézis elutasításra kerülhet egy kevésbé kiugró eredménynél is, ha egyoldalas próbát használtak a kutatók. Az egyoldalas próba csak akkor erősebb, mint a kétoldali, ha a meghatározott irány, illetve az alternatív hipotézis helyes.
Szignifikanciaszintek különböző területeken
Bizonyos területeken, mint a részecskefizika vagy a gyártásipar a statisztikai szignifikanciát sokszor a szórás vagy a szigma (σ) sokszorosaként fejezik ki, a szignifikanciaszintek itt jóval szigorúbbak (pl. 5σ). Példaként: annak a bizonyosságát, hogy a Higgs-bozon részecske valóban létezik, az 5σ határértékhez képest határozták meg, ami nagyjából 1 a 3,5 millióhoz való p-érték aránynak felel meg.
Más tudományterületeken, mint például a teljes genom asszociációs vizsgálatokban a szignifikanciaszintek elérhetik az 5 ∙ 10-8 szintet is, mivel a vizsgálatok száma rendkívül nagy.
Azok a kutatók, akik csupán a statisztikai szignifikanciára támaszkodnak, abba a csapdába eshetnek, hogy olyan eredményeket közölnek, amelyek nem valósak vagy nem megismételhetők. Meg kell különböztetnünk emellett statisztikai és gyakorlati szignifikanciát is – attól még, hogy egy eredmény statisztikailag szignifikáns, nem feltétlenül jelenti, hogy a gyakorlatban is fontos.
Hatásméret
A hatásméret egy vizsgálat gyakorlati szignifikanciáját (fontosságát) méri. Egy statisztikailag szignifikáns eredmény lehet kis hatásméretű. Ahhoz, hogy meg lehessen becsülni egy eredmény tudományos szignifikanciáját, a kutatóknak ajánlott közölni a hatásméretet is a p-értékkel együtt. A hatásméret számszerűsítésére több mód is van, mint például két átlag különbségének és a (közös) szórásnak a hányadosaként (vö. Cohen-féle delta), a korrelációs koefficiensként két változó között, ennek a négyzeteként, és más mértékegységekként.
Megismételhetőség
Bizonyos statisztikailag szignifikáns eredményeket nem egyszerű megismételni, ezek gyakran fals pozitív eredmények – minden olyan kísérlet, ahol egy eredményt nem sikerül megismételni, megerősíti annak a valószínűségét, hogy az eredeti eredmény egy hamis pozitív eredmény volt.
Túlzott használat folyóiratokban
A 2010-es években bizonyos folyóiratok elkezdték megkérdőjelezni a szignifikanciatesztek elsődlegességét egy hipotézis érvényességének megállapításában, különösen az α = 5%-os küszöböt. Ezek a folyóiratok arra késztették a kutatókat, hogy egyetlen szignifikanciatesztnél részletesebb elemzéseket végezzenek. A szociálpszichológiában a Basic and Applied Social Psychology c. folyóirat teljesen megtiltotta a szignifikanciatesztelést azokban a cikkekben, amiket publikált, arra kényszerítve a kutatókat, hogy más eszközökkel mérjék fel a hipotéziseik validitását.
Más szerkesztők ezzel a tiltással kapcsolatban megjegyezték, hogy „a p-értékek közlésének betiltása, ahogy a Basic and Applied Social Psychology tette, nem a problémát oldja meg, csupán egy tünetét kezeli. Nincsen semmi probléma a hipotézisvizsgálatokkal és p-értékekkel, amíg a cikkek szerzői, bírálói és szerkesztői megfelelően használják őket.” Bizonyos statisztikusok eltérő mérőeszközöket részesítenek előnyben, mint például valószínűségi arányokat vagy Bayes-faktorokat. A bayesiánus statisztikával meg lehet kerülni a konfidenciaszinteket, ugyanakkor további előfeltevéseket kíván, és így nem feltétlenül javít a statisztikai vizsgálatok hibás gyakorlatán.
A széleskörű visszaélés a statisztikai szignifikanciával egy fontos metatudományos kutatási téma.
A szignifikancia újraértelmezése
2016-ban az Amerikai Statisztikai Társaság (ASA) így nyilatkozott a p-értékekről: „a statisztikai szignifikancia széleskörű használata (általánosan p ≤ 0,05-ként értelmezve) mint feljogosítás arra, hogy a kutatók azt állítsák, hogy új eredményt találtak, a tudományos eljárás jelentős torzulásához vezet.” 2017-ben 72 szerző felvetette, hogy a megismételhetőség érdekében a p-érték szignifikanciaszintjét 0,05-ról 0,005-re kellene csökkenteni. Más kutatók erre a felvetésre azzal válaszoltak, hogy a szigorúbb szignifikanciaszintek csak felerősítenének más problémákat, mint pl. az adatkotrás. Alternatív felvetések között szerepel a rugalmasabb (indokolt) p-érték meghatározása adatgyűjtés előtt az egyes vizsgálatoknál, illetve a p-értékek folyamatos indexekként való értelmezése, ezáltal elhagyva a küszöbértékeket és a statisztikai szignifikanciát. Emellett a küszöbérték 0,005-re változtatása megnövelné a hamis negatív eredmények valószínűségét, mely esetben a vizsgált hatás valós, de statisztikailag nem kimutatható.
2019-ben több mint 800 statisztikus és kutató írt alá egy üzenetet, amelyben a „statisztikai szignifikancia” fogalom elhagyását követelték a tudományban.
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.