Robinson-vetület
egyfajta világtérkép From Wikipedia, the free encyclopedia
A Robinson-vetület egy pszeudo-hengeres térképábrázolási módszer, amivel a gömb alakú Föld egyetlen felületen, síkban ábrázolható. A torzítások mértékében (terület, szög, alak) egyfajta kompromisszumot jelent más vetületekkel szemben.[1]
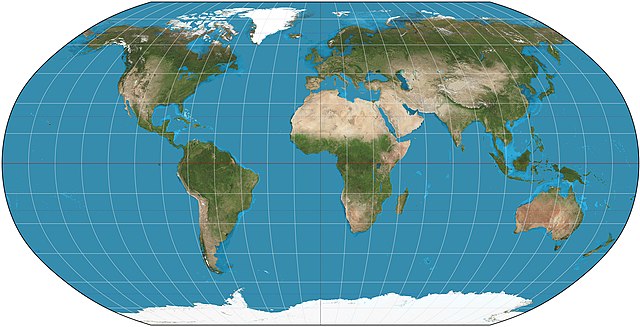
A vetületet Arthur H. Robinson hozta létre 1963-ban a Rand McNally társaság kérésére, akik azóta az így készült világtérképeket általános célra forgalmazták. Robinson a vetület előállításának részleteit 1974-ben publikálta. A National Geographic Society (NGS) 1988-ban kezdte használni a vetületet az általa készített világtérképeken, amiken 1922 és 1988 között a Van der Grinten I vetületet alkalmazták (az NGS az emblémáján is ez utóbbit jelenítette meg).[2]
1998-ban a National Geographic Society abbahagyta a Robinson-vetület alkalmazását, és a „Winkel tripel projekciót (Winkel III)” kezdte használni, mert az a sarkoknál kevésbé torzít.[3][4]
Előnyök, hátrányok
A Robinson-vetület sem nem egyenlő területű, sem nem konform leképezésű, mindkettőnél kompromisszumot köt. Robinson úgy gondolta, hogy ezzel a módszerrel a térkép jobban néz ki, mint ha valamelyik kritériumhoz mereven ragaszkodott volna. A délkörök ívesek, a sarkok azonban vonalakká torzulnak pontok helyett.[1] A sarkoknál tehát jelentős a torzítás, de kisebb szélességi köröknél ez gyorsan elfogadható mértékűre csökken. A párhuzamos vonalak komoly szögtorzulást szenvednek nagy szélességeknél, a térkép szélei felé, de ez mindegyik pszeudo-hengeres vetület sajátossága. A bevezetése idején azonban a vetület megfelelt a Rand McNally céljainak, ami a világtérkép tetszetős ábrázolása volt.[5][6]
Előállítása
A vetületet az alábbi táblázat határozza meg.
| Szélesség | PLEN | PDFE |
|---|---|---|
| 00 | 1,0000 | 0,0000 |
| 05 | 0,9986 | 0,0620 |
| 10 | 0,9954 | 0,1240 |
| 15 | 0,9900 | 0,1860 |
| 20 | 0,9822 | 0,2480 |
| 25 | 0,9730 | 0,3100 |
| 30 | 0,9600 | 0,3720 |
| 35 | 0,9427 | 0,4340 |
| 40 | 0,9216 | 0,4958 |
| 45 | 0,8962 | 0,5571 |
| 50 | 0,8679 | 0,6176 |
| 55 | 0,8350 | 0,6769 |
| 60 | 0,7986 | 0,7346 |
| 65 | 0,7597 | 0,7903 |
| 70 | 0,7186 | 0,8435 |
| 75 | 0,6732 | 0,8936 |
| 80 | 0,6213 | 0,9394 |
| 85 | 0,5722 | 0,9761 |
| 90 | 0,5322 | 1,0000 |
A táblázat a földrajzi szélesség értékei szerint van megadva. A PLEN oszlop a szélességi kör hossza, a PDFE oszlop a szélességi kör távolságát adja meg az egyenlítőtől. A hosszúsági körök egyenlő távolságra vannak egymástól minden szélességi körön.
Források
- Norman Thrower: Maps and Civilization, The University of Chicago Press, 2008, ISBN 0-226-79974-3
Kapcsolódó szócikkek
További információk
- Arthur H. Robinson (1974). A New Map Projection: Its Development and Characteristics. In: „International Yearbook of Cartography”. Vol 14, 1974, pp. 145–155.
- John B. Garver Jr. (1988). New Perspective on the World. In: National Geographic, December 1988, pp. 911–913.
- John P. Snyder (1993). Flattening The Earth—2000 Years of Map Projections, The University of Chicago Press. pp. 214–216.
- Table of examples and properties of all common projections, from radicalcartography.net
- An interactive Java Applet to study the metric deformations of the Robinson Projection.
- Numerical evaluation of the Robinson projection, from Cartography and Geographic Information Science, April, 2004 by Cengizhan Ipbuker
Fordítás
- Ez a szócikk részben vagy egészben a Robinson projection című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
Wikiwand - on
Seamless Wikipedia browsing. On steroids.