Trapézszabály

A matematikában a trapézszabály közelítő eljárás határozott integrálok meghatározására, melynek során egy függvénygörbe meghatározott intervallumba eső görbe alatti területét egy, a görbe által meghatározott trapéz területével helyettesíti. Infinitezimális változata, melynek során az intervallum felosztása minden határon túl finomodik, egy konkrét (nem közelítő) algoritmust jelent a határozott integrálok meghatározására.

${\displaystyle \int \limits _{a}^{b}f(x)\,dx.}$

A kék f(x) függvényt a piros lineáris függvény közelíti.

Húrtrapézformula

Húrtrapéz

Itt a két végpontot összekötő húr alatti trapézzal helyettesítjük a görbe alatti területet:

${\displaystyle \int _{a}^{b}f(x)\,dx\approx (b-a){\frac {f(b)+f(a)}{2}}}$

Ha ${\displaystyle f}$ második deriváltja folytonos ${\displaystyle [a,b]}$-n, akkor

${\displaystyle \left|\int _{a}^{b}f(x)\,dx-(b-a){\frac {f(b)-f(a)}{2}}\right|\leq {\frac {(b-a)^{3}}{12}}\max _{a\leq x\leq b}\left|f''(x)\right|.}$

Összetett húrtrapézformula

Összetett trapézformula

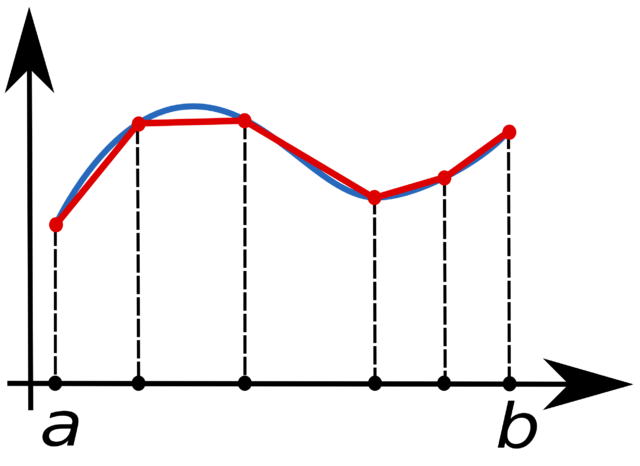
Hogy a közelítést pontosabbá tegyük, az integrálási ${\displaystyle [a,b]}$ tartományt ${\displaystyle N}$ kisebb, diszjunkt részintervallumokra bontjuk;

Legyen f értéke ${\displaystyle x_{1},\ldots ,x_{N}}$ helyeken rendre ${\displaystyle y_{1},\ldots ,y_{N}}$, ekkor az integrál a következőképpen közelíthető:

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {1}{2}}\sum _{i=2}^{N}(x_{i}-x_{i-1})(y_{i}+y_{i-1}),}$

speciálisan, ha a részintervallumok egyenlő hosszúak:

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{N}}\sum _{i=1}^{N}{\frac {1}{2}}(f(a+i{\frac {N}{b-a}})+f(a+(i-1){\frac {N}{b-a}})={\frac {b-a}{N}}\left({\frac {f(a)+f(b)}{2}}+\sum _{i=1}^{N-1}f(a+i{\frac {b-a}{N}})\right).}$

Érintőtrapézformula

Érintőtrapéz

Az érintőtrapézformula azzal a trapézzal közelíti a területet, melynek az egyetlen tengelyekkel nem feltétlen párhuzamos oldala tartalmazza az ${\displaystyle f}$ függvény gráfjának ${\displaystyle [a,b]}$ intervallum felezőpontjához tartozó pontját. Így:

${\displaystyle \int _{a}^{b}f(x)\,dx\approx (b-a)f\left({\frac {(b-a)}{2}}\right)}$,

ahol, ha ${\displaystyle f}$ második deriváltja folytonos ${\displaystyle [a,b]}$-n, akkor

${\displaystyle \left|\int _{a}^{b}f(x)\,dx-(b-a)f\left({\frac {(b-a)}{2}}\right)\right|\leq {\frac {(b-a)^{3}}{24}}\max _{a\leq x\leq b}{\left|f''(x)\right|}}$

Algoritmus

A függvény, amit integrálni szeretnénk: ${\displaystyle f(x)=e^{x}}$, a ${\displaystyle [0,5]}$ intervallumon, 10-es felosztással.

import math
def Fx(x):
    return math.exp(x)
def TrapezIntegralas(a,b,n):
    h=(b-a)/n
    x=a
    s=0.0
    for i in range(1,n,1):
        x=x+h
        s=s+Fx(x)
    return h*(s+(Fx(a)+Fx(b))/2)
print 'Trapezintegral:', TrapezIntegralas(0.0,5.0,10)

Az algoritmus a 150.4715 értéket adja vissza, míg a pontos érték a: 147.4131

Kapcsolódó szócikkek

• Darboux-integrál
• Simpson-módszer
• Romberg-módszer
• Newton–Cotes-formula

Jegyzetek

Források

• Trapezium Rule
• Atkinson, Kendall E. (1989), An Introduction to Numerical Analysis (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50023-0.
• Rahman, Qazi I.; Schmeisser, Gerhard (December 1990), "Characterization of the speed of convergence of the trapezoidal rule", Numerische Mathematik 57 (1): 123–138, doi:10.1007/BF01386402, ISSN 0945-3245

Külső hivatkozások

• Trapezoidal Rule for Numerical Integration
• Notes on the convergence of trapezoidal-rule quadrature Archiválva 2021. február 9-i dátummal a Wayback Machine-ben
• Trapezoidal Rule of Integration – Notes, PPT, Videos, Mathcad, Matlab, Mathematica, Maple, Multiple Choice Tests at Holistic Numerical Methods Institute
• C Language Implementation of Trapezoidal Rule