Liouville-függvény

A számelméletben a Liouville-függvény egy fontos számelméleti függvény, amit Joseph Liouville-ről neveztek el. Ha n pozitív egész, akkor λ(n) definíciója:

${\displaystyle \lambda (n)=(-1)^{\Omega (n)},\,\!}$

Az L(n) Liouville-függvény összegzési függvényen = 10⁴-ig. A jól látható oszcilláció a Riemann-féle zéta-függvény első nem triviális gyökére utal

Az L(n) Liouville-függvény összegzési függvénye n = 10⁷-ig. Az oszcillációk skálainvariánsak

ahol a nagy omega függvény n prímosztóinak száma multiplicitással számolva.(A008836 sorozat az OEIS-ben).

λ teljesen multiplikatív, mivel Ω(n) teljesen additív, vagyis Ω(ab) = Ω(a) + Ω(b). Az egynek nincsenek prímosztói, ezért Ω(1) = 0, így λ(1) = 1. A Liouville-függvény eleget tesz a következő azonosságnak:

${\displaystyle \sum _{d|n}\lambda (d)={\begin{cases}1&{\text{ha }}n{\text{ négyzetszám,}}\\0&{\text{egyébként.}}\end{cases}}}$

A Liouville-függvény Dirichlet-inverze a Möbius-függvény abszolútértéke.

Sorok

A Liouville-függvény Dirichlet-sora kapcsolódik a Riemann-féle zéta-függvényhez:

${\displaystyle {\frac {\zeta (2s)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\lambda (n)}{n^{s}}}.}$

Lambert-sora:

${\displaystyle \sum _{n=1}^{\infty }{\frac {\lambda (n)q^{n}}{1-q^{n}}}=\sum _{n=1}^{\infty }q^{n^{2}}={\frac {1}{2}}\left(\vartheta _{3}(q)-1\right),}$

ahol ${\displaystyle \vartheta _{3}(q)}$ a Jacobi-féle thetafüggvény.

Megcáfolt sejtések

Az L(n) Liouville-függvény összegzési függvényének negatívjának grafikonja n = 2 × 10⁹-ig. A zöld vonal mutatja azt a tartományt, ahol a Pólya-sejtés nem teljesül; a kék görbe az első Riemann-féle gyök hozzájárulását mutatja az oszcillációhoz

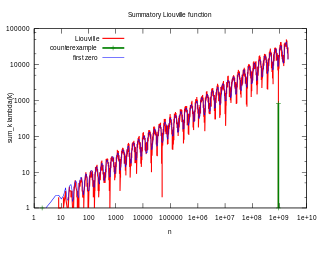
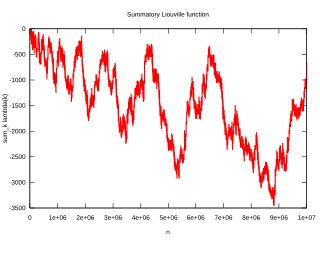
A Pólya-sejtés Pólya Györgytől származik 1919-ből. Legyen

${\displaystyle L(n)=\sum _{k=1}^{n}\lambda (k).}$

A sejtés azt állítja, hogy ${\displaystyle L(n)\leq 0}$ minden n > 1. Ezt azóta megcáfolták. A legkisebb ellenpélda n = 906150257, amit Minoru Tanaka fedezett fel 1980-ban. Azóta megmutatták, hogy L(n) > 0,0618672√n végtelen sok n-re,^[1] míg L(n) < −1,3892783√n végtelen sok pozitív n-re.

A kapcsolódó összeg

${\displaystyle T(n)=\sum _{k=1}^{n}{\frac {\lambda (k)}{k}}.}$

Sokáig nyitott kérdés volt, hogy T(n) ≥ 0 egy elég nagy n ≥ n₀-ra. Ennek felvetését sokszor Turán Pálnak tulajdonítják, tévesen. Ezt Haselgrove cáfolta meg 1958-ban, megmutatva, hogy T(n) végtelen sokszor negatív. Az ellenkező eredmény a Riemann-sejtést is bebizonyította, ahogy Turán Pál levezette.

Jegyzetek

1. P. Borwein, R. Ferguson, and M. J. Mossinghoff, Sign Changes in Sums of the Liouville Function, Mathematics of Computation 77 (2008), no. 263, 1681–1694.

Források

• Polya, G. (1919). „Verschiedene Bemerkungen zur Zahlentheorie”. Jahresbericht der Deutschen Mathematiker-Vereinigung 28, 31–40. o.
• (1958) „A disproof of a conjecture of Polya”. Mathematika 5, 141–145. o. DOI:10.1112/S0025579300001480. ISSN 0025-5793.
• (1960) „On Liouville's function”. Math. Comp. 14, 311–320. o. DOI:10.1090/S0025-5718-1960-0120198-5.
• (1980) „A Numerical Investigation on Cumulative Sum of the Liouville Function”. Tokyo Journal of Mathematics 3 (1), 187-189. o. DOI:10.3836/tjm/1270216093.
• Weisstein, Eric W.: Liouville Function (angol nyelven). Wolfram MathWorld
• Sablon:Springer

Fordítás

• Ez a szócikk részben vagy egészben a Liouville function című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.