समाकलन

यह लेख कलन में निश्चित समाकलजों की अवधारणा के बारे में है। अनिश्चित समाकलज के लिए, आद्य समाकल देखें।

कलन में, समाकलज एक संकलन का सतत अनुरूप होता है, जिसका उपयोग क्षेत्रफल, आयतन और उनके सामान्यीकरण की गणना करने हेतु किया जाता है। समाकलन, समाकलज की गणना की प्रक्रिया, कलन के दो मूलभूत प्रक्रियाओं में से एक है, दूसरा अवकलन है। गणित और भौतिकी में समस्याओं को हल करने हेतु एक विधि के रूप में समाकलन शुरू हुआ, जैसे वक्र के नीचे क्षेत्रफल खोजना, या वेग से विस्थापन का निर्धारण। वर्तमान समाकलन का प्रयोग विभिन्न प्रकार के वैज्ञानिक क्षेत्रों में किया जाता है।

किसी फलन का निश्चित समाकलज उसके ग्राफ और क्षैतिज अक्ष से घिरे क्षेत्र के चिह्नित क्षेत्रफल द्वारा निरूपित किया जा सकता है।

किसी फलन का निश्चित समाकलज उसके ग्राफ और क्षैतिज अक्ष से घिरे क्षेत्र के चिह्नित क्षेत्रफल द्वारा निरूपित किया जा सकता है। उदाहरणतः ऊपर दिए गए ग्राफ में, ${\displaystyle f(x)}$ का समाकलज पीला (-) क्षेत्र द्वारा घटाया गया नीला (+) क्षेत्र है।

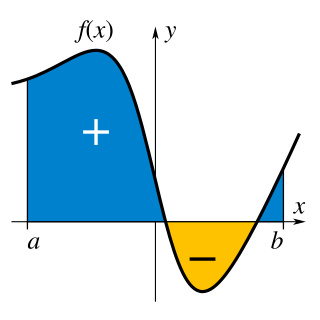
यहाँ बताए गए समाकलज वे हैं जिन्हें निश्चित समाकलज कहा जाता है, जिन्हें संख्या रेखा में दो बिन्दुओं के मध्य दिए गए फलन के ग्राफ द्वारा समतल किए गए क्षेत्र के चिह्नित क्षेत्रफल के रूप में व्याख्या किया जा सकता है। परम्परागत रूप से, समतल के क्षैतिज अक्ष के ऊपर के क्षेत्र धनात्मक होते हैं जबकि नीचे के क्षेत्र ऋणात्मक होते हैं। समाकलन भी एक प्रत्यवकलजों की अवधारणा को सन्दर्भित करता है, एक ऐसा फलन जिसका अवकलज दिया हुआ फलन है। इस स्थिति में, उन्हें अनिश्चित समाकलज कहा जाता है। कलन का मूलभूत प्रमेय अवकलन के साथ निश्चित समाकलजों को सम्बन्धित करता है और किसी फलन के निश्चित समाकलन की गणना करने हेतु एक विधि प्रदान करता है जब इसका प्रत्यवकलज ज्ञात हो।

निरूपण तथा शब्दावली

सामान्यतः, अंतराल ${\displaystyle [a,b]}$ पर वास्तविक चर x के सम्बन्ध में वास्तविक-मान फलन ƒ(x) का x के सापेक्ष समाकलज निम्नोल्लेखित है:

$${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$$

चिह्न ∫ समाकलन का प्रतिनिधित्व करता है। प्रतीक dx, जिसे चर x का अवकलज कहा जाता है, इंगित करता है कि समाकलन का चर x है।

फलन f(x) को समाकल्य कहा जाता है, बिन्द्वों a और b को समाकलन की सीमा कहा जाता है, और समाकलज को अन्तराल [a, b] के ऊपर कहा जाता है, जिसे समाकलन का अन्तराल कहा जाता है। एक फलन को पूर्णांक कहा जाता है यदि इसके प्रभावक्षेत्र पर इसका अभिन्न परिमित है। यदि सीमाएँ निर्दिष्ट हैं, तो समाकलज को निश्चित समाकलज कहा जाता है।

जब सीमाओं का लोप होता है:

$${\displaystyle \int f(x)\,\mathrm {d} x}$$

तब समाकलज को एक अनिश्चित समाकलज कहा जाता है, जो फलनों के एक वर्ग (प्रत्यवकलज) का प्रतिनिधित्व करता है जिसका अवकलज समाकल्य है। कलन का मूलभूत प्रमेय निश्चित समाकलजों के मूल्यांकन को अनिश्चित समाकलजों से सम्बन्धित करती है।

गुणधर्म

रैखिकता

समाकलनीय फलनों का संग्रह रैखिक संयोजनों के तहत बन्द है, और एक रैखिक संयोजन का समाकलज, उसके समाकलजों का रैखिक संयोजन है:

${\displaystyle \int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,}$

समाकलन की विधियाँ

चर परिवर्तन करके समाकलन करना

मुख्य लेख: प्रतिस्थापन द्वारा समाकलन

${\displaystyle \int _{\varphi (a)}^{\varphi (b)}f(x)\,\mathrm {d} x=\int _{a}^{b}f(\varphi (t))\varphi '(t)\,\mathrm {d} t.}$

खण्डशः समाकलन

${\displaystyle \int _{a}^{b}u(x)v'(x)\,\mathrm {d} x=[u(x)v(x)]_{a}^{b}-\int _{a}^{b}u'(x)v(x)\,\mathrm {d} x.}$

आंशिक भिन्न विधि

विभिन्न प्रकार के समाकल

${\displaystyle \int f(x)dx}$ – अनिश्चित समाकल (indefinite intergal)

${\displaystyle \int \limits _{a}^{b}f(x)dx}$ – निश्चित समाकल (Definite integral)

${\displaystyle \int \limits _{-\infty }^{0}f(x)dx}$ – अनंत समाकल improper integral (=infinite integral)

${\displaystyle \int \limits _{E}f(x)dx}$ – लेबेग समाकल (Lebesgue integral)

${\displaystyle \iint \limits _{S}f(x,y,z)\;dS}$ – पृष्ठ समाकल (surface integral)

${\displaystyle \oint \limits _{S}f(x,y)\;dl}$ – किसी बन्द वक्र के सापेक्ष वक्ररेखी समाकल

सन्दर्भ

इन्हें भी देखें

• समाकल सूची
• अवकलन
• निश्‍चित समाकलों की सूची

बाहरी कड़ियाँ

• Riemann Sum by Wolfram Research
• Introduction to definite integrals by Khan Academy
• Integrais por Só Matemática
• Integral Calculus by Duke University Physics Department

आनलाइन पुस्तकें

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Warner, Stefan y Costenoble, Steven R., Matemáticas Finitas y Cálculo Aplicado 7e, libro en linea
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Cuartas, Roberto, Cálculo Integral, Tareas Pkus, libro y curso en linea
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Kowalk, W.P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
• Rudolph, Dennis, Integral-Rechnung / Integrieren Übersicht, Mathematik Übersicht von Projekt Frustfrei-Lernen.de, Online-Lehrbuch
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute
• P.S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) - a cookbook of definite integral techniques