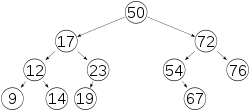
עץ AVL

במדעי המחשב, עץ AVL הוא מבנה נתונים מסוג עץ חיפוש בינארי מאוזן, שבו הפרש גובהם של שני תתי-העצים של הבנים של כל צומת הוא לכל היותר 1. תכונה זו מבטיחה שניתן יהיה לחפש בעץ, להכניס ולהוציא ממנו נתונים בסיבוכיות של ${\displaystyle \ O(\log n)}$ במקרה הגרוע ביותר (כאשר ${\displaystyle \ n}$ הוא מספר הצמתים בעץ).

עץ AVL
דוגמה לעץ AVL
יצירה
הומצא ב:	1962
ממציא:	גאורגי אדלסון-ולסקי ויבגני לנדיס
סיבוכיות מקום וזמן
	ממוצע במקרה הגרוע
זיכרון:	O(n) O(n)
חיפוש:	O(log n) O(log n)
הכנסה:	O(log n) O(log n)
הוצאה:	O(log n) O(log n)

עץ AVL נקרא כך על שם ראשי התיבות של ממציאיו, גאורגי אדלסון-ולסקי (Adelson-Velskii) ויבגני לנדיס (Landis, שהציגו אותו במאמר משנת 1962. היה זה עץ החיפוש הראשון שהבטיח איזון בעלות של ${\displaystyle \ O(\log n)}$.

דרך פעולת העץ

כל צומת בעץ שומר, פרט למידע הסטנדרטי של עץ חיפוש, גם מאפיין נוסף הנקרא "גורם האיזון" (Balance factor). מאפיין זה הוא ההפרש בין גובהו של תת-העץ השמאלי של הצומת וגובה תת-העץ הימני של הצומת. עץ AVL מאופיין בכך שגורם האיזון בכל צומת הוא תמיד 1, 0 או 1-, ופעולות הוספה והסרה שומרות על תכונה זו. תכונה זו מבטיחה כי העץ יהיה מאוזן בקירוב - ניתן להראות^[1] כי אם בעץ AVL יש ${\displaystyle n}$ איברים אז עומקו קטן מ- ${\displaystyle 1.44\cdot \log _{2}(n+2)-0.328}$ (העומק המינימלי בעץ חיפוש מאוזן לגמרי הוא ${\displaystyle \lceil \log _{2}(n+1)\rceil }$, עץ AVL יכול להיות בעומק גדול יותר).

פעולת חיפוש

החיפוש בעץ AVL הוא רקורסיבי וזהה לחיפוש בעץ חיפוש בינארי. הרקורסיה מתחילה משורש העץ. בודקים עבור הצומת הנוכחי:

1. אם מפתח הצומת מתאים למפתח המבוקש - החיפוש הסתיים בהצלחה.
2. אם מפתח הצומת גדול מהמפתח המבוקש - מבצעים חיפוש שמתחיל בצומת שהוא הבן השמאלי של הצומת הנוכחי, ומחזירים את התוצאה.
3. אם מפתח הצומת קטן מהמפתח המבוקש - מבצעים חיפוש בצומת שהוא הבן הימני של הצומת הנוכחי, ומחזירים את התוצאה.
4. אם לא התקיים אחד מהסעיפים הקודמים - הנתון המבוקש לא נמצא בעץ.

כיוון שעץ AVL הוא מאוזן בקירוב (כמפורט לעיל), פעולת החיפוש תתבצע בסיבוכיות זמן ${\displaystyle \ O(\log n)}$ כי פעולת החיפוש מתחילה משורש העץ ומשם יכולה להגיע, במקרה הגרוע, עד לעלה העמוק ביותר.

פעולת החיפוש לא משנה את המבנה של העץ ולכן העץ נשמר כעץ חיפוש בינארי ומאוזן.

גלגול

תיאור סכמטי של איזון צומת בעץ בעזרת גלגול. העיגולים הממוספרים מייצגים את הצמתים שמשתתפים בתהליך האיזון. המשולשים מייצגים תתי-עצים שהם עצמם עצי AVL מאוזנים. מספר כחול ליד צומת מציין גורמי איזון אפשריים (אלה שבסוגריים מתקיימים רק במקרה של מחיקה).

כדי לבצע הכנסה ומחיקה מעץ AVL, משתמשים תחילה בפעולה הרצויה כאילו מדובר בעץ חיפוש בינארי פשוט.

הבעיה שנוצרת היא, שבעקבות ההכנסה או ההוצאה מהעץ, ייתכן שגורם האיזון יעלה ל-2 או ירד ל-2-. כדי לפתור את הבעיה, משתמשים בטכניקה הנקראת גלגול, בעזרתה משנים את מבנה העץ כדי לתקן איזון של תת-עץ המתחיל בצומת שבו יש חריגה בגורם האיזון, וזאת מבלי להפר את הסדר של העץ (המאפשר חיפוש בינארי עליו).

ישנם ארבעה סוגים של גלגולים: RR, LL, RL ו-LR, כאשר על ידי ארבעתם ניתן לטפל בכל צומת שגורם האיזון שלו הופר ושווה ל-2 או 2-, בהנחה שהוא תקין בשני עצי הבנים שלו. הבחירה באיזה גלגול להשתמש נעשית על פי הכללים הבאים:

• LL - גורם האיזון בצומת הופר ל-2 וגורם האיזון בבן השמאלי הוא 0 או 1.
• LR - גורם האיזון בצומת הופר ל-2 וגורם האיזון בבן השמאלי הוא 1-.
• RR - גורם האיזון בצומת הופר ל-2- וגורם האיזון בבן הימני הוא 0 או 1-.
• RL - גורם האיזון בצומת הופר ל-2- וגורם האיזון בבן הימני הוא 1.

הגלגולים נעשים בדרך שמתוארת בציור שמופיע בצד. ניתן לממש את כל אחד מארבעת הגלגולים בעזרת שתי פעולות בסיסיות (R ו-L), כאשר הגלגול כולל פעולת R/L אחת שמבוצעת על אחד מהבנים של הצומת, ופעולת R/L שנייה על הצומת עצמו. כל סוגי הגלגולים הם בזמן קבוע של ${\displaystyle O(1)}$

פעולת הכנסה

כדי להכניס צומת חדש לעץ, מתחילים במציאת המקום המתאים להכנסה באותה הדרך שבה מכניסים לעץ חיפוש בינארי. מתחילים משורש העץ ובודקים באופן רקורסיבי:

1. אם מפתח הצומת גדול מהמפתח שרוצים להכניס לעץ. אם קיים בן שמאלי לצומת - מבצעים את הבדיקה עבור תת-העץ המתחיל בבן זה. אחרת, הצומת החדש יהיה הבן השמאלי של הצומת.
2. אם מפתח הצומת קטן מהמפתח שרוצים להכניס לעץ. אם קיים בן ימני לצומת - מבצעים את הבדיקה עבור תת-העץ המתחיל בבן זה. אחרת, הצומת החדש יהיה הבן הימני של הצומת.

לאחר שהצומת הוכנס לעץ, צריך לבדוק את המסלול מהצומת החדש כלפי מעלה עד לשורש, ואם קיים צומת שגורם האיזון שלו הופר - לבצע גלגול עבור צומת זה. פעולת הגלגול מחזירה את הגובה של תת-העץ שעל שורשו היא פועלת לגובה שהיה לפני ההוספה, ולכן העץ נשאר מאוזן לאחר גלגול זה.

פעולת ההכנסה מבוצעת בסיבוכיות זמן ${\displaystyle O(\log n)}$ כי פעולת ההכנסה המקורית מבוצעת בסיבוכיות זמן ${\displaystyle O(\log n)}$, יש לכל היותר ${\displaystyle \log n}$ צמתים שצריך לעדכן את גורם האיזון שלהם, ולא יותר מגלגול אחד^[2], שמשנה רק מספר קבוע של צמתים.

פעולת מחיקה

כאשר רוצים להוציא צומת מתוך עץ AVL, צריך לבצע שלושה תהליכים עיקריים - מציאת הצומת שצריך להוציא, הוצאת הצומת תוך שמירה על תכונת עץ החיפוש ואיזון העץ לאחר ההוצאה.

מציאת הצומת

מציאת הצומת נעשית באותה הדרך שנעשית פעולת החיפוש וניתן לדלג על מציאת הצומת במקרים שבהם נתון מראש הצומת שדורש מחיקה.

הוצאת הצומת

בהינתן צומת ${\textstyle v}$ שרוצים להוציא מתוך העץ אך להשאיר את העץ כעץ AVL, מבצעים את הפעולות הבאות:

• אם אין בנים ל${\textstyle v}$ אז מוחקים אותו מהעץ.
• אם ל${\textstyle v}$ יש בן אחד, מוחקים את ${\textstyle v}$ והאבא של v מצביע לבן שלו.
• אם ל${\textstyle v}$ יש שני בנים, אז צריך למצוא את הצומת העוקב ל-${\textstyle v}$ ולהחליף ביניהם. העוקב של ${\textstyle v}$ הוא הצומת השמאלי ביותר שאליו אפשר להגיע מהבן הימני של ${\textstyle v}$ (${\textstyle v_{rlll..}}$). לאחר ההחלפה מוחקים את ${\textstyle v}$ לפי אחת מהפעולות הקודמות.

איזון העץ לאחר ההוצאה

כיוון שהוצאת הצומת יכולה לגרום לכך שהעץ כבר אינו מאוזן, עוברים על המסלול מהצומת שנמחק עד לשורש העץ וכל פעם שקיים צומת שגורם האיזון שלו הופר, מבצעים את הגלגול ששייך לאותו הצומת.

פעולת ההוצאה, כמו פעולת ההכנסה, מבוצעת בסיבוכיות זמן ${\displaystyle O(\log n)}$.

סריקת העץ

לפעמים קיים צורך לעבור על כל הנתונים שנמצאים בעץ ולבצע פעולה, למשל עדכון בכל הנתונים, שמירה למבנה ליניארי (כמו קובץ) או חיפוש נתון שלא ידוע מה המפתח שלו. קיימות מספר דרכים לעבור על כל הנתונים, כאשר הכלל המנחה שלהם הוא שעבור כל צומת בעץ החל מהשורש צריך לבצע פעולה בנתון שלו ולסרוק גם את הצמתים הבנים. כדי לקבל את הנתונים לפי סדר יש לעבור על עץ החל מהשורש, בצורה רקורסיבית בשיטת סדר תּוֹכִי (in-order traversal). עבור הצומת הנוכחי המעבר מתבצע באופן הבא:

1. בצע את הסריקה עבור הבן השמאלי של הצומת.
2. בצע את הפעולה הנדרשת.
3. בצע את הסריקה עבור הבן הימני של הצומת.

סריקה כזו של העץ תעבור על כל הצמתים בעץ לפי סדר מהקטן לגדול, בזמן ריצה ${\displaystyle \Theta (n)}$.

בנוסף קיימות 2 סריקות נוספות: תחילית (pre-order) וסופית (post-order).

קישורים חיצוניים

מדיה וקבצים בנושא עץ AVL בוויקישיתוף

• איך לאזן עץ AVL, מדריך בצעדים.

הערות שוליים

1. Knuth, Donald E. (2000). The art of computer programming, Volume 3: Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Addison-Wesley. p. 460. ISBN 0-201-89685-0.
2. מאחר שלאחר גלגול גורם האיזון של כל מה שמעליו חוזר להיות כמו לפני ההכנסה