סריגי בראבה

סריגי בְּרָאבֶה הם מחלקות של סריגים, הממוינות לפי מידת הסימטריה של הסריג. למיון זה חשיבות רבה במיון של גבישים על-פי המבנה המרחבי שלהם, ובתחומים אחרים בפיזיקה של מצב מוצק. סריגי בראבה קרויים על שמו של הפיזיקאי הצרפתי אוגוסט בראבה (Auguste Bravais) שגילה אותם ב-1848.

הקדמה

ערך מורחב – סריג (גאומטריה)

סריג הוא אוסף אינסופי של נקודות, הנוצר באמצעות אוסף בדיד של פעולות הזזה, כך שמתקיימת התכונה:

הסריג נראה אותו דבר, מכל נקודה בסריג בה מביטים עליו.

הגדרה נוספת, ושקולה לקודמת, מראה כיצד ליצור בפועל סריג ${\displaystyle n}$-ממדי: נבחר ${\displaystyle n}$ וקטורים בלתי תלויים ליניארית, ${\displaystyle {\vec {e_{1}}},{\vec {e_{2}}},\cdots ,{\vec {e_{n}}}}$. (קבוצה זו נקראת "בסיס פרימיטיבי לסריג", או לפעמים "בסיס ראשוני"). הקבוצה

${\displaystyle L=\left\{{\vec {R}}=\lambda _{1}{\vec {e_{1}}}+\cdots +\lambda _{n}{\vec {e_{n}}}\ |\ \lambda _{1},\cdots ,\lambda _{n}\in \mathbb {Z} \right\}}$

היא סריג. במילים אחרות, הסריג נפרש על ידי כל הצירופים הליניאריים במקדמים שלמים של וקטורי הבסיס הפרימיטיבי. צירופים אלו (כלומר, איברי ${\displaystyle L}$), נקראים וקטורי סריג.

${\displaystyle n}$ הווקטורים בבסיס הפרימיטיבי מגדירים מקבילון, המכונה תא יחידה, שאיתו אפשר לרצף באופן מחזורי ושלם את המרחב.

סימטריה

כל הסריגים מקיימים מספר תכונות:

• סימטריה ביחס להזזה בווקטור סריג: אם נזיז את כל נקודות הסריג בווקטור סריג, נקבל בחזרה את אותו סריג.

באופן מתמטי: אם ${\displaystyle v\in L}$, אז ${\displaystyle L+v=L}$.

• סימטריה לסיבוב ב-180° (או: ${\displaystyle \pi }$ רדיאנים): אם נבחר נקודה במרחב, ונסובב סביבה את הסריג בחצי סיבוב, נקבל חזרה את אותו סריג.
• סימטריה ביחס לשיקוף מלא: אם נחליף כל וקטור סריג בשיקוף שלו – כלומר ${\displaystyle v\to -v}$ – נקבל אותו סריג.

הסימטריות הנוספות שעשויות להיות לסריגים מחלקות אותם לקבוצות (מחלקות שקילות), תוך התעלמות מהגדלים הפיזיים של הסריג (פרמטרי הסריג) – קבוצות אלו הן סריגי בראבה.

סריגי בראבה דו־ממדיים

ב-0 ממדים ובממד אחד, יש רק סריג בראבה אחד.

בשני ממדים, ניתן להבחין בין חמישה סריגי בראבה, לפי מידת הסימטריה שיש לכל אחד מהם, בנוסף לסימטריות שיש לכל הסריגים:

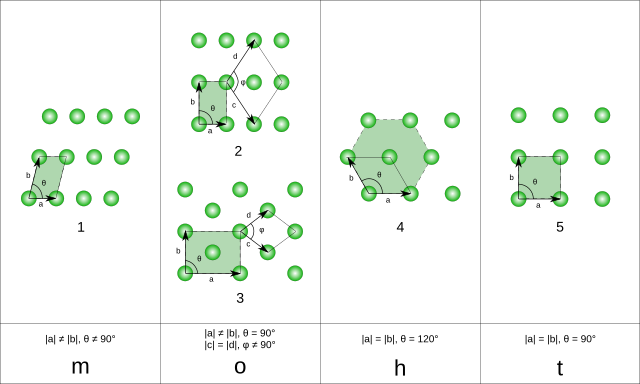
1. לסריג כללי (oblique) אין סימטריות נוספות.
2. לסריג מלבני (rectangular) יש סימטריה לשיקוף ביחס לשני מישורים (קווים במרחב הדו-ממדי).
3. לסריג מלבני ממורכז (centered rectangular)^[1] יש אותן סימטריות סיבוב ושיקוף של סריג מלבני, אבל סימטריות הזזה שונות.
4. לסריג משושה (hexagonal) יש, בנוסף לסימטריה של סריג מלבני ממורכז, סימטריה לסיבוב בכפולות של 60° (או: ${\displaystyle {\tfrac {\pi }{3}}}$ רדיאנים).
5. לסריג ריבועי (square) יש, בנוסף לסימטריה של סריג מלבני, סימטריה לסיבוב ב-90° (${\displaystyle {\tfrac {\pi }{2}}}$ רדיאנים), ולשיקוף ביחס ל"אלכסון" של הריבוע.

סריגי בראבה תלת־ממדיים

ניתן להראות שיש בסך הכול 14 סריגי בראבה תלת-ממדיים אפשריים. הללו מתבססים על 7 מקבילונים (7 מערכות גבישיות), עם 6 אפשרויות להוספת נקודות סריג נוספות במרכזי הפאות או הגוף.

שש האפשרויות להוספת נקודות ("מרכוז"; "centering") הן:

• P – פשוט (Primitive centering) – ללא הוספת נקודות.
• I^[2] – ממורכז גוף (Body centered; BC) – מוסיפים נקודת סריג אחת במרכז כל תא.
• F – ממורכז פאה (Face centered; FC) - מוסיפים נקודת סריג אחת בכל פאה של תא היחידה.
• C – מרכז חד-פאה (Base centered) - בוחרים זוג אחד מפאותיו של תא היחידה ומוסיפים להם נקודת סריג אחת לכל פאה (הוספת נקודת סריג בפאה השנייה מתחייבת מסימטריה ביחס להזזה בווקטור סריג). אלו 3 אפשרויות, שכן יש 3 אפשרויות לבחור את זוג הפאות שיתווספו להן נקודות סריג.

לכאורה, מהאמור לעיל אמורים להתקבל 42 מבני סריג אפשריים במרחב תלת-ממדי (7 מערכות גבישיות כפול 6 אפשרויות להוספת נקודות). אולם, כאשר מנסים לבנות אותם מגלים שחלק גדול מהמבנים האפשריים זהים למבנים אחרים. עם הפחתת הכפילויות מגלים שיש בסך הכול 14 סריגים תלת-ממדיים השונים זה מזה, והם מסוכמים בטבלה להלן:

מערכות גבישים	סריג:
טריקליני (Triclinic)
מונוקליני (Monoclinic)	פשוט	ממורכז בסיס
אורתורומבי (Orthorhombic)	פשוט	ממורכז בסיס	ממורכז גוף	ממורכז פאה
משושה (Hexagonal)
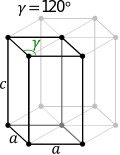טריגונלי (או: רומבוהדרלי) (Trigonal; Rhombohedral)
טטרגונלי (Tetragonal)	פשוט	ממורכז גוף
קובייתי (Cubic)	פשוט	ממורכז גוף	ממורכז פאה

חבורות הסימטריות הנקודתיות של כל אחד מהסריגים האלו תלויות, במערכת הגבישית. בנוסף, כתלות במרכוז, יש לכל אחד מהסריגים חבורות סימטריות מרחביות.

דוגמה: סריג קובי פשוט

ערך מורחב – המערכת הגבישית הקובייתית

סריג קובי פשוט

סריג קובי פשוט הוא סריג שכל צלעותיו זהות באורכן וניצבות זו לזו. ניתן לחשוב עליו כעל ריצוף כל המרחב התלת-ממדי בקוביות (באופן דומה לריצוף דף דו-ממדי במשבצות ריבועיות).

כדי לתאר סריג ספציפי לא מספיק לתאר את סריג בראבה שלו (קובי, בדוגמה זו), אלא גם פרמטרים נוספים (במקרה זה, אורך הצלע), הנקראים "פרמטרי סריג". אם ידוע שאורך הצלע הוא a, אז התיאור המתמטי שלו יהיה קבוצת הווקטורים שנפרשת (במקדמים שלמים) על ידי הבסיס הפרימיטיבי הבא:

${\displaystyle \ {\vec {e_{1}}}=a{\hat {x}}\$ ;\ {\vec {e_{2}}}=a{\hat {y}}\ ;{\vec {e_{3}}}=a{\hat {z}}}

במקרה זה, ניתן לבחור את תא היחידה הפרימיטיבי כקובייה שנפחה a³.

לסריג כזה יש שלושה צירי סימטריה לסיבוב ב-90°, ארבעה צירי סימטריה לסיבוב ב-120°, שישה צירי סימטריה לסיבוב ב-180°, תשעה מישורי סימטריה לשיקוף ומרכז סימטריה. לכן, משויכות לו 5 חבורות סימטריה נקודתיות^[3], ו-15 חבורות סימטריה מרחביות.

ראו גם

• פרמטר סריג
• סריג הופכי
• תא ויגנר-זייץ
• גביש
• קריסטלוגרפיה

קישורים חיצוניים

מדיה וקבצים בנושא סריגי בראבה בוויקישיתוף

• science/crystal-lattice סריגי בראבה, באתר אנציקלופדיה בריטניקה (באנגלית)
• סריגי בראבה, באתר MathWorld (באנגלית)

הערות שוליים

1. בנוסף על התנאי המפורש באיור, סריג זה מקיים את התנאי ${\displaystyle 2\mathbf {a} _{2}-\mathbf {a} _{1}\perp \mathbf {a} _{1}}$. תנאי זה גורם לכך שהסריג יהיה מלבני, אך גם מכריח ${\displaystyle \varphi \neq 90^{\circ }}$.
2. לפעמים מסומן ב-B.
3. המשויכות גם לסריג הקובי ממורכז הגוף (BCC) וגם לסריג הקובי ממורכז הפאה (FCC): הטטרטואידלית, הדיפלואידלית, הגירודיאלית, ההקסטטרהדרלית וההקסאוקטהדרלית.