Un favo,[1] tamén chamado entena,[2] panal,[3] trevo[4] ou zarapata[5] é unha estrutura construída con cera polas abellas melíferas, como resultado das celas hexagonais que comparten paredes en común.
Construción e características
Esta capacidade débese a que as obreiras contan con glándulas cereiras que producen este elemento natural. O panal é empregado para depositar os seus alimentos: pole e mel. Tamén a cela é utilizada como habitáculo para a cría de obreiras e abellóns. O tamaño da cela varía segundo a necesidade da abella, sendo de aproximadamente 6 milímetros para obreiras e 8 milímetros para abellóns no caso de Apis mellifera.
As diferentes especies do xénero Apis constrúen diferentes tamaños de celas, adecuados ás súas respectivas castes, o que é moi útil para distinguir as especies e as razas do xénero.
Nas abellas de niño pechado, Apis cerana e Apis mellifera, os panais son construídos en forma transversal ao orificio de entrada da colmea. Deste xeito, os panais anteriores próximos á entrada (piqueira) fan de barreira natural á entrada de aire frío.
A unha distancia de dez celas de panal construído pola abella oriental (Apis cerana) en Filipinas ten unha media de 4,1 centímetros, e no sur da India, a distancia é 4,3 a 4,4 centímetros. As razas africanas da abella occidental (Apis mellifera) constrúen panais con medidas de 4,7 a 4,9 centímetros por cada 10 celas, mentres a distancia dos panais construídos polas razas europeas comúns é 5,2 a 5,6 centímetros cada 10 celas.
Nos panais de cera da colmea rústica (ocos de árbores) ou nas colmeas que non teñen cadros móbiles a construción non é sempre paralela, xa que as abellas constrúen os panais en diferentes radios.
Espazo abella
O espazo abella, que é o lugar polo cal as abellas transitan entre os cadros e na colmea, é o espazo natural que a abella separa un panal do adxacente. Este espazo foi descuberto por Lorenzo Langstroth para a Apis mellifera, sendo diferente do da Apis cerana, aínda que moi parecido. Non respectar este espazo fai que a abella encha o mesmo con própole. Nunca debe ser menor a 5 milímetros, nin maior a 9 milímetros porque construirá panal de cera. Hai autores que definen o espazo abella como 7,5 mm.
Panais de cera en apicultura racional
Na apicultura racional, o panal de cera é construído dentro dun marco móbil de madeira, para que a abella manteña unha liña de construción determinada con antelación polos apicultores. Para iso se desenvolveu unha lámina de cera estampada que é adherida a arames que cruzan o marco en forma horizontal ou vertical. Estes panais teñen dimensións preestablecidas polos tamaños dos cadros móbiles, o mesmo que a lámina de cera estampada. Sobre esta base as abellas constrúen as súas celas cunha leve inclinación superior dende o fondo á boca, co propósito de que non se derramo o mel que gardan no interior.
Na apicultura racional a disposición dos panais que se emprega frecuentemente é lonxitudinal con respecto á entrada da colmea (piqueira), o que permite unha mellor aireación dos mesmos e facilita o secado do néctar, evitando o traballo de ventilación que teñen que desenvolver as obreiras. A diferenza dos panais naturais que son construídos transversalmente ao orificio de entrada da colmea, denominado exposición en quente, a colmea racional utiliza o método chamado exposición en frío para os seus panais lonxitudinais con respecto á entrada da mesma. Hai colmeas construídas para ser empregadas con panais de exposición en quente, pero son as menos e xeralmente utilízanse en climas fríos ou tépedos fríos.
Ángulo das celas dos panais
É interesante ver a xeometría dunha cela de panal, e a forma en que estas encastran co panal oposto do marco móbil.
Xeometría tridimensional dunha cela de panal.
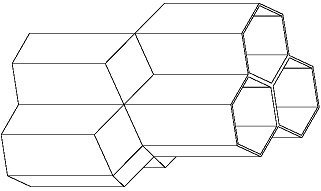Celas de panal de lados opostos.
En 1700 fixéronse cálculos referentes á medida dos ángulos dos rombos nos fondos piramidais das celas do panal. O enxeñeiro italiano, Maraldi, astrónomo, estudou as celas da abella e mediu o longo das mesmas atopando que son aproximadamente iguais unhas das outras. Entón mediu os ángulos das celas dun panal, calculando que era de 109º 28'.
Reaumur sospeitou que as abellas economizaban cera, consultando ó matemático Koenig, para resolver o problema de celas da abella. Koenig calculou o ángulo máis grande dos rombos obtendo 109º 26'. Investigacións posteriores demostraron que 109º 28' era a resposta correcta.
Outros científicos que viron nas abellas a posibilidade de atopar o ángulo perfecto obtiveron o mesmo resultado que Koenig. Anos máis tarde, a investigación dun accidente marítimo demostrou que o capitán dirixira mal o curso do seu barco, debido ao cálculo das táboas de logaritmo existentes que eran defectuosos. As táboas foron corrixidas para previr un erro adicional. Entón descubriuse que estas eran as mesmas táboas logarítmicas coas cales Koenig fixera os seus cálculos. O problema do ángulo das celas foi solucionado outra vez, coas táboas corrixidas, e os ángulos obtidos foron os que as abellas utilizaran sempre: 109º 28'.
Galería de imaxes
- Vexa o artigo principal en Galería de imaxes de apicultura en Galicia
Notas
Véxase tamén
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
