Extremos dunha función

En matemáticas, os máximos e mínimos dunha función, coñecidos colectivamente como extremos dunha función, son os valores meirandes (máximos) ou máis pequenos (mínimos) que toma unha función nun punto situado xa sexa dentro dunha rexión en particular da curva (extremo local) ou no dominio da función na súa totalidade (extremo global ou absoluto).^[1][2][3] De maneira máis xeral, os máximos e mínimos dun conxunto (como se define en teoría de conxuntos) son os elementos maior e menor no conxunto, cando existen. O localizar valores extremos é o obxectivo básico da optimización matemática.

Extremos dunha función.

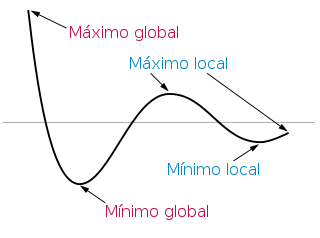
Extremos relativos ou locais

Sexa ${\displaystyle f(x):A\subset \mathbb {R} \longrightarrow \mathbb {R} }$, sexa ${\displaystyle x_{0}\in A}$ e sexa ${\displaystyle P\,(x_{0},f(x_{0}))}$ un punto pertencente á función.

Dise que ${\displaystyle p}$ é un máximo local de ${\displaystyle f}$ se existe unha veciñanza reducida de centro ${\displaystyle x_{0}}$, en símbolos ${\displaystyle {E'(x_{0})}}$, onde para todo elemento ${\displaystyle x}$ de ${\displaystyle {E'(x_{0})}}$ se cumpre que ${\displaystyle f(x)\leq f(x_{0})}$. Para que esta propiedade posúa sentido estrito debe cumprirse ${\displaystyle f(x)<f(x_{0})}$.

Analogamente, dise que o punto ${\displaystyle p}$ é un mínimo local de ${\displaystyle f}$ se existe unha veciñanza^[4] reducida de centro ${\displaystyle x_{0}}$, en símbolos ${\displaystyle {E'(x_{0})}}$, onde para todo elemento ${\displaystyle x}$ de ${\displaystyle {E'(x_{0})}}$ se cumpre que ${\displaystyle f(x)\geq f(x_{0})}$.

Extremos absolutos

Sexa ${\displaystyle f(x):A\subset \mathbb {R} \longmapsto \mathbb {R} }$, sexa ${\displaystyle x_{0}\in A}$ e sexa ${\displaystyle P\,(x_{0},f(x_{0}))}$ un punto pertencente á función.

Dise que ${\displaystyle P}$ é un máximo absoluto de ${\displaystyle f}$ se, para todo ${\displaystyle x}$ distinto de ${\displaystyle x_{0}}$ pertencente ao subconxunto ${\displaystyle A}$, a súa imaxe é menor ou igual ca a de ${\displaystyle x_{0}}$. Isto é:

${\displaystyle P\,(x_{0},f(x_{0}))}$ máximo absoluto de ${\displaystyle f\iff \forall x\neq x_{0},x\in A,f(x_{0})\geq f(x)}$.

Analogamente, ${\displaystyle P}$ é un mínimo absoluto de ${\displaystyle f}$ se, para todo ${\displaystyle x}$ distinto de ${\displaystyle x_{0}}$ pertencente ao subconxunto ${\displaystyle A}$, a súa imaxe é maior ou igual ca a de ${\displaystyle x_{0}}$. Isto é:

${\displaystyle P\,(x_{0},f(x_{0}))}$ mínimo absoluto de ${\displaystyle f\iff \forall x\neq x_{0},x\in A,f(x_{0})\leq f(x)}$.

Cálculo de extremos locais

Dada unha función suficientemente derivábel ${\displaystyle f(x):A\subset \mathbb {R} \longrightarrow \mathbb {R} }$, definida nun intervalo aberto de ${\displaystyle \mathbb {R} }$, o procedemento para achar os extremos desta función é moi sinxelo:

1. Áchase a primeira derivada de ${\displaystyle f\rightarrow f'\,(x)}$
2. Áchase a segunda derivada de ${\displaystyle f\rightarrow f''\,(x)}$
3. Iguálase a primeira derivada a 0: ${\displaystyle f\,'(x)=0}$
4. Despéxase a variábel independente e obtéñense todos os valores posíbeis da mesma: ${\displaystyle x={\big \{}x_{1},x_{2},...,x_{n}/f'(x_{i})=0\quad \forall i=1,2,...,n{\big \}}}$.
5. Áchase a imaxe de cada ${\displaystyle x_{i}\,}$ substituíndo a variábel independente na función.
6. Agora, na segunda derivada, substitúese cada ${\displaystyle x_{i}\,}$:
   1. Se ${\displaystyle f''\,(x_{i})<0}$, tense un máximo no punto ${\displaystyle M\,(x_{i},f(x_{i}))}$.
   2. Se ${\displaystyle f''\,(x_{i})>0}$, tense un mínimo no punto ${\displaystyle m\,(x_{i},f(x_{i}))}$.
   3. Se ${\displaystyle f''\,(x_{i})=0}$, debemos substituír ${\displaystyle x_{i}\,}$ nas sucesivas derivadas até que sexa distinto de cero. Cando se ache a derivada para a que ${\displaystyle x_{i}\,}$ non sexa nulo, hai que ver que derivada é:
      1. Se a derivada é par, trátase dun extremo local; un máximo se ${\displaystyle f^{n}\,(x_{i})<0}$ e un mínimo se ${\displaystyle f^{n}\,(x_{i})>0}$
      2. Se a derivada non é par, trátase dun punto de inflexión, pero non dun extremo.

Exemplo

Sexa ${\displaystyle f(x)=x^{3}-12x^{2}+45x-30\,}$. Achar os seus extremos locais e os seus puntos de inflexión.

Dada a función ${\displaystyle f(x)=x^{3}-12x^{2}+45x-30\,}$, tense que:

${\displaystyle f'\,(x)=3x^{2}-24x+45}$

${\displaystyle f''\,(x)=6x-24}$

${\displaystyle f'''\,(x)=6}$

• Extremos:

${\displaystyle f'\,(x)=3x^{2}-24x+45=0\iff x\in {\big \{}3,5{\big \}}}$

${\displaystyle f''\,(3)=6\cdot 3-24=-6<0\Rightarrow }$ existe un máximo en ${\displaystyle M\,(3,f(3))\rightarrow M\,(3,24)}$.

${\displaystyle f''(5)=6\cdot 5-24=6>0\Rightarrow }$ existe un mínimo en ${\displaystyle m\,(5,f(5))\rightarrow m\,(5,20)}$.

• Puntos de inflexión:

${\displaystyle f''(x)=6x-24=0\iff x=4}$.

${\displaystyle f'''(4)=6\neq 0\Rightarrow }$ existe un punto de inflexión en ${\displaystyle P\,(4,f(4))\rightarrow P\,(4,22)}$.

Notas

1. Stewart, James (2008): Calculus: Early Transcendentals. Brooks/Cole. 6ª ed. ISBN 0-495-01166-5
2. Larson, Ron & Edwards, Bruce H. (2009): Calculus. Brooks/Cole. 9ª ed. ISBN 0-547-16702-4
3. Thomas, George B., Weir, Maurice D. & Joel (2010): Thomas' Calculus: Early Transcendentals. Addison-Wesley. 12ª ed. ISBN 0-321-58876-2
4. Masa Vázquez, Xosé M.; Fortes López, Belén (1995). Servicio de Normalización Lingüística da Universidade de Santiago de Compostela, ed. Vocabulario de Matemáticas. Santiago de Compostela. ISBN 84-8121-369-1.