Loading AI tools
De Wikipédia, l'encyclopédie libre
La trilatération est une méthode mathématique permettant de déterminer la position relative d'un point en utilisant la géométrie des triangles tout comme la triangulation. Mais contrairement à cette dernière, qui utilise les angles et les distances pour positionner un point, la trilatération utilise les distances entre trois points de référence.
Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Dans le cas d'utilisation de plus de 3 points, on parle de multilatération[1].
Une onde électromagnétique émise par une antenne non-directionnelle perd en intensité proportionnellement au carré de la distance du point d'émission, l'énergie du signal se répartissant sur une sphère dont le rayon augmente à la vitesse de propagation de l'onde.
Si trois points de référence émettent un signal d'intensité d'émission connue par un récepteur, il est possible de connaitre la distance entre chacun de ces points et le récepteur. Il apparait alors le point récepteur qui est l'intersection de 3 sphères.
Il est important de noter que la méthode décrite ci-dessus marche dans le cas où le signale se propage dans un système connu. Dans le cas le plus simple, on considère que le signal se propage dans un système isotrope et homogène.
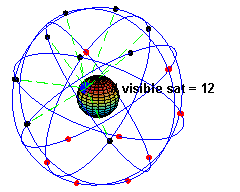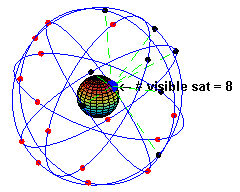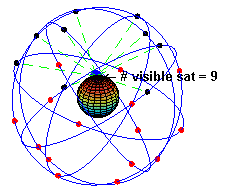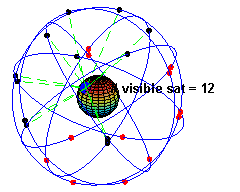
Un cas d'application est le Système de positionnement par satellites. Cependant, trois satellites ne sont pas suffisants, un quatrième est au moins requis pour le recalage des horloges, cela permet de calculer des déplacements. Dans la réalité, le récepteur utilise le maximum de satellites disponible (dont le récepteur reçoit un signal le moins perturbé possible) afin de calculer de la manière la plus optimale sa position en évaluant les erreurs[1].
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
