Réseau de Bravais

En cristallographie, un réseau de Bravais est une distribution régulière de points – appelés nœuds – dans l’espace qui représente la périodicité de la distribution atomique d’un cristal. Les nœuds peuvent être imaginés comme les sommets des mailles, c'est-à-dire des portions de l'espace dans lesquelles la structure cristalline peut être divisée. La structure est alors reconstruite par simple translation de la maille. La donnée d'un réseau de Bravais n'est pas suffisante pour caractériser un cristal : d'une part le cristal est constitué d'atomes et non de nœuds, et d'autre part la maille peut contenir plusieurs atomes, ce qui fait que certaines symétries du réseau ne sont pas forcément des symétries de la structure cristalline : c'est le cas des cristaux mérièdres. Lorsque la symétrie complète du réseau de Bravais est réalisée aussi dans la structure cristalline on parle de cristaux holoèdres.

Formellement, un réseau de Bravais en dimension n est défini comme l'ensemble des vecteurs {m₁a₁ + m₂a₂ + ... + m_na_n}, où m₁, ..., m_n appartiennent à Z et où les vecteurs de base du réseau a₁, ..., a_n sont n vecteurs linéairement indépendants. Les paramètres du réseau sont constitués des longueurs a₁, ..., a_n et des angles entre les vecteurs de base du réseau.

La périodicité engendre un groupe de symétrie constitué des opérations de translation et de rotation laissant le réseau de Bravais invariant. Si le nombre de réseaux est infini, puisqu'à chaque valeur des paramètres il correspond un réseau différent, le nombre de « types » de réseaux (appelés des « modes » de réseau) est fini, le type d'un réseau étant défini par son groupe de symétrie. On dénombre ainsi 5 types de réseau de Bravais dans l'espace bidimensionnel et 14 types dans l'espace tridimensionnel.

Lorsqu'il existe dans un cristal une invariance par rotation, on dit qu'il existe un axe de symétrie d'ordre 2, 3, 4 ou 6, selon que la rotation en question correspond respectivement à un angle de ± 180°, ± 120°, ± 90° ou ± 60°. L'étude des réseaux de Bravais à l'aide de la théorie des groupes a montré que dans les espaces bidimensionnel et tridimensionnel il n'existe pas de cristal ayant un axe de symétrie d'ordre 5. Ceci n'est plus vrai si la distribution atomique n'est pas périodique, comme c'est le cas dans un quasi-cristal : la distribution atomique observée peut alors être interprétée mathématiquement comme la projection sur l'espace tridimensionnel d'une coupe irrationnelle d'une structure périodique de dimension supérieure (4, 5 ou 6).

Un réseau étant infini, il est décrit par une maille, qui représente l’unité par répétition infinie de laquelle le réseau est obtenu. Le choix de la maille n’est pas unique, chaque réseau pouvant en principe être décrit par une infinité de mailles différentes ; ainsi, l'expression paramètres du réseau indique en réalité les paramètres de maille. Deux types de mailles sont utilisés le plus souvent : la maille primitive (ou élémentaire) et la maille conventionnelle : dans chaque famille cristalline il existe un réseau dont la maille conventionnelle est primitive. Les cristaux dont les mailles conventionnelles sont transformées l'une en l'autre en ajoutant ou supprimant des nœuds soit au centre des faces, soit à l'intérieur du volume de la maille, appartiennent à la même famille cristalline.

Mathématiques

Dans un réseau, il existe une famille (illustrée en rouge sur la figure) telle que tout point s'exprime comme combinaison linéaire de manière unique, des points de la famille.

Un réseau de Bravais correspond à une question d'ordre mathématique. Il est associé à l'étude d'un quasi espace vectoriel, la différence entre un espace vectoriel et un réseau étant que dans ce dernier les scalaires sont des entiers et non plus des nombres inversibles (à l'exception de 0) comme les réels ou les complexes. Pour bénéficier d'une géométrie aisément préhensible, le réseau est plongé dans un espace vectoriel euclidien de dimension minimale. Cet espace est, par définition d'un réseau, de dimension finie. Enfin, le réseau peut également être vu comme un espace affine.

Deux domaines fondamentaux, ou mailles primitives, ont même volume.

Une des premières propriétés est le fait que, à l'image de la structure d'espace vectoriel, il existe une base et, si une telle base n'est pas unique, son volume l'est. Le domaine fondamental d'une base est formé par l'ensemble des vecteurs dont les coordonnées dans la base sont dans l'intervalle [0,1[, ce que le cristallographe appelle la maille primitive. La figure de droite illustre deux domaines fondamentaux, en vert et en rouge, nécessairement de même volume.

Plusieurs groupes apparaissent naturellement dans l'étude des réseaux de Bravais. Tout d'abord, comme dans un espace vectoriel, le réseau forme un groupe pour l'addition des vecteurs. Ce groupe est isomorphe au groupe des translations laissant le réseau invariant. Ensuite, une question importante est celle du groupe orthogonal, appelé parfois groupe ponctuel de symétrie. Il est composé des applications linéaires qui conservent les distances et les angles, à l'image d'une rotation ou d'une réflexion dans un miroir. Ces transformations forment les isométries vectorielles du réseau. Dans un réseau, le groupe orthogonal est toujours fini et dispose d'une structure de groupe. C'est-à-dire qu'il existe un élément neutre, celui qui ne bouge aucun point du réseau, que l'application réciproque d'une isométrie est encore une isométrie et que la loi de composition des applications linéaires est associative. Enfin, en combinant les deux groupes précédents, on peut former un autre groupe : le groupe d'espace du réseau.

Contrairement au cas des espaces vectoriels, les groupes orthogonaux de deux réseaux de même dimension ne sont pas forcément isomorphes. Élucider la structure du groupe orthogonal d'un réseau de dimension 2 est relativement aisé. Il n'existe que 4 groupes finis possibles et ils sont tous de petits cardinaux : 2, 4, 8 ou 12. Aucun outil sophistiqué n'est nécessaire, il suffit d'utiliser quelques matrices 2x2 pour arriver à ses fins. En dimension 3, la question se corse un petit peu. Le groupe le plus vaste contient 48 éléments. Pour expliciter la structure d'un groupe, il est plus simple de faire appel à la théorie des représentations d'un groupe fini. Un outil un peu abstrait, le caractère permet de résoudre rapidement des questions, d'apparence délicate.

L'article détaillé Réseau (géométrie) fait usage de l'algèbre linéaire pour construire les groupes orthogonaux des réseaux de dimension 2 et de la représentation d'un groupe pour la dimension 3.

Espace unidimensionnel

Dans l’espace à une dimension, il ne peut exister qu’un seul type de réseau, qui consiste en une répétition périodique de nœuds le long de la seule direction existante, indiquée comme axe a. La distance entre deux nœuds est le paramètre a.

• 
  Réseau de l'espace unidimensionnel.

Espace bidimensionnel

Dans l’espace à deux dimensions, la maille conventionnelle peut être primitive (p) ou centrée (c). Les axes sont indiqués par les lettres a et b, l’angle inter-axial est appelé γ. Cinq types de réseaux existent dans cet espace, qui sont indiqués par la lettre correspondant à la famille cristalline, suivie par le mode de réseau (en minuscule).

Famille cristalline monoclinique

Dans la famille cristalline monoclinique, il n’existe aucune restriction sur les paramètres. Un seul type de réseau existe dans cette famille : mp (monoclinique primitif).

• 
  Réseau monoclinique primitif de l'espace bidimensionnel.

Famille cristalline orthorhombique

Dans la famille cristalline orthorhombique, γ = 90°. Deux types de réseau existent : le réseau op (orthorhombique primitif) et le réseau oc (orthorhombique centré). Dans la figure qui montre la maille conventionnelle du réseau oc (rouge), quatre mailles primitives sont aussi visibles (noires).

• 
  Réseau orthorhombique primitif de l'espace bidimensionnel.
• 
  Réseau orthorhombique centré de l'espace bidimensionnel. La maille conventionnelle (rouge) et quatre mailles primitives (noires) sont montrées dans la figure.

Famille cristalline tétragonale (quadratique)

Dans la famille cristalline tétragonale^[1] a = b et γ = 90°. Un seul type de réseau existe dans cette famille : tp (tétragonal primitif).

• 
  Réseau tétragonal primitif de l'espace bidimensionnel.

Famille cristalline hexagonale

Dans la famille cristalline hexagonale a = b et γ = 120°. Un seul type de réseau existe dans cette famille : hp (hexagonal primitif).

• 
  Réseau hexagonal primitif de l'espace bidimensionnel.

Espace tridimensionnel

Les réseaux de l’espace tridimensionnel peuvent être obtenus à partir de ceux de l’espace bidimensionnel en ajoutant une troisième direction non-coplanaire. Les axes sont indiqués par a, b et c, les angles par α (entre b et c), β (entre a et c) et γ (entre a et b). Sept modes de réseau sont possibles, indiqués par une lettre majuscule :

• P : mode primitif, nœuds de réseaux seulement aux sommets de la maille ;
• A : un nœud de réseau au centre de la face A de la maille, définie par les axes b et c ;
• B : un nœud de réseau au centre de la face B de la maille, définie par les axes a et c ;
• C : un nœud de réseau au centre de la face C de la maille, définie par les axes a et b ;
• F : un nœud de réseau au centre de chaque face de la maille (la maille F est à la fois A, B et C) ;
• I : un nœud de réseau au centre du volume de la maille ;
• R : deux nœuds sur la diagonale majeure de la maille hexagonale.

La lettre S (une Seule paire de faces centrées) est aussi utilisée pour indiquer de manière collective les réseaux à une face centrée qui peuvent être transformés entre eux à la suite d'un changement d’axes.

Quatorze types de réseaux existent dans cet espace, qui sont indiqués par la lettre correspondant à la famille cristalline suivie par le mode de réseau (en majuscule).

Famille cristalline triclinique

Dans la famille cristalline triclinique il n’existe aucune restriction sur les paramètres. Un seul type de réseau existe dans cette famille : aP (anortique primitif). La lettre t étant réservée à la famille cristalline tétragonale, on utilise a (anortique, synonyme de triclinique).

• 
  Réseau triclinique primitif de l'espace tridimensionnel.

Famille cristalline monoclinique

Dans la famille cristalline monoclinique deux angles sur trois (normalement choisis comme α et γ) sont droits. Deux types de réseau existent dans cette famille : mP et mC. La maille mC peut être transformée en mI avec un choix différent des axes.

• 
  Réseau monoclinique primitif de l'espace tridimensionnel.
• 
  Réseau monoclinique C de l'espace tridimensionnel et sa description alternative par une maille mI.

Famille cristalline orthorhombique

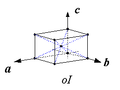
Dans la famille cristalline orthorhombique les trois angles sont droits. Quatre types de réseaux existent dans cette famille : oP, oS, oI et oF. Comme la symétrie de la maille conventionnelle n’impose aucune priorité sur les axes, les trois réseaux oA, oB et oC sont équivalents à la suite d'un changement des axes et sont indiqués collectivement comme oS.

• 
  Réseau orthorhombique primitif de l'espace tridimensionnel.
• 
  Réseau orthorhombique à une face centrée de l'espace tridimensionnel. Les trois réseaux oA, oB et oC peuvent être transformé l'un en l'autre avec des choix différents des axes et sont indiqués collectivement comme oS.
• 
  Réseau orthorhombique à volume centré de l'espace tridimensionnel.
• 
  Réseau orthorhombique à toute face centrée de l'espace tridimensionnel.

Famille cristalline tétragonale (quadratique)

Dans la famille cristalline tétragonale^[1] a = b, α = β = γ = 90°. Deux types de réseau existent dans cette famille : tP (équivalent à tC ) et tI (équivalent à tF).

• 
  Réseau tétragonal primitif de l'espace tridimensionnel. Le réseau tC est équivalent au réseau tP avec un choix différent des axes.
• 
  Réseau tétragonal à volume centré de l'espace tridimensionnel. Le réseau tF est équivalent au réseau tI avec un choix différent des axes.

Famille cristalline hexagonale

Dans la famille cristalline hexagonale a = b, α = β = 90°, γ = 120°. Deux modes de réseau existent dans cette famille : hP et hR.

• 
  Réseau hexagonal primitif de l'espace tridimensionnel.
• 
  Réseau rhomboédrique de l'espace tridimensionnel.

Famille cristalline cubique

Dans la famille cristalline cubique a = b = c, α = β = γ = 90°. Trois modes de réseau existent dans cette famille : cP, cI et cF.

• 
  Réseau cubique primitif de l'espace tridimensionnel.
• 
  Réseau cubique centré de l'espace tridimensionnel.
• 
  Réseau cubique à faces centrées de l'espace tridimensionnel.

Réseau centré ou maille centrée ?

Un réseau, étant une distribution régulière de nœuds dans l’espace, n'est ni primitif ni centré. L’expression « réseau primitif / réseau centré » est en effet un abus de langage pour « réseau dont la maille conventionnelle est primitive / centrée »^[2].

Note historique

Les réseaux de l’espace tridimensionnel furent déterminés par Moritz Ludwig Frankenheim (en) en 1842, qui ne reconnut pas l’équivalence des réseaux mC et mI. Auguste Bravais en 1848 corrigea l’erreur, en fixant à 14 le nombre correct.

Bibliographie

• Jean-Pierre Debard, « Les réseaux d’Auguste Bravais (1811-1863), une contribution décisive à la cristallographie : dans cahier consacré aux savants et ingénieurs d'Ardèche », Cahier de Mémoire d'Ardèche et Temps Présent, n^o 95,‎ 15 août 2007 (lire en ligne)

Notes

1. L’adjectif d'origine latine quadratique est plus utilisé en français que l'adjectif d'origine grecque tétragonal. Toutefois, ce dernier est l'adjectif standard utilisé dans les Tables internationales de cristallographie. Par ailleurs, les symboles des réseaux de Bravais dans cette famille utilisent la première lettre t de l'adjectif tétragonal.
2. (en) Sidney F.A. Kettle et Lars J. Norrby, « Really, your lattices are all primitive, Mr. Bravais! », Journal of Chemical Education, vol. 70, n^o 12,‎ 1993, p. 959-963. (DOI 10.1021/ed070p959)

Articles connexes

• Premier atome frappé

Sur les autres projets Wikimedia :

• Réseau de Bravais, sur Wikimedia Commons
• Réseau de Bravais, sur Wikibooks

• Portail de la chimie
• Portail des sciences des matériaux
• Portail des minéraux et roches