Mésomérie

En chimie, la mésomérie désigne une délocalisation d'électrons dans les molécules conjuguées, que l'on représente par une combinaison virtuelle de structures aux électrons localisés appelées mésomères ou formes de résonance. Faute de moyens graphiques plus simples pour les décrire correctement, la mésomérie est donc une représentation simplifiée des systèmes moléculaires, qui sont plus précisément décrits par des approches de chimie quantique. Le terme « mésomérie » est dû à Ingold. Il est préférable au terme synonyme de « résonance », proposé plus tôt par Pauling, car il n'y a pas en réalité de résonance (caractérisée par une fréquence de résonance), mais une superposition d'états^[1].

Mésomérie : un exemple de couple donneur-accepteur

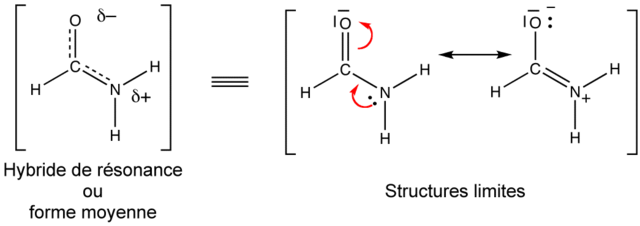
Insuffisance des formules de Lewis

On peut parfois écrire plusieurs formules de Lewis possibles pour un même assemblage d'atomes. Dans ces cas, la molécule n'est clairement pas décrite correctement par une seule de ces formes, qui sont nommées formes limites, mais par une combinaison, un hybride de ces formes. En invoquant ainsi plusieurs formules de Lewis, on peut rendre compte de certaines propriétés physiques (charges électroniques, polarité, distances interatomiques, couleur, etc.) et chimiques (stabilité, réactivité) de certains types de molécules. La mésomérie est symbolisée par une double flèche (${\displaystyle \longleftrightarrow }$), à ne pas confondre avec celle des équilibres (${\displaystyle \rightleftharpoons }$).

Les formules de Lewis contribuantes ayant leurs électrons localisés différemment, la mésomérie entre elles traduit à sa façon la délocalisation électronique. En chimie organique, il s'agit surtout d'électrons π et d'orbitales p, mais les orbitales d peuvent aussi participer dans les complexes de coordination et les composés organométalliques^[2].

Conception des mésomères

Doublets électroniques en chimie

Dans les systèmes conjugués, on parle de mésomérie lorsque dans une structure de Lewis, on a par exemple :

• une alternance doublet liant (π) - liaison simple (σ) - doublet liant (π), comme dans un diène conjugué,
• une alternance doublet libre - liaison simple (σ) - doublet liant (π), comme dans un éther vinylique,
• un couple doublet libre - liaison simple (σ) - orbitale p vide, comme dans le borazole (B₃N₃H₆),
• un couple doublet liant (π) - liaison simple (σ) - orbitale p vide, comme dans l'ion allyle (CH₂=CH-CH₂⁺),
• une alternance électron libre - liaison simple (σ) - doublet liant (π), comme dans le radical benzyle,

On passe d'une forme mésomère à une autre en utilisant une flèche courbée pour indiquer le déplacement d'un doublet d'électrons (libre ou liant) ou par une cascade de telles flèches, ou des demi-flèches indiquant le déplacement d'un seul électron dans le cas des radicaux, pour établir ou défaire des liaisons π. Les exemples ci-bas sont illustratifs. La séquence des flèches n'est pas importante. Toutefois, la mésomérie impose de ne casser aucune liaison σ (sigma) pour passer d'une forme à une autre^[3]. Dans le cadre de la mésomérie, les liaisons σ peuvent être vues comme définissant un squelette sur lequel se déplacent les électrons π.

L'importance de la contribution de chaque mésomère à la structure réelle peut varier, puisque certaines formulations seront nécessairement plus énergétiques, à cause d'un nombre inférieur de liaisons chimiques par exemple, et donc moins probables que d'autres. On considère alors que certaines structures seront « majoritaires » et d'autres « minoritaires » et que la structure réelle sera une moyenne pondérée de toutes les structures contribuantes, mais ressemblant plus aux structures « majoritaires » et moins aux autres. On attribue donc aux formes mésomères une « probabilité » ou « poids », selon certaines caractéristiques. Contribueront plus les mésomères qui :

• respectent le plus possible la règle de l'octet (on préfère avoir 8 électrons autour de chaque atome plutôt que des lacunes ou des hypervalences),
• sont dotés d'un minimum de charges électriques (on préfère une structure entièrement neutre à une structure faisant apparaître une séparation de charge +/-),
• placent les charges électriques sur les atomes les plus aptes à les soutenir (une charge négative sur un atome électronégatif et réciproquement).

La structure réelle est alors une combinaison linéaire de ces structures contribuantes, dont l'apport de chacune est évalué de manière qualitative selon ces caractéristiques et qui s'apparente à sa stabilité.

Exemples

Mésomérie du benzène

• Le benzène : Un exemple classique est donné par les formes de Kékulé du benzène (un hexagone comportant 3 double-liaisons). La molécule de benzène est faite d'un hexagone parfait d'atomes de carbone, avec 6 liaisons carbone-carbone identiques, et non une alternance de liaisons doubles plus courtes (134pm) et de liaisons simples plus longues (154pm), comme le laisseraient penser les deux formes limites prises séparément. Les deux mésomères majoritaires sont identiques et de même poids, et la longueur des liaisons C-C, trouvée expérimentalement, est intermédiaire entre celles d'une liaison simple et d'une liaison double (139 pm)^[4]. C'est la raison pour laquelle on représente souvent le benzène, ou un de ses dérivés, par un hexagone contenant un cercle ou, plus rarement, par un hexagone contenant 6 «liaisons et demi » (une liaison avec une demi-liaison en pointillé).

Les formes mésomères de l'ion acétate ainsi qu'une structure hybride.

• L'ion acétate : L'acidité beaucoup plus grande des acides carboxyliques par rapport à celle des alcools est explicable en partie par la mésomérie. Par déprotonation, un alcool donne un alcoolate dont la charge ne peut pas être délocalisée, alors qu'un acide carboxylique donne un carboxylate pouvant présenter des formes mésomères avec distribution de la charge négative sur les deux atomes d'oxygène, ce qui confère plus de stabilité^[5]. L'atome d'oxygène chargé porte trois doublets et agit en donneur π, alors que l'autre oxygène est accepteur π^{[réf. nécessaire]}. Ici aussi, les deux mésomères majoritaires sont identiques, ils ont le même poids et on peut alors correctement prédire que les liaisons carbone-oxygène seront identiques et de longueur intermédiaire entre celles d'une liaison simple et d'une liaison double (ce que l'on représente souvent par une deuxième liaison hachurée).

On utilise des demi-flèches pour indiquer le mouvement d'électrons solitaires.

• Le radical allylique : Comme dans les cas de l'acétate et du benzène, les formes mésomères de ce radical sont identiques. Ce radical jouit d'une stabilité accrue, en comparaison avec d'autres, parce que l'électron solitaire est distribué et l'octet incomplet est partagé.

Énol et énolate : mésomérie de la base conjuguée.

• Les énolates : Ces espèces sont les bases conjuguées des énols, qui bénéficient, comme l'acétate, d'une stabilisation par mésomérie. Par contre, les deux mésomères ne sont pas de poids égaux, étant donné la plus grande électronégativité de l'oxygène, et cette stabilisation n'est pas grande (les acidités des alcools et des énols sont plutôt voisines). Toutefois, la mésomérie sert à expliquer la réactivité ambidente des énolates, qui réagissent en tant que nucléophiles à l'oxygène ou au carbone, selon les conditions de la réaction.

Mésomères et leur échange.

• L'ion cyanate : La mésomérie dans ce cas explique sa réactivité ambidente, car cet ion peut donner lieu à des composés cyanates et isocyanates par réaction de l'azote ou de l'oxygène, selon les conditions.

• Les amides : L'azote, avec son doublet libre, est un donneur π et l'oxygène est accepteur π; (car sp²). Il en découle une double liaison partielle entre N et C, qui explique la rigidité de cette liaison vis-à-vis de la rotation (15 kcal/mol ou 60 kJ/mol environ de barrière énergétique), et une liaison C=O affaiblie, ce qui explique l'absorption en infrarouge par le groupement carbonyle à plus grande longueur d'onde par rapport à une cétone. Cette mésomérie explique aussi le fait que l'azote dans un amide est beaucoup moins basique que dans une amine, puisque son doublet est partiellement délocalisé, et que quand un amide réagit avec un électrophile, c'est l'atome d'oxygène qui agit en nucléophile.

Ce que la mésomérie n'est pas

La double flèche ${\displaystyle \longleftrightarrow }$ qui symbolise la mésomérie, les flèches courbées qui montrent les déplacements électroniques qui génèrent un mésomère à partir d'un autre, et le terme malencontreux résonance suggèrent tous un va-et-vient entre formes limites, une sorte de vibration apparentée au phénomène physique de résonance, comme l'avait imaginé Kekulé. Cependant, un tel échange dynamique serait associé à une énergie et pourrait en principe être ralenti ou même arrêté, alors que le concept moderne de mésomérie est strictement statique et nie tout déplacement.

Rapport avec la stabilité

La mésomérie est une figuration de la délocalisation qui peut servir à expliquer ce qu'une seule formule de Lewis ne peut pas expliquer, mais elle n'explique pas le pourquoi de la délocalisation. Quand une mésomérie est nécessaire pour expliquer quelque chose, on est porté à croire que la mésomérie est stabilisante. En effet, la règle générale stipule que, pour un type d'espèce chimique donné, l'espèce avec plus de mésomères sera plus stable qu'une autre avec moins de mésomères. Mais cette règle ne permet pas de comparer un mésomère « majoritaire » avec un « minoritaire », et il est impossible de quantifier la stabilisation. Bien que l'on puisse concevoir des « poids » relatifs pour chaque forme majoritaire ou minoritaire, on ne peut pas représenter ces poids, et la mésomérie ne précise pas non plus la distribution électronique de la structure hybride.

La théorie des orbitales moléculaires permet la quantification de la stabilisation qui résulte d'une délocalisation, de visualiser et de préciser la distribution électronique résultante, ainsi que de mesurer les distances et angles interatomiques. Le mélange d'orbitales atomiques par recouvrement dans l'espace crée des orbitales dites moléculaires, liantes, non-liantes et anti-liantes, qui expliquent non seulement les liaisons π (et autres), mais aussi la stabilisation par conjugaison. Cette théorie peut aussi décrire l'hyperconjugaison, ce que les formes mésomères traduisent avec difficulté.

Calculs des poids

Le calcul des poids des formes mésomères peut se faire de différentes façons, ab initio avec des méthodes dérivées de Valence Bond, ou avec une méthode dérivée des approches Natural Bond Orbital (NBO) de Weinhold NBO5, qui procède essentiellement par projection de la densité électronique délocalisée sur les formes localisées représentatives des structures de Lewis.

On peut aussi accéder à ces poids par des calculs empiriques (Hückel). Un logiciel destiné à l'étude des poids de la mésomérie basé sur la méthode de Hückel est disponible sur le site de HuLiS

Notes et références

1. (en) « More on the nature of resonance »
2. Le concept de mésomérie a permis de décrire qualitativement de façon satisfaisante de nombreux exemples parmi ces derniers types de molécules, avant la large diffusion des approches de chimie numérique pour l'étude des structures moléculaires. On peut aussi dire que les liaisons σ peuvent être rompues dans des formes mésomères pour exprimer la dichotomie liaison covalente - liaison ionique, sauf dans le cas d'un lien entre atomes identiques.
3. Certains, par exemple Wade, exigent aussi qu'il n'y ait pas de déplacement des noyaux atomiques, et donc pas de changements dans les états d'hybridation des atomes (car ceci engendrerait un changement de géométrie et donc des changements de position des atomes liés). Toutefois ce genre de déplacement est recevable, puisqu'on admet qu'il y ait des liaisons doubles et courtes qui deviendront simples et plus longues dans une forme mésomèrique, et vice versa. Donc, dans le cas d'un amide, par exemple, on peut formuler un mésomère avec un azote sp³ tandis que l'autre est sp² ; la forme hybride réelle sera quelque part entre les deux, avec un azote moins pyramidal qu'un sp³ pur (à géométrie tétraédrique parfaite), mais moins plat qu'un sp² pur (à géométrie trigonale parfaite). Les hybrides sp³ et sp² que l'on mélange pour faire des orbitales moléculaires π (et qui ne sont eux-mêmes que des mélanges d'orbitales atomiques s et p) donnent une hybridation intermédiaire entre sp³ pur et sp² pur ; cette nouvelle combinaison d'orbitales atomiques serait normalement moins stable, mais, dans le cas d'un amide, il permet une interaction avec le système π de la fonction carbonyle voisine, ce qui est stabilisant.
4. Atkins, Peter William (1940-....), Jones Loretta et Pousse, André (1939-....). (trad. de l'anglais), Chimie : molécules, matière, métamorphoses, Paris/Bruxelles, De Boeck université, impr. 1998, cop. 1998, 1018 p. (ISBN 2-7445-0028-3 et 9782744500282, OCLC 489879525, lire en ligne), p. 281
5. L'acidité accrue est aussi due à la présence d'un deuxième atome électronégatif.

Bibliographie

• (en) L. Pauling The Nature of the Chemical Bond, Cornell University Press (ISBN 0801403332) ;
• (en) L. G. Wade, Jr. Organic Chemistry, 6th ed. Prentice-Hall, 2006 (ISBN 0-13-169957-1).

• Portail de la chimie