Interconnexions entre la théorie des probabilités et la statistique

Les interconnexions entre la théorie des probabilités et la statistique (la science des statistiques) montrent les liens et différences entre ces deux domaines mathématiques qui forment les sciences de l'aléatoire ^[1]. Ces sciences sont en interaction avec les autres disciplines mathématiques mais aussi avec les sciences physiques, les sciences économiques et les sciences du vivant, etc.

Dans ce logo, les histogrammes sont une représentation de données statistiques, la courbe de Gauss est la fonction de densité d'une loi de probabilité qui approche (modélise) ces données.

Donnons de premières définitions générales : la théorie des probabilités est l'étude mathématique des phénomènes caractérisés par le hasard et l'incertitude ; la statistique consiste à recueillir, traiter, interpréter et présenter un ensemble de données.

Homonymies

Classons les homonymies de probabilités et statistique par domaine.

En probabilités

• La théorie des probabilités (parfois appelée « les probabilités »^[2],[3], « probabilité mathématique »^[4] ou « calcul des probabilités »^[5]) est le domaine mathématique des phénomènes caractérisés par le hasard et l'incertitude.
• Une probabilité est l'évaluation du caractère probable d'un événement.

• Dans l'article probabilités (mathématiques élémentaires), on présente la notion de probabilité et les premiers outils utiles dans ce domaine.
• La probabilité conditionnelle d'un événement est la probabilité de cet événement sachant qu'un autre événement se produit.
• Les termes probabilité a priori et probabilité a posteriori sont utilisés dans le domaine de l'inférence bayésienne pour désigner un calcul de probabilités avant ou après une expérience.

En statistique

Dans le langage courant, les statistiques en mathématiques élémentaires sont les résultats d'une enquête qui consiste à observer une certaine population et à déterminer la répartition d’un certain caractère statistique (taille, nombre d’enfants, superficie,…) dans cette population.

• La statistique^[3] (notées également statistiques et parfois appelée probabilité statistique^[4] ou statistique mathématique^[5]) est le domaine mathématique qui consiste à recueillir, traiter et interpréter un ensemble de données. À noter que les termes les statistiques ou l'étude des statistiques sont parfois utilisés (par abus de langage) pour ce domaine mathématique.
• Une statistique^{[notes 1]} (des statistiques au pluriel) est une quantité calculée à partir d'un certain nombre d'observations (ou échantillon). On parle également de donnée statistique.

• L'inférence statistique (ou statistique inférentielle) est un ensemble de méthodes permettant de tirer des conclusions fiables à partir de données d'échantillons statistiques. L'interprétation de données statistiques est, pour une large part, le point clé de l'inférence statistique.
• La statistique descriptive est la branche des statistiques qui regroupe les nombreuses techniques utilisées pour décrire un ensemble relativement important de données.
• Les statistiques élémentaires continues constituent un domaine des mathématiques élémentaires qui traite le cas où, dans une enquête statistique, le caractère statistique est une valeur continue.
• Les statistiques élémentaires discrètes constituent un domaine des mathématiques élémentaires qui traite le cas où, dans une enquête statistique, le caractère statistique prend un nombre fini raisonnable de valeurs.
• La statistique « mathématique » est la branche des statistiques où le défi est de trouver des estimateurs judicieux (non biaisés et efficients). L'analyse des propriétés mathématiques de ces estimateurs sont au cœur du travail du mathématicien spécialiste de la statistique.

En probabilités et statistique

• Une loi de probabilité décrit soit les probabilités de chaque valeur d'une variable aléatoire discrète, soit la probabilité que la variable aléatoire continue appartienne à un intervalle arbitraire. C'est la caractérisation d'un phénomène aléatoire. Les lois de probabilités sont étudiées en théorie des probabilités et sont utilisées en statistique.

Définitions plus détaillées

• En théorie des probabilités, les probabilistes s'intéressent aux issues théoriques d'une expérience régie par de l'aléatoire, aléatoire que l'on modélise par des lois adéquates, des lois qu'on estime correspondre au modèle réel. On peut parler d'une « connaissance a priori »^[6] puisque l'étude se fait sans données.

«  À mon avis la théorie des probabilités est une discipline tout à fait du même genre que la géométrie ou la mécanique rationnelle. Elle a pour but la description systématique de certains phénomènes réels et se sert d'une construction idéalisée des notions et définitions abstraites.  »

— Richard von Mises, 1932^[4]

• En statistique, les statisticiens étudient des données empiriques (c'est-à-dire des données issues de situations concrètes). En les recueillant (lors d'un sondage par exemple), en les analysant qualitativement et/ou quantitativement (par des tableaux de données par exemple), en les interprétant pour leur trouver des propriétés, puis en les extrapolant pour émettre des hypothèses sur les données futures.
  On peut parler d'une « connaissance a posteriori »^[6] puisque l'étude se fait après collecte de données.
  • Certains utilisent le terme « probabilité statistique »^[6] pour désigner la statistique. Dans ce cas, la statistique est considérée comme une branche de la théorie des probabilités.
  • Pour analyser les données statistiques, des outils probabilistes sont utilisés (comme l'espérance mathématique ou la variance), certains considèrent alors que la théorie des probabilités n'est qu'un outil pour la statistique.

«  La statistique est un mode de pensée permettant de recueillir, de traiter et d’interpréter les données qu’on rencontre dans divers domaines, et tout particulièrement dans les sciences de la vie, du fait que ces données présentent une caractéristique essentielle : la variabilité.  »

— Daniel Schwartz, 1994

Ici nous considérons que les probabilités et la statistique sont deux domaines des sciences de l'aléatoire qui sont en interaction l'une avec l'autre.

«  La théorie des probabilités et la statistique sont deux domaines importants, intégrés à nos activités quotidiennes. Le monde de l’industrie, les compagnies d’assurance sont largement tributaires des lois probabilistes. La physique elle-même est de nature essentiellement probabiliste. Il en est de même des fondements de la biologie.  »

— Warren Weaver, 1963^[7]

«  Vous avez voulu témoigner que les statisticiens ne regardaient pas les mathématiciens comme des frères ennemis : soyez assurés que ces bons sentiments sont réciproques.  »

— Émile Borel, extrait de son discours inaugural pour la présidence de la SSP en 1922

Liens à travers un exemple

Prenons un exemple simple : celui du jeu de pile ou face.

Une question statistique serait : La pièce est-elle équilibrée? C'est-à-dire, plus mathématiquement, La probabilité d'obtenir pile est-elle 1/2? (voir cette section)

Détaillons le déroulement d'un test statistique. On commence par se fixer une hypothèse statistique : (H0) La probabilité d'obtenir pile est 1/2. On se donne également un risque seuil, c'est-à-dire un pourcentage en dessous duquel on accepte de rejeter H0. Par exemple on accepte que dans 5 % des cas où H0 est vraie, le test affirme que H0 est fausse. On se fixe un nombre significatif d'expériences à réaliser pour que le test statistique soit valide (voir par exemple cette section). Ce nombre doit être suffisamment petit pour être réalisable. On réalise les expériences et on recueille les résultats, c'est-à-dire que l'on compte la fréquence du résultat pile. On utilise alors un test statistique pour comparer cette valeur empirique avec la vraie valeur espérée : 1/2. On conclut sur l'acceptation ou le refus de H0 en fonction du seuil fixé.

• 
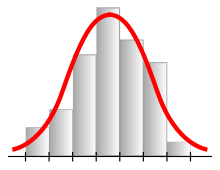
  Proportion de face dans un jeu de pile ou face. Pour chacun des 10 000 jeux de 200 lancers, on compte la proportion de face.
• 
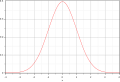
  Courbe, dite « en cloche », de la loi normale qui est la représentation théorique de la fréquence de face.

Pour une étude probabiliste, on considère que la probabilité d'obtenir pile est 1/2. Puis on étudie une loi de probabilité ou la valeur d'une probabilité à partir du jeu aléatoire. Par exemple : Lorsque l'on réalise une infinité de lancers de pile ou face, quelle est la probabilité d'obtenir uniquement le résultat pile? (voir cette section)

Dans ce cas, on connait déjà la loi de probabilité associée au jeu de pile ou face. Par la loi du zéro un de Kolmogorov on sait que cette probabilité vaut soit 0 soit 1. Elle vaut donc 0 puisque son complémentaire (obtenir au moins une fois face) est de probabilité positive.

Autre question probabiliste : Si N désigne le numéro du premier lancer auquel apparait pile pour la première fois, quelle est la loi de N?

Connaissant l'indépendance des lancers et la probabilité d'obtenir pile (1/2), on déduit que cette loi est une loi géométrique. C'est-à-dire que la probabilité que N soit k est ${\displaystyle \scriptstyle 1/2^{k}}$ (1/2 pour N=1, 1/4 pour N=2, 1/8 pour N=3, etc) .

Notes et références

Notes

1. La différence ici est l'utilisation de une au lieu de la.

Références

1. « Probabilités et Statistique, vers une nouvelle place dans le monde de demain : une table ronde animée par Étienne Pardoux », 2010.
2. « site web de la Société française de statistique » (consulté le 4 octobre 2011)
3. Alan Rueg, Probabilités et statistique, Presses polytechniques et universitaires romandes, 1994, 4^e éd., 267 p. (ISBN 2-88074-286-2, lire en ligne), Avant-propos
4. Richard von Mises, Théorie des Probabilités. Fondement et applications, annales de l'IHP, tome 3 n°2 (1932), p137-190.
5. « Site du Conseil National des Universités, section 26 » (consulté le 4 octobre 2011)
6. termes a priori et a posteriori, voir également cette sous-section
7. Jean-Claude Régnier, Finalités et enjeux de l’enseignement de la statistique, halshs-00405986, version 1 - 23 Jul 2009.

• Portail des probabilités et de la statistique