Fonction de Dawson

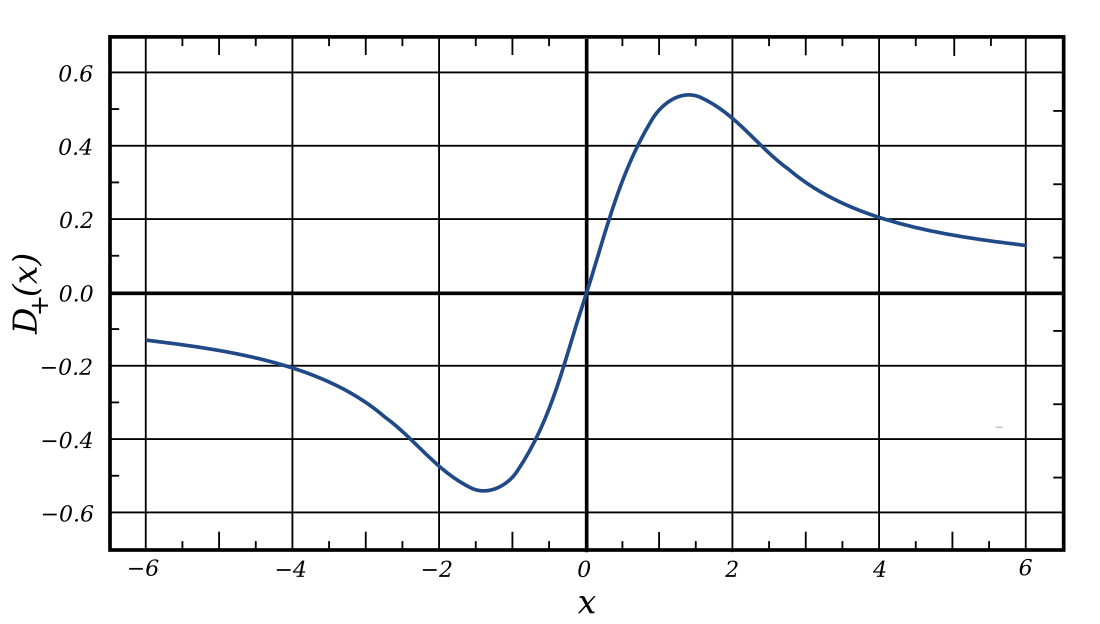
En mathématiques, et plus précisément en analyse, la fonction de Dawson (portant le nom de H. G. Dawson, et parfois appelée intégrale de Dawson) est une fonction spéciale, définie comme étant une solution particulière de l'équation différentielle

${\displaystyle y'+2xy=1.}$

La fonction de Dawson, ${\displaystyle F(x)}$, près de l'origine.

Une fonction de Dawson généralisée, ${\displaystyle D_{-}(x)}$, près de l'origine.

Définition et propriétés

La fonction de Dawson peut être définie comme la solution de l'équation différentielle

${\displaystyle F'(x)+2xF(x)=1}$

satisfaisant la condition initiale  F(0) = 0 ; la méthode de variation de la constante permet alors d'en déduire que

${\displaystyle F(x)={\rm {e}}^{-x^{2}}\int _{0}^{x}{\rm {e}}^{t^{2}}\,{\rm {d}}t.}$

La fonction de Dawson peut être calculée à partir de la fonction d'erreur erf : on a

${\displaystyle F(x)={{\sqrt {\pi }} \over 2}{\rm {e}}^{-x^{2}}\mathrm {erfi} (x)=-{{\rm {i}}{\sqrt {\pi }} \over 2}{\rm {e}}^{-x^{2}}\mathrm {erf} ({\rm {i}}x)}$

où erfi est la fonction d'erreur imaginaire, erfi(x) = −i erf(ix).

Quand x tend vers 0, on a ${\displaystyle F(x)\sim x}$ (au sens de l'équivalence des fonctions) et quand x tend vers l'infini, ${\displaystyle F(x)\sim {\frac {1}{2x}}}$.

Plus précisément, au voisinage de 0, le développement en série entière de F est :

${\displaystyle F(x)=\sum _{n=0}^{+\infty }{\frac {(-2)^{n}}{1\cdot 3\cdot 5\cdots (2n+1)}}\,x^{2n+1}=x-{\frac {2}{3}}x^{3}+{\frac {4}{15}}x^{5}-\dots }$

(cette série entière converge pour tout x) et, son développement asymptotique en ${\displaystyle +\infty }$ est :

${\displaystyle F(x)={\frac {1}{2x}}+{\frac {1}{4x^{3}}}+{\frac {3}{8x^{5}}}+\dots +{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{2^{n+1}x^{2n+1}}}+o(x^{-2n-2})}$

(qui, au contraire, correspond pour tout x à une série divergente).

Généralisations

On trouve parfois pour la fonction de Dawson la notation ${\displaystyle D_{+}(x)={\rm {e}}^{-x^{2}}\int _{0}^{x}{\rm {e}}^{t^{2}}\,{\rm {d}}t}$, et la fonction « symétrique » est alors notée ${\displaystyle D_{-}(x)={\rm {e}}^{x^{2}}\int _{0}^{x}{\rm {e}}^{-t^{2}}\,{\rm {d}}t}$ ; avec ces notations, on a donc ${\displaystyle D_{+}(x)={{\sqrt {\pi }} \over 2}{\rm {e}}^{-x^{2}}\mathrm {erfi} (x)\quad {\rm {et}}\quad D_{-}(x)={{\sqrt {\pi }} \over 2}{\rm {e}}^{x^{2}}\mathrm {erf} (x).}$

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Dawson function » (voir la liste des auteurs).

Liens externes

• Cephes - Bibliothèque de programmes de calcul de fonctions spéciales en C et C++
• (en) Eric W. Weisstein, « Dawson's Integral », sur MathWorld
• (en) Nikolai G. Lehtinen, « Error functions », sur Université Stanford, 2010

• Portail de l'analyse