Système oscillant à un degré de liberté

Les phénomènes physiques dépendant du temps sont généralement décrits au départ par des équations différentielles. Dans le cas le plus simple, il y a une seule grandeur qui varie et on parle de système à un degré de liberté, la plupart du temps régi par une équation différentielle du second ordre. Les phénomènes naturels sont presque toujours non-linéaires mais, dans de nombreux cas, l'hypothèse des petits mouvements permet d'aboutir à une excellente approximation fournie par une équation différentielle linéaire à coefficients constants d'ordre deux. Cet article a pour but de donner une interprétation physique de la théorie correspondante.

Généralités

Système masse-ressort

En mécanique, cette équation concerne particulièrement le système masse-ressort constitué par une masse accrochée à un ressort et contrainte de se déplacer dans une seule direction. Son mouvement est dû à trois forces :

• une force de rappel F_R,
• une force d'amortissement F_A,
• une force extérieure F_E.

M étant la masse et x sa position comptée à partir de l'équilibre, l'équation du mouvement s'écrit alors

${\displaystyle M{\ddot {x}}=F_{R}+F_{A}+F_{E}}$

Nota : voir le nota ci-dessous pour la signification des notations ${\displaystyle {\dot {x}}}$ et ${\displaystyle {\ddot {x}}}$.

La force de rappel est une fonction de la position qui varie en sens inverse de l'excursion, tout en passant par l'origine lorsque les excursions sont comptées à partir du point d'équilibre. Si on suppose qu'elle est fournie par un ressort hélicoïdal, au-delà d'une certaine extension le ressort se détend et l'allongement varie beaucoup plus vite que la tension. Inversement, au-delà d'une certaine compression les spires deviennent jointives et il faut fournir des efforts considérables pour faire varier la longueur. En se plaçant dans le cas des petits mouvements, la fonction compliquée ainsi obtenue se réduit à une fonction linéaire dans laquelle K est la raideur du système (Loi de Hooke) :

${\displaystyle F_{R}=-Kx\,}$

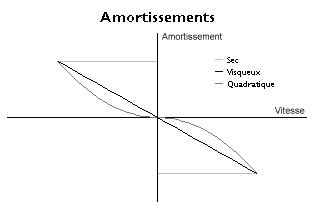
En ce qui concerne l'amortissement, qui dépend de la vitesse, on peut rencontrer un amortissement quadratique produit par les tourbillons ou la turbulence dans un fluide ou un frottement sec entre deux solides, à peu près indépendant de la vitesse. Néanmoins, à l'aide d'un raisonnement analogue au précédent, on est souvent amené à considérer un amortissement linéaire. Celui-ci s'observe en particulier dans un fluide, lorsque la vitesse est suffisamment faible pour que la viscosité ne soit plus négligeable (voir Nombre de Reynolds). On a alors, B étant le coefficient d'amortissement :

${\displaystyle F_{A}=-B{\dot {x}}}$

Enfin, la force extérieure peut être représentée par n'importe quelle fonction du temps f(t), ce qui conduit à l'équation

${\displaystyle M{\ddot {x}}+B{\dot {x}}+Kx=f(t)}$

Nota : la notation ${\displaystyle {\dot {x}}}$ signifie dx(t)/dt, dérivée par rapport au temps de la fonction x(t), c'est-à-dire la vitesse de la masse M.

De même ${\displaystyle {\ddot {x}}}$ = d²x/dt² est la dérivée seconde par rapport au temps de x, c'est-à-dire l'accélération de la masse M.

Systèmes analogues

On trouve une équation analogue dans d'autres problèmes de mécanique comme celui du pendule décrit par sa masse M, son moment d'inertie I, un coefficient d'amortissement B, la distance l de son centre de gravité à l'axe de rotation et un moment excitateur m(t). Si θ représente l'excursion angulaire, l'équation du mouvement s'écrit

${\displaystyle I{\ddot {\theta }}+B{\dot {\theta }}+Mgl\sin \theta =m(t)}$

Si on s'en tient aux petits mouvements, l'équation se réduit à

${\displaystyle I{\ddot {\theta }}+B{\dot {\theta }}+Mgl\theta =m(t)}$

Cette équation est identique à celle du système masse-ressort.

En électricité on trouve aussi une équation du même type pour un circuit comportant une auto-inductance L, une résistance R, une capacité C. La quantité d'électricité q engendrée par une tension v(t) est donnée par

${\displaystyle L{\ddot {q}}+R{\dot {q}}+q/C=v(t)}$

Problèmes particuliers considérés

Dans les équations ci-dessus, les coefficients sont tous positifs, ce qui, comme on le verra plus loin, assure la stabilité du système sans laquelle il serait sans grand intérêt d'exprimer les solutions en détail.

En ce qui concerne la force excitatrice du second membre on est amené à considérer deux types de problèmes. Si ce second membre est nul, il s'agit d'oscillations libres obtenues en écartant le système de sa position d'équilibre.

À l'opposé, une excitation non nulle crée des oscillations forcées qui subsistent seules après l'extinction des oscillations libres due à l'amortissement. Le problème de base concerne l'excitation sinusoïdale. Celui-ci est non seulement intéressant en lui-même mais la linéarité du système permet aussi, grâce aux techniques d'analyse spectrale, d'étendre les résultats obtenus à des excitations beaucoup plus compliquées considérées comme des sommes de sinusoïdes.

Enfin, bien que le mouvement perpétuel ne puisse exister, toute oscillation non entretenue s'éteignant plus ou moins rapidement, il est commode dans certaines circonstances de négliger l'amortissement et de distinguer les systèmes conservatifs des systèmes dissipatifs.

Oscillations libres

Systèmes conservatifs

Solution mathématique

L'équation d'un système sans amortissement écarté de sa position d'équilibre s'écrit donc

${\displaystyle M{\ddot {x}}+Kx=0}$

Selon la méthode décrite dans l'article précité sur les équations du second ordre, on cherche une solution de la forme x = e^rt, ce qui conduit à l'équation caractéristique

${\displaystyle Mr^{2}+K=0\,}$

Cette équation possède deux racines imaginaires conjuguées. On peut remarquer au passage que, si la «raideur» K était négative, on obtiendrait deux racines réelles de signes opposés, la valeur positive entraînant une instabilité du système.

La solution générale s'écrit

${\displaystyle x=C_{1}e^{i{\sqrt {K/M}}\,t}+C_{2}e^{-i{\sqrt {K/M}}\,t}}$

En utilisant les formules d'Euler, cette équation devient

${\displaystyle x=a\cos {\sqrt {K/M}}\,t+b\sin {\sqrt {K/M}}\,t}$

Solution en termes physiques

En posant a = A cos φ et b = -A sin φ, on obtient

${\displaystyle x=A\cos({\sqrt {K/M}}\,t+\phi )}$

Le mouvement est représenté par une sinusoïde définie par une amplitude A, une phase φ et une pulsation exprimée en radians par seconde, dite pulsation propre, qui ne dépend que de la masse et la raideur du système :

${\displaystyle \omega _{0}={\sqrt {K \over M}}}$

On en déduit la fréquence propre, nombre d'oscillations par seconde exprimé en hertz (Hz) :

${\displaystyle f={\omega _{0} \over {2\pi }}={1 \over {2\pi }}{\sqrt {K \over M}}}$

et la période propre, durée en secondes d'une oscillation :

${\displaystyle T={1 \over f}=2\pi {\sqrt {M \over K}}}$

L'une ou l'autre de ces trois grandeurs constitue l'information essentielle sur le système. Il est bon de remarquer que, quel que soit ce système, une augmentation de la masse accroît la période tandis qu'une augmentation de la raideur accroît la fréquence.

Solution en fonction des conditions initiales

Les deux autres constantes peuvent s'interpréter en fonction de la position x₀ et la vitesse v₀ initiales. D'une manière générale, elles peuvent être prises en compte en utilisant la transformation de Laplace mais, dans ce cas précis, le calcul direct à partir de la première expression réelle est plus simple. On obtient :

${\displaystyle x=x_{0}\cos \omega _{0}t+{v_{0} \over \omega _{0}}\sin \omega _{0}t}$

Solution en termes énergétiques

D'un point de vue énergétique, on calcule le travail des deux forces d'inertie et de rappel entre l'instant 0 et l'instant t par des formules du type

${\displaystyle \int _{x_{0}}^{x}F\,dx=\int _{t_{0}}^{t}F\,{\dot {x}}\,dt}$

En faisant passer au second membre les termes constants, on obtient

${\displaystyle {1 \over 2}M{\dot {x}}^{2}+{1 \over 2}Kx^{2}={1 \over 2}M{v_{0}}^{2}+{1 \over 2}K{x_{0}^{2}}}$

L'énergie totale du système, somme de l'énergie cinétique et de l'énergie potentielle, reste constamment égale à celle qui lui a été fournie en l'écartant de sa position d'équilibre. On parle de système conservatif qui n'existe pas dans la réalité car, dans tous les cas, l'énergie se dissipe à travers des phénomènes variés : il ne peut y avoir de mouvement perpétuel.

Systèmes dissipatifs

Solution mathématique

Dans un système réel, l'équation différentielle devient

${\displaystyle M{\ddot {x}}+B{\dot {x}}+Kx=0}$

et son équation caractéristique

${\displaystyle Mr^{2}+Br+K=0\,}$

Il y a maintenant deux racines réelles ou complexes selon le signe du discriminant B² - 4 K M. Dans les deux cas, elles ont une partie réelle négative, ce qui fait tendre la fonction vers 0.

Si le coefficient d'amortissement B reste faible on a, par continuité avec le cas précédent, deux racines complexes conjuguées qui conduisent à une solution oscillante mais amortie. Les amortissements élevés qui rendent le discriminant positif interdisent toute oscillation.

Solution en termes physiques

Les formules se simplifient en utilisant la pulsation propre ω₀ du système non amorti et le paramètre β défini par 2 β ω₀ = B / M. Pour β < 1, il vient

${\displaystyle x=Ae^{-\beta \omega _{0}t}\cos \left({\sqrt {1-\beta ^{2}}}\omega _{0}t+\varphi \right)}$

La pseudo-période de cette sinusoïde amortie est d'autant plus longue que l'amortissement est plus élevé. Lorsque β devient supérieur à 1, elle cesse d'exister et l'on a la solution

${\displaystyle x=ae^{(-\beta +{\sqrt {\beta ^{2}-1}})\omega _{0}t}+be^{(-\beta -{\sqrt {\beta ^{2}-1}})\omega _{0}t}}$

Solution en termes énergétiques

Le terme d'amortissement ne peut être intégré a priori. En le faisant passer dans le second membre, on obtient

${\displaystyle {1 \over 2}M{\dot {x}}^{2}+{1 \over 2}Kx^{2}={1 \over 2}M{v_{0}}^{2}+{1 \over 2}K{x_{0}^{2}}-\int _{0}^{t}B{\dot {x}}^{2}\,dt}$

L'énergie totale du système diminuant constamment, le nouveau terme s'appelle fonction de dissipation. On peut remarquer qu'un « amortissement » négatif créerait de l'énergie.

Q ou facteur de qualité

Pour décrire l'amortissement d'un système oscillant mécanique ou électrique on emploie le facteur de qualité ou simplement le Q du système. Dans le système mécanique précèdent, il est défini comme:

${\displaystyle Q={{\sqrt {KM}} \over B}}$

Un système très amorti a un ${\displaystyle Q}$ faible. À l'inverse, un ${\displaystyle Q}$ élevé correspond à un système peu amorti. Pour fixer les idées, le ${\displaystyle Q}$ d'une voiture avec des amortisseurs en bon état est légèrement supérieur à 1. Le ${\displaystyle Q}$ d'une corde de guitare est de quelques milliers. Celui des quartz utilisés en électronique pour fabriquer des oscillateurs stables est de l'ordre de quelques millions.

Avec les notations précédentes, il vient ${\displaystyle \beta =1/2Q}$. En introduisant le nombre d'oscillations ${\displaystyle n(t)=\omega _{0}t/2\pi }$, l'oscillation s'écrit pour β<1

${\displaystyle x=Ae^{-{\frac {\omega _{\circ }}{2Q}}t}\cos \varphi (t)=Ae^{-\pi {\frac {n(t)}{Q}}}\cos \varphi (t).}$

Ainsi, pour des oscillateurs peu amortis, le ${\displaystyle Q}$ est égal à π fois le nombre d'oscillations que le système fait pendant que son amplitude tombe d'un facteur ${\displaystyle 1}$/${\displaystyle e}$ ou à ${\displaystyle 3}$ fois le nombre d'oscillations pour que l'amplitude tombe à ${\displaystyle 1}$/${\displaystyle 3}$ si l'on tolère une approximation plus grossière.

Puisque l'énergie mécanique de l'oscillateur est proportionnelle au carré de l'amplitude, ${\displaystyle Q}$ est aussi égal à 2π fois le nombre d'oscillations effectuées avant que son énergie ne tombe d'un facteur ${\displaystyle 1}$/${\displaystyle e}$, ce qui revient à dire que ${\displaystyle Q}$ est aussi égal au nombre d'oscillations effectuées avant que son énergie ne tombe d'un facteur ${\displaystyle 1}$/${\displaystyle e^{2\pi }}$≈${\displaystyle 1}$/${\displaystyle 535}$.

Oscillations forcées

Généralités

Ces oscillations correspondent à une équation non homogène qui s'écrit

${\displaystyle M{\ddot {x}}+B{\dot {x}}+Kx=F\cos \omega t}$

Selon la théorie, la solution générale d'une telle équation est égale à la somme de la solution générale de l'équation homogène et d'une solution particulière de l'équation non homogène. Ceci se traduit en disant que le mouvement obtenu est la somme de l'oscillation propre, qui dépend des conditions initiales, et de l'oscillation forcée par la force extérieure ; on parle aussi de réponse à l'excitation décrite par le second membre. Généralement, il suffit de ne considérer que cette réponse qui subsiste seule après l'extinction de l'oscillation propre due à l'amortissement.

Pour ce faire il est commode d'utiliser les nombres complexes en considérant simultanément l'équation

${\displaystyle M{\ddot {y}}+B{\dot {y}}+Ky=F\sin \omega t}$

et d'ajouter cette équation multipliée par i à la précédente. En posant x + i y = z, on obtient

${\displaystyle M{\ddot {z}}+B{\dot {z}}+Kz=Fe^{i\omega t}}$

La recherche d'une solution ${\displaystyle z=Ze^{i\omega t}}$ conduit à

${\displaystyle (K-M\omega ^{2}+iB\omega )Z=F\,}$

En ignorant pour l'instant la forme exacte, cette équation se réécrit

${\displaystyle Z=H(\omega )F\,}$

H(ω) représente la fonction de transfert qui décrit la réponse en fonction de la pulsation. Elle peut s'exprimer en module et argument :

${\displaystyle H(\omega )=|H|e^{i\varphi }\,}$

d'où

${\displaystyle z=|H|F\,e^{i(\omega t+\varphi )}\,}$

La partie réelle est

${\displaystyle x=|H|F\,\cos(\omega t+\varphi )\,}$

Ainsi, à une excitation sinusoïdale un système linéaire fait correspondre une réponse sinusoïdale de même pulsation. De même, à une somme de sinusoïdes correspond une somme de sinusoïdes. Pour chacune d'entre elles le module et l'argument de la fonction de transfert représentent respectivement l'amplification et le déphasage. À l'inverse, toute non-linéarité crée des composantes qui n'existent pas dans l'excitation.

Systèmes conservatifs

La fonction de transfert s'écrit

${\displaystyle H(\omega )={1 \over {K-M\omega ^{2}}}}$

Son module est

${\displaystyle |H(\omega )|={1 \over |K-M\omega ^{2}|}}$

L'amplification croît avec un déphasage nul à partir de la valeur statique F/K jusqu'à l'infini lorsque ω atteint la valeur ω₀. Ensuite elle décroît jusqu'à zéro avec un déphasage égal à -π.

La valeur infinie correspond à la résonance lorsque le système est excité à sa pulsation propre. Dans la conception d'un système, le simple calcul de cette pulsation (ou fréquence ou période propre) peut conduire à modifier l'inertie ou la raideur d'un système pour l'éloigner des excitations attendues. En tout état de cause, la réponse ne peut être que finie à cause de l'amortissement qui est négligé ici.

Systèmes dissipatifs

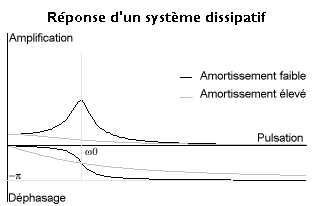
Dans ce système plus réaliste, la fonction de transfert devient

${\displaystyle H(\omega )={1 \over {K-M\omega ^{2}+iB\omega }}}$

L'amplification est

${\displaystyle |H|={1 \over {\sqrt {(K-M\omega ^{2})^{2}+B^{2}\omega ^{2}}}}}$

Il apparaît que le dénominateur de la fonction de transfert ne peut plus s'annuler : pour un amortissement faible on a une courbe de réponse voisine de celle du système non amorti mais avec un maximum fini. En annulant la dérivée de |H| par rapport à ω², on obtient la pulsation qui donne ce maximum :

${\displaystyle \omega ^{2}=\omega _{0}^{2}-{1 \over 2}\,\left({B \over M}\right)^{2}}$

À mesure que le coefficient d'amortissement B augmente, l'abscisse du maximum diminue jusqu'à 0 où la fonction de ω devient décroissante, ce qui se produit pour l'amortissement critique

${\displaystyle B_{\text{crit}}=2{\sqrt {K\,M}}\,}$

Le déphasage est défini par

${\displaystyle \cos \varphi =|H|(K-M\omega ^{2})\quad \sin \varphi =-|H|B\omega }$

Pour les plus petites valeurs de la pulsation on a le régime quasi statique dominé par la raideur dans lequel la réponse est en phase avec l'excitation ; pour les plus grandes, on atteint le régime dominé par l'inertie dans lequel la réponse est en opposition et l'amplification est de l'ordre de F/Mω². L'amortissement devient essentiel loin de ces deux extrêmes.

Facteur de qualité et oscillations forcées

Réponse en fréquence d'un système oscillant.

Dans le même exemple précédent on peut écrire la fonction de transfert comme:

${\displaystyle H(\omega )={1 \over K}{1 \over {1-{M \over K}\omega ^{2}+i{B \over K}\omega }}}$

avec ${\displaystyle \textstyle {\omega _{\circ }^{2}={K \over M}}}$ et ${\displaystyle \textstyle {{B \over K}={1 \over \omega _{\circ }Q}}}$.

Avec ceci, la fonction de transfert peut s'écrire:

${\displaystyle H(\omega )={1 \over K}{1 \over 1-\left({\omega \over \omega _{\circ }}\right)^{2}+i{1 \over Q}{\omega \over \omega _{\circ }}}}$

Le module de la fonction de transfert est:

${\displaystyle \left|H\right|={1 \over K}{1 \over {\sqrt {\left(1-\left({\omega \over \omega _{\circ }}\right)^{2}\right)^{2}+{1 \over Q^{2}}\left({\omega \over \omega _{\circ }}\right)^{2}}}}}$

En observant les courbes de droite on comprend mieux l'intérêt d'utiliser le facteur de qualité ${\displaystyle Q}$. L'amplitude à la résonance est ${\displaystyle Q}$ fois l'amplitude en basse fréquence.

Articles connexes

• Oscillateur harmonique
• Système mécanique linéaire pour quelques remarques plus générales.
• Analogie électro-mécanique synthétise les grandeurs analogues entre oscillateurs mécaniques et électriques
• Système dynamique
• Théorie du chaos

Bibliographie

• Vladimir Damgov, Nonlinear and parametric phenomena. Applications to radiometric and mechanical systems, World Scientific, Series on Nonlinear Sciences, 2004.

• Portail de l'analyse
• Portail de la physique